Процедура преобразования двоичного числа в десятичное проста: необходимо сложить десятичные веса всех разрядов двоичного числа, в которых содержатся единицы.
Пример 1. Преобразование целого двоичного числа 11001100 в десятичное:
|







 1 1 0 0 1 1 0 0
1 1 0 0 1 1 0 0
 | |||||||||||
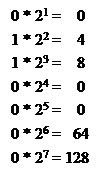 | |||||||||||
 | |||||||||||
 | |||||||||||
 | |||||||||||
 | |||||||||||
 | |||||||||||
 | |||||||||||
 | |||||||||||
∑ 204
Результат. 11001100 дв. = 204 дес.
Пример 2. Преобразование вещественного двоичного числа 101.011 в десятичное.





 1 0 1. 0 1 1
1 0 1. 0 1 1
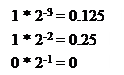 | ||||||||||
 | ||||||||||
 | ||||||||||
 | ||||||||||
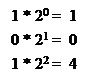 | ||||||||||
 | ||||||||||
 | ||||||||||
 | ||||||||||
∑ 5.375
Результат. 101.011 дв. = 5,375 дес.
Шестнадцатеричная система счисления.
В шестнадцатеричной системе счисления используются следующие 16 символов: 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F. Практическое использование шестнадцатеричной системы счисления объясняется тем, что число 16 есть число 2 в четвертой степени. Иначе говоря, шестнадцатеричную цифру можно использовать как средства сокращенной записи 4-разрядного двоичного числа. Процедура преобразования двоичного числа в шестнадцатеричное довольно проста. Биты, начиная с младшего значащего бита (расположенного рядом с двоичной точкой), объединяются в группы по четыре. Каждой группе подбирается соответствующий шестнадцатеричный символ.
Чтобы преобразовать двоичное число 10101011111101, необходимо сформировать биты в группы по четыре, начиная справа, и добавить два незначащих нуля в левую крайнюю группу для формирования четырех бит: 0010 1010 1111 1101. Заменим каждую группу битов соответствующим шестнадцатеричным символом, получим число 2AFD.

 Принято шестнадцатеричные числа обозначать в конце числа большой латинской буквой H. Например: 2AFDH, C7H, 3H, 5AH и т. п.
Принято шестнадцатеричные числа обозначать в конце числа большой латинской буквой H. Например: 2AFDH, C7H, 3H, 5AH и т. п.
Следует помнить, что шестнадцатеричные числа - это только способ представления двоичных чисел, которыми фактически оперирует микропроцессор.
Шестнадцатеричные числа и их двоичные и десятичные эквиваленты.
| Шестнадцате-ричное число | Двоичное число | Десятичное число |
0 0 0
1 1 1
2 10 2
3 11 3
4 100 4
5 101 5
6 110 6
7 111 7
8 1000 8
9 1001 9
A 1010 10
B 1011 11
C 1100 12
D 1101 13
E 1110 14
F 1111 15
10 1 0000 16
11 1 0001 17
12 1 0010 18
13 1 0011 19
14 1 0100 20
15 1 0101 21
16 1 0110 22
17 1 0111 23
18 1 1000 24
19 1 1001 25
1A 1 1010 26
1B 1 1011 27
1C 1 1100 28
1D 1 1101 29
1E 1 1110 30
1F 1 1111 31
20 10 0000 32
ДВОИЧНАЯ АРИФМЕТИКА
Двоичное сложение.
Сложение двоичных чисел подобно сложению десятичных. В обоих случаях операции начинаются с обработки наименьших значащих цифр, расположенных в крайней справа позиции. Если результат сложения наименьших значащих цифр двух слагаемых не помещается в соответствующем разряде результата, то происходит перенос. Цифра, переносимая в соседний слева разряд, добавляется к содержимому последнего. Сложение цифр любых одноименных разрядов может повлечь за собой перенос в более старший разряд. Перенос возникает, если результат сложения цифр одноименных разрядов больше 9 при использовании десятичной арифметики, и больше 1 в случае двоичной системы.
Сходство и различие операций десятичного и двоичного сложения можно продемонстрировать на следующем примере:
Десятичная Двоичная
Слагаемое 1 99 0110 0011
Слагаемое 2 95 0101 1111
------------------------------- ---------------
Сумма 194 1100 0010
Рассмотренный пример свидетельствует о простоте процедуры двоичного сложения. Единственное неудобство, присущее двоичным операциям, - громоздкость записи больших чисел в двоичной форме, что вызывает множество переносов из одного разряда в другой при выполнении операции сложения.
Двоичное вычитание.
Двоичное вычитание подобно десятичному вычитанию. Как и в случае сложения, различие выполнения вычитания в двоичной и десятичной форме состоит лишь в особенностях поразрядных операций.
Сравнение процедур десятичного и двоичного вычитания можно продемонстрировать на следующем примере:
Десятичная Двоичная
Уменьшаемое 109 0110 1101
Вычитаемое 49 0011 0001
------------------------------ -------------
Разность 60 0011 1100
Двоичное вычитание начинается операцией над значением крайних справа двоичных разрядов уменьшаемого и вычитаемого.
Двоичное умножение.
Двоичное и десятичное умножение, так же, как и двоичное и десятичное сложение или вычитание, во многом похожи. Умножение - это быстрый способ сложения нескольких одинаковых чисел. При умножении одно из чисел называется множимым, другое - множителем. Умножение выполняется поразрядно.
Создан простой способ выполнения двоичного умножения, получивший название "умножение путем сдвига и сложения". Перечислим основные правила этого способа.
1. Формирование первого частичного произведения.
Если значение младшего значащего разряда множителя равно 0, то и результат равен 0, если значение этого разряда равно 1, то результат является копией множимого.
2. Правило сдвига.
При использовании очередного разряда множителя для формирования частичного произведения производится сдвиг множимого на один разряд (позицию) влево.
3. Правило сложения.
Каждый раз, когда значение разряда множителя равно 1, к результату необходимо прибавить множимое, расположенное в позиции, определенной правилом сдвига.
4. Определение результирующего произведения.
Искомое произведение есть результат выполнения всех операций сдвига и сложения.
Продемонстрируем действие этого способа на примере умножения 17 на 11.
Десятичная Двоичная
Множимое 17 0001 0001
Множитель 11 0000 1011
-------------
--------------------------- -----------------
Произведение 187 00010111011
Двоичное деление.
Деление - это операция, обратная умножению. Иначе говоря, при делении операцию вычитания повторяют до тех пор, пока уменьшаемое не станет меньше вычитаемого. Число этих повторений показывает, сколько раз вычитаемое укладывается в уменьшаемом.
Варианты контрольных заданий.
| № пп | Двоичная арифметика | Минимизация переключ. функций | Счетчики | Примечание |
| 1.1 | 2.1 | 3.1 | ||
| 1.2 | 2.2 | 3.2 | ||
| 1.3 | 2.3 | 3.3 | ||
| 1.4 | 2.4 | 3.4 | ||
| 1.5 | 2.5 | 3.5 | ||
| 1.6 | 2.6 | 3.6 | ||
| 1.7 | 2.7 | 3.7 | ||
| 1.8 | 2.8 | 3.8 | ||
| 1.1 | 2.8 | 3.1 | ||
| 1.2 | 2.7 | 3.2 | ||
| 1.3 | 2.6 | 3.3 | ||
| 1.4 | 2.5 | 3.4 | ||
| 1.5 | 2.4 | 3.5 | ||
| 1.6 | 2.3 | 3.6 | ||
| 1.7 | 2.2 | 3.7 | ||
| 1.8 | 2.1 | 3.8 | ||
| 1.1 | 2.8 | 3.8 | ||
| 1.2 | 2.7 | 3.7 | ||
| 1.3 | 2.6 | 3.6 | ||
| 1.4 | 2.5 | 3.5 | ||
| 1.5 | 2.4 | 3.4 | ||
| 1.6 | 2.3 | 3.3 | ||
| 1.7 | 2.2 | 3.2 | ||
| 1.8 | 2.1 | 3.1 | ||
| 1.1 | 2.1 | 3.8 | ||
| 1.2 | 2.2 | 3.7 | ||
| 1.3 | 2.3 | 3.6 | ||
| 1.4 | 2.4 | 3.5 | ||
| 1.5 | 2.5 | 3.4 | ||
| 1.6 | 2.6 | 3.3 | ||
| 1.7 | 2.7 | 3.2 | ||
| 1.8 | 2.8 | 3.1 | ||
| 1.8 | 2.1 | 3.8 | ||
| 1.7 | 2.2 | 3.7 | ||
| 1.6 | 2.3 | 3.6 | ||
| 1.5 | 2.4 | 3.5 | ||
| 1.4 | 2.5 | 3.4 | ||
| 1.3 | 2.6 | 3.3 | ||
| 1.2 | 2.7 | 3.2 | ||
| 1.1 | 2.8 | 3.1 |
Контрольные задания
1. Двоичная арифметика.
1.1. Представить в двоичной системе счисления и сложить два числа: 97 и 115. Результат представить в шестнадцатиричной системе счисления.
1.2. Представить в двоичной системе счисления и сложить два числа: 83 и 126. Результат представить в шестнадцатиричной системе счисления.
1.3. Представить в двоичной системе счисления и умножить два числа: 97 и 5. Результат представить в шестнадцатиричной системе счисления.
1.4. Представить в двоичной системе счисления и умножить два числа: 9 и 15. Результат представить в шестнадцатиричной системе счисления.
1.5. Представить в двоичной системе счисления и умножить два числа: 6 и 35. Результат представить в шестнадцатиричной системе счисления.
1.6. Сложить числа, представленные в шестнадцатиричной системе счисления: 3F и AD. Результат представить в десятичной системе счисления.
1.7. Сложить числа, представленные в шестнадцатиричной системе счисления: 6A и 7C. Результат представить в десятичной системе счисления.
1.8. Сложить дробные числа, представленные в двоичной системе счисления 1100,1011 и 1001,1001. Результат представить в десятичной системе счисления.