1. 
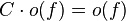
2. 
как следствия:
3. 
4. 
5. 
Свойство 1 и 2
Пусть 
и 
– бесконечно малые функции при х 
а.
= о(β) и = о(β)
+ = о(β)
= о(β) т.е. 
= о(β) т.е. 
__________________________________________________________________
Свойство 3
α= о(Сβ) 
, С 
0, С=о(β)-?
;( 
Умножение и деление на С 
__________________________________________________________________
Свойство 4
C 
; 
Свойство 5
о( 
, n 
); 
)) -?
;( 
= 
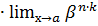=o 
=o
__________________________________________________________________
Свойство 6
(o( 
=o( 
n 
N
Пример:
(предположим sinx= o( 
, 0<t<1
= 
= 
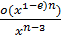= =св-во 8=o( 
( 
__________________________________________________________________
Свойство
=o(
__________________________________________________________________
Свойство
= 0
__________________________________________________________________
Свойство
o(o( 
; 
; 
__________________________________________________________________
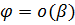
Свойство
o(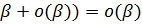 
+ 
__________________________________________________________________
Свойство
__________________________________________________________________
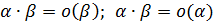
Свойство
__________________________________________________________________
Cвойства «O – большое»
Свойство
O(o(f(x))=o(f(x))
µ(x) = O(o(f(x)), g(x) = o(f)
__________________________________________________________________
Свойство
o(O(f)x))) = o(f(x))
g(x)=O(f(x)) 
,
__________________________________________________________________
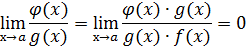
Свойство
O(o(f(x)) = O(f(x)
g(x)=O(f(x))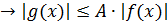 
__________________________________________________________________
Свойство
O(f(x)) + o(f(x) – O(f(x))
g(x) = o(f(x) = 0 
__________________________________________________________________
Пример:
1)Sinx-x=o(x) -?
2) cos x – 1 + 
Асимптотические обозначения в уравнениях
· Если в правой части уравнения находится только асимптотическое обозначение (например n = O (n ²)), то знак равенства обозначает принадлежность множеству (n ∈ O (n ²)).
· Если в уравнении асимптотические обозначения встречается в другой ситуации, они рассматриваются как подставляемые взамен их некоторые функции. Например, при x → 0 формула 
обозначает, что 
, где 
— функция, о которой известно только то, что она принадлежит множеству 
. Предполагается, что таких функций в выражении столько, сколько раз встречаются в нём асимптотические обозначения. Например, 
— содержит только одну функцию из класса 
.
· Если асимптотические обозначения встречаются в левой части уравнения, используют следующее правило:
какие бы мы функции ни выбрали (в соответствии с предыдущим правилом) взамен асимптотических обозначений в левой части уравнения, можно выбрать функции вместо асимптотических обозначений (в соответствии с предыдущим правилом) в правой части так, что уравнение будет правильным.
Например, запись 
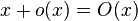обозначает, что для любой функции, существует некоторая функция g(x) 
такая, что выражение x+ f(x) = g(x) — верно для всех 
.
· Несколько таких уравнений могут быть объединены в цепочки. Каждое из уравнений в таком случае следует интерпретировать в соответствии с правилом.
Например: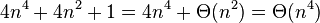 
. Отметим, что такая интерпретация подразумевает выполнение соотношения 
.
Приведенная интерпретация подразумевает выполнение соотношения:
, где A, B, C — выражения, которые могут содержать асимптотические обозначения.
Примеры использования: 
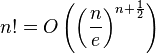при 
при 
(следует из формулы Стирлинга: 
Формула Стирлинга является первым приближением при разложении факториала в ряд Стирлинга: 
при .
При 
выполнено неравенство 
.
Поэтому положим 
.
Отметим, что нельзя положить 
, так как 
и, следовательно, это значение при любой константе 
больше 
.
Функция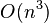 
при имеет степень роста.
Чтобы это показать, надо положить и 
. Можно, конечно, сказать, что 
имеет порядок 
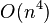, но это более слабое утверждение, чем то, что 
.
Докажем, что функция 
при не может иметь порядок 
.
Предположим, что существуют константы и 
такие, что для всех 
выполняется неравенство 
.
Тогда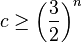 
для всех . Но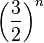 
принимает любое, как угодно большое, значение при достаточно большом 
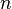, поэтому не существует такой константы , которая могла бы мажорировать 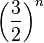для всех 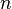больших некоторого .
.
Для проверки достаточно положить 
. Тогда 
для 
Литература
· В. Н. Крупский Введение в сложность вычислений.
· Бугров, Никольский Высшая математика, том 2.
- https://ru.wikipedia.org/wiki/%C2%ABO%C2%BB_%D0%B1%D0%BE%D0%BB%D1%8C%D1%88%D0%BE%D0%B5_%D0%B8_%C2%ABo%C2%BB_%D0%BC%D0%B0%D0%BB%D0%BE%D0%B5
- https://ru.math.wikia.com/wiki/%C2%ABO%C2%BB_%D0%B1%D0%BE%D0%BB%D1%8C%D1%88%D0%BE%D0%B5_%D0%B8_%C2%ABo%C2%BB_%D0%BC%D0%B0%D0%BB%D0%BE%D0%B5