Векторная алгебра. Нелинейные операции над векторами.
3.1.Понятие вектора и линейные операции над векторами.
3.2.Линейная зависимость векторов. Базис на плоскости и в пространстве.
3.3.Нелинейные операции над векторами.
Понятие вектора и линейные операции над векторами.
Опр.1 Вектором называется направленный отрезок, имеющий определенную длину.
Опр.2 Длиной вектора  называется его модуль и обозначается символом
называется его модуль и обозначается символом  . Модуль вектора
. Модуль вектора  обозначается
обозначается  .
.
Опр.3 Вектор называется единичным, если его длина равна единице, т.е.  . Вектор называется нуль - вектором, если его длина равна нулю, т.е.
. Вектор называется нуль - вектором, если его длина равна нулю, т.е.  , обозначается
, обозначается  (нуль – вектор не имеет направления, его начало и конец совпадают).
(нуль – вектор не имеет направления, его начало и конец совпадают).
Опр.4 Два вектора называются коллинеарными, если они лежат на одной прямой или параллельных прямых, в противном случае вектора – неколлинеарные. Три вектора называются компланарными, если они лежат в одной плоскости или параллельны одной плоскости, в противном случае вектора – некомпланарными.
Опр.5 Два вектора называются равными, если они коллинеарные, одинаково направленные и имеют одинаковую длину, записывают  .
.
Опр.6 Вектор, образованный из данного вектора параллельным переносом, называется свободным.
Линейные операции над векторами. Линейными операциями называются операции сложения векторов, вычитания векторов и умножение вектора на число.
Опр.7 Суммой нескольких векторов называется вектор, по величине и направлению равный замыкающей ломаной линии, построенной на свободных векторах, соответствующих данным векторам, его начало совпадает с налом первого, а конец с концом последнего.
Свойства суммы векторов.
Сумма конечного числа векторов обладает переместительным и сочетательным законом.
Опр.8 Сумму двух векторов можно найти по правилу треугольника или правилу параллелограмма.
Опр.9 Под разностью двух векторов 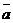 и
и 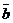 понимают вектор
понимают вектор 
 такой, что
такой, что 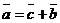 (разность двух векторов можно найти по правилу треугольника или правилу параллелограмма).
(разность двух векторов можно найти по правилу треугольника или правилу параллелограмма).
Опр.10 Произведением вектора 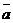 на скаляр
на скаляр  называют вектор
называют вектор 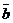 =
=  , длина которого равна
, длина которого равна  и направление: совпадает с направлением вектора
и направление: совпадает с направлением вектора 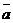 , если
, если  ; противоположно направлению вектора
; противоположно направлению вектора 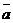 , если
, если  . Вектор
. Вектор 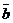 =
=  , если
, если  .
.
Линейная зависимость векторов. Базис на плоскости и в пространстве.
Опр.11 Векторы  называются линейно зависимыми, если существуют числа
называются линейно зависимыми, если существуют числа 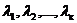 не все равные нулю, для которых имеет место равенство
не все равные нулю, для которых имеет место равенство  и если
и если  , то векторы называются линейно независимыми.
, то векторы называются линейно независимыми.
Опр.12 Если вектора  линейно зависимы и, предположим
линейно зависимы и, предположим  , то его можно представить в виде линейной комбинации остальных векторов
, то его можно представить в виде линейной комбинации остальных векторов  и эти векторы называют базисом, а числа
и эти векторы называют базисом, а числа  - координатами вектора
- координатами вектора 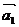 и обозначают
и обозначают  .
.
Свойства линейной зависимости векторов.
Свойство 1. Если вектора  линейно зависимы, то хотя бы один можно представить в виде линейной комбинации других.
линейно зависимы, то хотя бы один можно представить в виде линейной комбинации других.
Свойство 2. Если один из векторов  представлен в виде линейной комбинации других векторов, то все эти вектора
представлен в виде линейной комбинации других векторов, то все эти вектора  линейно зависимы.
линейно зависимы.
Теорема 1. Всякие три вектора на плоскости линейно зависимы.
Следствие 1. Если на плоскости дано более трех векторов, то они линейно зависимы.
Теорема 2. Для того чтобы два вектора были на плоскости линейно независимыми необходимо и достаточно, чтобы они были неколлинеарными.
Следствие 2. Максимальное число линейно независимых векторов на плоскости два.
Теорема 3. Всякие четыре вектора в пространстве линейно зависимы.
Следствие 1. Если в пространстве дано более четырех векторов, то они линейно зависимы.
Теорема 4. Для того чтобы три вектора были в пространстве линейно независимыми необходимо и достаточно, чтобы они были некомпланарными.
Следствие 4. Максимальное число линейно независимых векторов в пространстве три.
Опр.13 Базисом на плоскости называются два любых линейно независимых вектора. Если 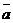 и
и 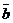 - базисные векторы плоскости,
- базисные векторы плоскости,  - любой вектор плоскости, тогда
- любой вектор плоскости, тогда 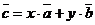 - выражается через базисные векторы, а если какой – либо вектор
- выражается через базисные векторы, а если какой – либо вектор  представлен в виде
представлен в виде 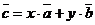 , то говорят, что он разложен по базису и в данном базисе имеет координаты
, то говорят, что он разложен по базису и в данном базисе имеет координаты  .
.
Теорема 5. Разложение вектора  по базису
по базису 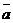 и
и 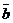 является единственным.
является единственным.
Опр.14 В декартовой прямоугольной системе координат базисные векторы на плоскости обозначаются 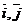 и данные векторы единичные, взаимно перпендикулярные.
и данные векторы единичные, взаимно перпендикулярные.
Опр.15 Базисом в пространстве называются три любых линейно независимых вектора. Если 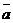 ,
, 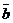 ,
,  - базисные векторы пространства,
- базисные векторы пространства,  - любой вектор пространства, тогда
- любой вектор пространства, тогда  - выражается через базисные векторы, а если какой – либо вектор
- выражается через базисные векторы, а если какой – либо вектор  представлен в виде
представлен в виде  , то говорят, что он разложен по базису и в данном базисе имеет координаты
, то говорят, что он разложен по базису и в данном базисе имеет координаты  .
.
Теорема 6. Разложение вектора  по базису
по базису 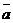 ,
, 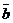 ,
,  является единственным.
является единственным.
Опр.16 В декартовой прямоугольной системе координат базисные векторы в пространстве обозначаются  и данные векторы единичные, взаимно перпендикулярные.
и данные векторы единичные, взаимно перпендикулярные.
Длина вектора, линейные операции с векторами, заданными в координатной форме. Пусть вектора  и
и  разложены по базису и представлены в виде
разложены по базису и представлены в виде  и
и  тогда:
тогда:
длина вектора находится по формуле  ;
;
сумма векторов находится по формуле  =
=  ;
;
разность векторов находится по формуле  =
=  ;
;
умножение вектора на число находится по формуле 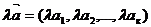 .
.
Теорема 7. Если несколько векторов образуют базис, то определитель построенный на их координатах отличен от нуля.