Функциональные ряды
Равномерная сходимость функционального ряда
Пусть  – функции комплексной переменной z. Ряд
– функции комплексной переменной z. Ряд

носит название функционального ряда.
Важнейшим понятием для теории таких рядов является понятие равномерной сходимости.
Пусть сказано «функциональный ряд сходится в области G ». Что это значит? Это значит, что он сходится в каждой точке этой области, то есть
 .
.
Самым неприятным является тут то, что  зависит не только от e, но и от z. Из-за этой зависимости ряд может иметь очень неприятные свойства. Желание избавится от z и приводит к понятию равномерной сходимости функционального ряда.
зависит не только от e, но и от z. Из-за этой зависимости ряд может иметь очень неприятные свойства. Желание избавится от z и приводит к понятию равномерной сходимости функционального ряда.
Определение. Говорят, что функциональный ряд сходится равномерно в области G, если
 .
.
Обратите внимание на то, куда переместился квантор 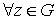 и на то, что теперь
и на то, что теперь  зависит только от e.
зависит только от e.
Равномерно сходящиеся ряды обладают очень хорошими свойствами, которые будут описаны ниже.
Признак Вейерштрасса. Если существуют такие неотрицательные числа  , что
, что
1.  ,
,  ;
;
2. 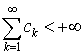 ,
,
то ряд  сходится равномерно в области G.
сходится равномерно в области G.
Свойства равномерно сходящихся функциональных рядов
Не давая точных формулировок, перечислим свойства равномерно сходящихся функциональных рядов.
1. Если все 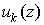 непрерывны в области G, то сумма ряда
непрерывны в области G, то сумма ряда  есть также непрерывная области G функция.
есть также непрерывная области G функция.
2. Если все 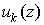 аналитичны в области G, то сумма ряда
аналитичны в области G, то сумма ряда  есть также аналитическая в области G функция.
есть также аналитическая в области G функция.
3. Если ряд  сходится равномерно в области G, то в нем допустим почленный переход к пределу, то есть
сходится равномерно в области G, то в нем допустим почленный переход к пределу, то есть
 .
.
4. Если ряд  сходится равномерно в области G, то его можно почленно интегрировать, то есть
сходится равномерно в области G, то его можно почленно интегрировать, то есть
 .
.
5. Если ряд  сходится равномерно в области G, то его можно почленно дифференцировать любое число раз, то есть
сходится равномерно в области G, то его можно почленно дифференцировать любое число раз, то есть
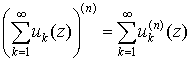 .
.
Определение степенного ряда. Теорема Абеля
Степенные ряды являются частным случаем функциональных рядов.
Определение. Степенным рядом называется функциональный ряд вида  .(1.1)
.(1.1)
Здесь  – постоянные вещественные числа, называемые коэффициентами степенного ряда; а – некоторое постоянное число, х – переменная, принимающая значения из множества действительных чисел.
– постоянные вещественные числа, называемые коэффициентами степенного ряда; а – некоторое постоянное число, х – переменная, принимающая значения из множества действительных чисел.
При  степенной ряд (1.1) принимает вид
степенной ряд (1.1) принимает вид
 . (1.2)
. (1.2)
Степенной ряд (1.1) называют рядом по степеням разности  ,
,
ряд (1.2) – рядом по степеням х.
Если переменной х придать какое-либо значение, то степенной ряд (1.1) (или (1.2)) превращается в числовой ряд, который может сходиться или расходиться.
Определение. Областью сходимости степенного ряда называется множество тех значений х, при которых степенной ряд сходится.
Ряд (1.1) с помощью подстановки  приводится к более простому виду (1.2), поэтому вначале будем рассматривать степенные ряды вида (1.2).
приводится к более простому виду (1.2), поэтому вначале будем рассматривать степенные ряды вида (1.2).
Для нахождения области сходимости степенного ряда важную роль играет следующая теорема.
Теорема Абеля:
если степенной ряд (1.2) сходится при  , то он абсолютно сходится при всех значениях х, удовлетворяющих неравенству
, то он абсолютно сходится при всех значениях х, удовлетворяющих неравенству  ; если же ряд (1.2) расходится при
; если же ряд (1.2) расходится при  , то он расходится при всех значениях х, удовлетворяющих неравенству
, то он расходится при всех значениях х, удовлетворяющих неравенству  .
.
Теорема Абеля дает ясное представление о структуре области сходимости степенного ряда.
область сходимости степенного ряда (1.2) совпадает с одним из следующих интервалов: 1)  ; 2)
; 2)  ; 3)
; 3) 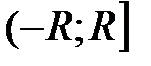 ; 4)
; 4)  ,
,
где R – некоторое неотрицательное действительное число или 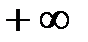 .
.
Число R называется радиусом сходимости, интервал  – интервалом сходимости степенного ряда (1.2).
– интервалом сходимости степенного ряда (1.2).
Если  , то интервал сходимости представляет собой всю числовую ось
, то интервал сходимости представляет собой всю числовую ось  .
.
Если  , то интервал сходимости вырождается в точку
, то интервал сходимости вырождается в точку 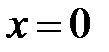 .
.
Замечание: если  – интервал сходимости для степенного ряда (1.2),
– интервал сходимости для степенного ряда (1.2),
то  – интервал сходимости для степенного ряда (1.1).
– интервал сходимости для степенного ряда (1.1).
Для практического нахождения области сходимости степенного ряда (1.2) достаточно найти его радиус сходимости R и выяснить вопрос о сходимости этого ряда на концах интервала сходимости  , т. е. при
, т. е. при  и
и  .
.
Радиус сходимости R степенного ряда можно найти по одной из следующих формул:
формула Даламбера:  ;(1.3)
;(1.3)
формула Коши:  .(1.4)
.(1.4)
Если в формуле Коши  , то полагают
, то полагают  , если
, если 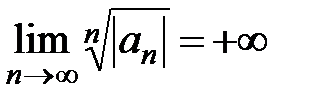 , то полагают
, то полагают  .
.