Лекции 10. Синтез БИХ-фильтров
1. Синтез БИХ-фильтров на основе АФП.
2. Метод инвариантности импульсной характеристики.
3. Процедура синтеза БИХ-фильтра методом инвариантности импульсной характеристики.
4. Метод билинейного Z-преобразования.
5. Свойства билинейного Z-преобразования.
6. Процедура синтеза оптимального БИХ-фильтра методом билинейного Z-преобразования.
10.1. Синтез БИХ-фильтров на основе АФП
Синтез БИХ-фильтров на основе аналоговых фильтров-прототипов (АФП) основан на том, что передаточные функции БИХ-фильтра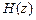 
и АФП 
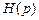имеют одинаковое математическое представление в виде
а также ее разновидности в виде:
1..
2.
Передаточная функция БИХ-фильтра общего вида:
.
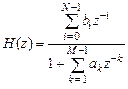Порядок БИХ-фильтра равен порядку передаточной функции.
Разновидности АФП по типу аппроксимации определяют типы АФП (рис. 10.1):
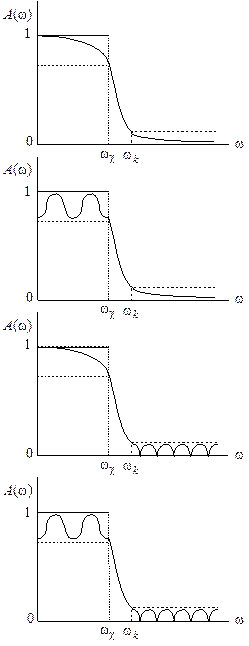
Рис. 10.1. Приблизительный вид АЧХ АФП (для ФНЧ): Баттерворта; Чебышева 1-го рода; Чебышева 2-го рода; Золотарева-Кауэра
Далее, с целью противопоставления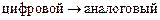 
, будем говорить ЦФ, подразумевая БИХ-фильтр, и АФП.
Рассмотрим два метода синтеза ЦФ на основе АФП.
10.2. Метод инвариантности импульсной характеристики
Постановка задачи: синтезировать ЦФ, ИХ которого совпадает с ИХ АФП в дискретных точках (рис. 10.2):
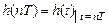. (10.1)
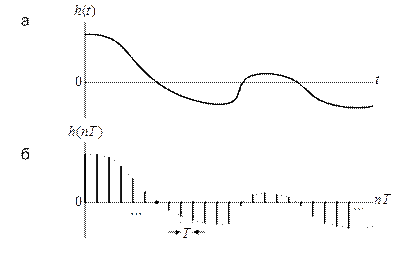
Рис. 10.2. Импульсная характеристика: АФП (а); ЦФ (б)
Решение задачи
Требуется: выразить параметры 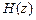ЦФ через параметры 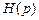АФП.
Передаточная функция ЦФ связана с ИХ
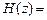(10.2)
ИХ АФП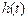 
связана с его передаточной функцией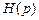
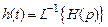. (10.3)
Представим 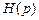в виде
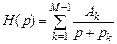. (10.4)
где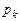 
— 
—
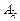Получим ИХ АФП, используя свойство
.
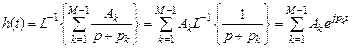Заменяя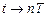 
, получим ИХ ЦФ:
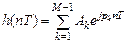. (10.5)
Получим ИХ ЦФ на основе (10.) и (10.):
.
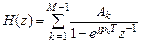. (10.6)
АЧХ ЦФ
В этом методе используется стандартное Z -преобразование.
Ось частот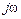 
p -плоскости отображается на z -плоскость в
Следовательно, ЧХ ЦФ представляет собой периодическое продолжение ЧХ ЦФ с периодом
Графики АЧХ АФП и АЧХ ЦФ ФНЧ имеют вид:
Выводы:
1. АЧХ ЦФ имеет на границе
Для уменьшения можно:
· увеличить
· увеличить
Следовательно, метод инвариантности импульсной характеристики не позволяет синтезировать
2. Метод не рекомендуется использовать для синтеза
3. Соотношение между частотами АФП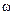 
и ЦФ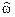 
—
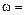
10.3. Процедура синтеза БИХ-фильтра методом инвариантности импульсной характеристики
1. Задание требований к АЧХ ЦФ.
2. Переход к требованиям к АЧХ АФП.
Правая граница основной полосы АЧХ ЦФ для АЧХ АФП соответствует
3. Выбор типа аппроксимации (типа АФП и ЦФ).
4. Синтез АФП — расчет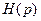 
в виде
5. Синтез ЦФ — расчет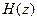 
по формуле (10.) в виде
6. Представление 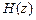в виде
что соответствует структуре БИХ-фильтра.
Метод билинейного Z-преобразования
Оптимальным БИХ-фильтром называют БИХ-фильтрминимального порядка при заданных требованиях к АЧХ.
Теоретические основы метода
В стандартном Z -преобразовании переменные z и p связаны соотношением:
.
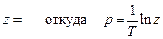Разложим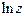 
в ряд Тейлора:
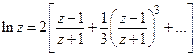
и возьмем один член ряда и получим формулу билинейного Z-преобразования:
, (10.7)
где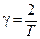 
.
Формула (10.7) называется формулой билинейного Z-преобразования.
Из (10.7) имеем:
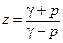. (10.8)
Передаточная функция ЦФ связана с передаточной функцией АФП соотношением:
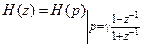
Свойства билинейного Z-преобразования
Ранее было рассмотрено отображение p -плоскости на z -плоскость для статарного Z-преобразования, когда
ü ось частот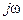 
p -плоскости на z -плоскости отображалась в…
ü левая p -полуплоскость на z -плоскости отображалась в…
ü нормированная частота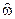 
ЦФ связана с частотой 
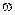АФП…
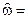
Сравним свойства билинейного Z-преобразовании со свойствами стандартного Z-преобразования.
Во избежание путаницы обозначим частоту АФП как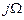 
.
1. Ось частот p -плоскости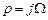 
.
По формуле (10.):
,
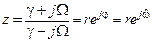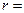
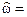(10.9)
|
|
| |
|
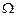
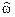
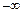
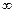
Выводы:
· Ось частот 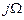отображается
· Бесконечная ось 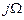сжимается в конечный отрезок длины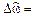 
· Бесконечная АЧХ АФП сжимается в АЧХ ЦФ конечной длины (отсутствует) и периодически продолжается с периодом
Графики АЧХ АФП и АЧХ ЦФ ФНЧ имеют вид:
2. Левая p -полуплоскость: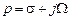 
, 
:
,
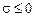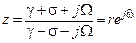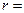
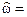
Вывод: левая p -полуплоскость отображается
3. Соотношение между частотами АФП 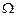и ЦФ —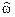
(см. (10.9) и рис. 10.3):
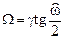. (10.10)
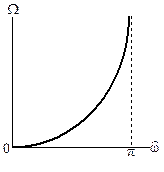
Рис. 10.3. Соотношение между частотами АФП и ЦФ