Этап 1. Распределение затрат на ресурсы

Для того чтобы рассчитать стоимость ресурсов, необходимо:

- вначале определить структуру ресурсов, а также перечень затрат, направляемых на обеспечение деятельности каждого ресурса,

- распределить затраты на ресурсы.

Как правило, выделяют следующие виды ресурсов:

- персонал;

- оборудование;

- транспорт;

, энергия, природные ресурсы;

- материалы и комплектующие;

- топливо помещения (земля).

Стоимость ресурсов «Материалы и комплектующие» и «Топливо, энергия, природные ресурсы», а также «Помещения (земля)», как правило, переносится на стоимость ресурсов «Персонал» или «Обо­рудование» в зависимости от того, для кого (чего) они постоянно ис­пользуются.

После того как перечень ресурсов сЬставлен, нужно распределить на них косвенные затраты. В большинстве случаев затраты однознач­но переносятся на ресурсы, например, сумма заработной платы ком­мерческого директора относится на ресурс «Коммерческий дирек­тор». Однако часто один вид затрат может переноситься на несколько ресурсов. Например, арендная плата офисных помещений должна быть разнесена на стоимость ресурсов из группы «Сотрудники», чьи рабочие места находятся в данном помещении.

Для переноса затрат на ресурсы используется драйвер затрат. Сначала определяется стоимость единицы драйвера затрат (для помещения, например, это стоимость аренды или эксплуатации 1 кв. м.), а затем сумма затрат, переносимая на данный ресурс, рассчитывается

Этап 2. Перенесение стоимости ресурсов на процессы (операции)

Стоимость ресурсов переносится на процессы (операции) пропорционально драйверам ресурсов. Чаще всего используют такие драйверы, как рабочие часы (для персонала) и машинное время (для оборудования). Определив стоимость использоваия единицы драйвера ресурсов (стоимость одного часа работы сотрудника, оборудования) и количество единиц драйвера, потребляемых каждым процессом (операцией), можно рассчитать стоимость данного ресурса, переносимую на конкретный процесс (операцию).

Этап 3. Распределение стоимости основных операций на объекты затрат

На последнем этапе стоимость основных процессов (операций) распределяется на объекты затрат. По аналогии с предыдущими этапами это распределение осуществляется пропорционально драйверам. В качестве драйверов операций выступают количественные характеристики самих объектов затрат, например, объем продаж или объем производства в денежном или натуральном выражении.

Объекты затрат могут быть различными, так как каждая организация выбирает их самостоятельно исходя из своих целей. На практике наиболее распространенными объектами затрат являются «Покупатели» или «Каналы

 

Статистические методы управления качеством.

Цель занятия – изучить основные методы управления качеством продукции и качеством управления организацией на основе математической статистики.

Современный менеджмент, как известно, является математическим, и для реализации цикла управления Шухарта – Деминга PDCA требует использования математических методов и математических моделей практически на всех этапах.

Одним из важнейших условий этого является овладение менеджерами всех звеньев статистическим мышлением. Под статистическим мышлением понимается подход к принятию управленческих решений на всех уровнях организации, причем как оперативных или тактических, так и стратегических. С татистическое мышление - это вовсе не простое использование статистических методов, или, по крайней мере, это не обязательное их использование. Это точка зрения, позиция, взгляд на мир, помогающие принимать эффективные решения благодаря системному подходу к возникающим проблемам. Очевидна важность этой позиции, ибо если мы вмешиваемся в процесс, когда этого делать не надо, или не вмешиваемся, когда это крайне важно, то процесс только ухудшается. Аналогичный результат возникает, если в процесс вмешиваются не те люди, кому следует это делать.

Поводом для возникновения статистического мышления послужила практическая задача борьбы с дефектами продукции, которая была поставлена перед молодым физиком Уолтером Шухартом, принятым в 1923 году на работу в знаменитую телефонную компанию Bell Laboratories. Задача эта была связана с одной трудностью, возникшей в ходе телефонизации Америки. При тогдашней технологии прокладки телефонных сетей приходилось примерно через каждые 500 м вставлять в линию связи усилительную подстанцию размером с письменный стол (полупроводники еще не вошли в жизнь), закапывая ее в землю. И все было бы хорошо, если бы не одно обстоятельство. Лампы в этих усилителях перегорали не по графику, а когда им вздумается. Из-за этого у бригад ремонтников возникали большие трудности. Не удавалось заранее определить требуемое число ремонтных бригад, их потребности в транспорте и запасах ламп для замены. Проблема заключалась в большом разбросе времени наработки на отказ усилительных ламп, и хотя завод-изготовитель определял нормативный срок непрерывной работы, лампы почему-то отказывали, как попало. Естественно, возникало много вопросов. Например, почему разброс так велик и нерегулярен? И что можно сделать, чтобы ввести его в приемлемые рамки?

Этими вопросами и занялся У. Шухарт. С самого начала он был фанатиком применения статистических методов. Его коллега и друг Э. Деминг так писал об этом в статье, посвященной памяти У. Шухарта: «Управление качеством означало для него применение статистических методов всюду: от сырьевых материалов до готовых изделий и обратно - в разработке новых изделий, при пересмотре требований к сырью, в непрерывном цикле обработки результатов, получаемых при исследовании покупательского спроса и из других источников».

Хотя традиционный взгляд на контроль качества был обращен в то время на обнаружение и изъятие негодных изделий из партии продукции, У. Шухарт увидел возможность увеличения выхода годных изделий непосредственно в процессе производства. Профилактика, направленная на предотвращение брака или несоответствий, несомненно, важнее и полезнее, чем отбраковка, ибо отбраковка сама по себе не приводит к улучшению изделий: она лишь разделяет их на две группы - принимаемых и бракуемых. Качество как данной партии, так и будущих партий при отбраковке не меняется. В то же время профилактика, т. е. система мер, направленных на предотвращение появления некачественных изделий, ведет к улучшению будущих партий продукции.

В настоящее время для управления применяются различные статистические методы, однако этого множества основными принято считать так называемые «семь основных инструментов качества». К ним относят:

- контрольный листки;

- гистограммы;

- диаграммы Парето;

- причинно – следственные диаграммы (диаграммы Исикавы);

- диаграммы разброса;

- диаграммы стратификации (диаграммы расслоения статистических данных);

- контрольные карты.

Контрольный листок.

Контрольные листки – это форма для систематического сбора данных и автоматического их упорядочения с целью облегчения дальнейшего использования собранной информации. Он представляет собой бумажный бланк, на котором заранее напечатаны необходимые служебные данные и диапазоны контролируемых показателей, с тем чтобы можно было легко и точно записать данные измерений и упорядочить их для дальнейшего использования. Контрольные листки используются для получения ответа на вопрос «Как часто встречаются изучаемые события?». Типовая форма контрольного листка приведена на рисунке 1.

 

Контрольный листок №____

для сбора данных о пороках при производстве тентового материала

Наименование продукции материал с ПВХ покрытием для автотранспорта

Артикул ткани 3С – 81 – 96 – 03

Цех 7 Участок 2 Контролер Петрова Дата 26.11.09

Наименование порока	Номер партии П - 253	Общее количество пороков на погонный метр
Результат контроля (Количество пороков на метр погонный)
Концевые	////////////////////
Складки	///////////////
Засечки	////////
Вмятины	///
Грязь	//
Прочие дефекты	//
Итого

 

Контролер /Петрова/

Рис. 1. Возможная форма контрольного листка

В конце смены подводятся итоги и заполняется суммарный контрольный листок без указания контролеров, но с указанием фамилии подводящего итог, например, мастера участка.

Гистограмма.

Гистограмма - это инструмент, позволяющий зрительно оценить закон распределения величины разброса данных, а также принять решение о том, на чем следует сфокусировать внимание для целей улучшения процесса. Гистограмма отображается серией столбиков одинаковой ширины, но разной высоты. Ширина столбика представляет интервал в диапазоне наблюдений, высота - количество наблюдений (измерений), попавших в данный интервал. При нормальном законе распределения данных существует тенденция расположения большинства результатов наблюдений ближе к центру распределения (к центральному значению) с постепенным уменьшением при удалении от центра.

Гистограмма применяется главным образом для анализа значений измеренных параметров, но может использоваться и для оценки показателей возможностей процессов.

Систематизируя показатели качества и анализируя построенную для них гистограмму, можно легко понять вид распределения, а определив среднее значение показателя и стандартное отклонение, можно провести сравнение показателей качества с контрольными нормативами и таким образом получить информацию высокой точности.

Этапы построения гистограммы

1. Разработка формы контрольного листка для сбора первичных данных. Возможная форма контрольного листка приведена на рисунке 2.

 

2. Сбор статистических данных х_i, i = 1,2,..., N, характеризующих ход процесса, и заполнение второго столбца контрольного листка.

3. Определить диапазон данных (размах), вычитая наименьшее значение ряда из наибольшего.

4. Определить количество интервалов (карманов) n на гистограмме по формуле Стерджесса

n = 1 + 3,322lgN

 

 

Рекомендуемое число n лежит в пределах от 6 до 12 в зависимости от величины N.

Количество данных N	Число карманов n
23…45
46…90
91…180
181…360
361…723
724…1447
1448…2885

5. Определение размеров кармана осуществляется так, чтобы весь размах ряда, делился на интервалы равной ширины, т.е. h = R/n

 

 

Вычисление основных характеристик качества процесса по гистограмме

Построение гистограммы на практике производят для того, чтобы оценить качество выпускаемой продукции и качество процесса производства этой продукции. Наиболее часто для оценки качества процесса используют следующие характеристики:

Р_р — индекс пригодности процесса удовлетворять технический допуск (без учета положения среднего значения);

k — показатель настроенности процесса на целевое значение;

Р_pk ⁼ Р_p (1 -k) — оценка индекса пригодности процесса удовлетворять технический допуск с учетом положений среднего значения.

Ниже рассмотрены примеры вычисления перечисленных выше индексов (показателей) по параметрам построенной гистограммы.

На рис. 2 обозначены:

- среднее арифметическое значение результатов наблюдений х_i;

- размах результатов наблюдений R= 6σ = 0,035 мм, равный ширине основания гистограммы и в большинстве случаев близкий к шести значениям стандартных отклонений σ;

- нижняя граница поля допуска LSL = 9,975 мм;

- верхняя граница поля допуска USL = 10,025 мм;

- середина поля допуска (целевое значение)

Ц = (LSL + USD /2 = (10,025 + 9,975) / 2 = 10,000 мм;

- дополнительные (гипотетические) значения нижней (LSL)' и верхней (USL)' границ поля допуска, которые потребуются далее.

По имеющимся на рис. 2 данным могут быть вычислены следующие величины, характеризующие качество процесса производства валиков:

- оценка индекса пригодности процесса удовлетворять технический допуск (без учета положения среднего значения )

P_P = (USL - LSL)/6σ = (USL - LSL)/R = (10,025 – 9,975)/0,035 = 1,43

Если Р_P ≥ 1, то ширина гистограммы укладывается в пределах ширины поля допуска, т. е. процесс является управляемым; точнее говоря, имеется возможность осуществить процесс так, что 99,73 % изделий будут попадать в пределы поля допуска; если P _P < 1, то процесс является неуправляемым, так как размеры части изделий неизбежно будут выходить за пределы поля допуска. Большинство российских заводов работают при значениях Р_P ≈ 0,95... 1,3, а японским специалистам по управлению качеством продукции во многих случаях удается поддерживать на своих предприятиях значения индекса пригодности процессов Р_P ≈ 1,5... 4,0, что позволяет ограничить дефектность продукции единицами бракованных изделий на миллион выпускаемых изделий.

- смещение гистограммы относительно середины поля допуска может быть охарактеризовано показателем настроенности процесса на целевое значение

и для нашего примера k = 0,1.

Если среднее значение x_ср случайного распределения результатов наблюдений сместится относительно середины Ц поля допуска на величину половины поля допуска (USL — LSL) /2, то показатель настроенности процесса станет равен k = 1; если же х_ср = Ц, то показатель k = 0:

- наиболее полно качество протекания процесса может быть охарактеризовано величиной индекса пригодности процесса удовлетворять технический допуск с учетом положения среднего значения x_ср

P_Pk = P_P(1 - k)

который в рассматриваемом нами примере равен Р_рк = 1,43 (1 — 0,1) = 1,29.

Таким образом, для повышения качества процесса (уменьшения уровня дефектности) необходимо обеспечить высокое значение P_P и низкое значение k.

Диаграмма Парето.

Диаграмма Парето используется для:

- демонстрации распределения каждого пункта в общем воздействии по порядку важности;

- классификации возможностей улучшения по важности.

Диаграмма Парето представляет собой простое графическое представление пунктов по степени важности от наиболее частых до наименее частых. Диаграмма Парето основана на принципе Парето, который гласит, что часто лишь небольшое количество пунктов влияют на значительную часть воздействия. При разграничении наиболее важных и наименее важных пунктов наибольшее улучшение будет достигнуто при наименьшем усилии.

Анализ Парето - это способ организации данных, чтобы показать, из каких основных факторов состоит анализируемый объект. Это поиск смысла.

Диаграмма Парето - это тип графика, в котором строятся полосы в нисходящем порядке, начиная слева. Основой графика Парето является правило "80-20"; 80% проблем являются результатом 20% причин.

Чем полезен график Парето?

Расположение данных на графике Парето помогает выделить "жизненно важное меньшинство" по сравнению с "незначительным большинством". Выбор категорий, помещение данных в таблицу и построение графика Парето помогает улучшить общение между членами команды и с руководством. Это также позволяет команде выбрать компонент проблемы, который будет давать наибольшие результаты. Использование принципа Парето: позволяет выделить и реализовать в первую очередь те ресурсы, которые принесут максимальный доход.

Применение правила Парето для анализа качества продукции означает, что 80% всех дефектов вызывают 20% всех причин, их вызывающих. Отсюда следует, что 80% всех дефектов составляют только три вида отказов. Поэтому, следуя классическому анализу Парето, необходимо прежде всего искоренять причины именно этих видов дефектов.

Однако конечная цель повышения надежности не в уменьшении числа отказов, а в сокращении экономических потерь при эксплуатации объекта. На первый взгляд из данных о распределении отказов по видам дефектов следует, что целесообразно начинать с выявления причин отказов первой группы, так как число отказов по этой причине наибольшее. Но экономически выгоднее прежде всего устранить причины отказов, приносящих самые большие затраты на эксплуатацию объекта. Поэтому число данных по видам дефектов расширяется за счет информации по потерям и затратам.

Диаграмма Парето строится также как и обычная гистограмма, с той лишь разницей, что ставятся флажки в поле Парето (отсортированная диаграмма) и Интегральный процент.

Причинно – следственная диаграмма (диаграмма Исикавы).

Это очень практичный инструмент для анализа причин, приводящих к определенному результату. Причинно-следственная диаграмма используется для:

- анализа причинно-следственных связей;

- сообщения о причинно-следственных связях;

- облегчения решения проблемы от ее признака до причины.

Причинно-следственная диаграмма (ПСД) применяется для исследования и демонстрации связи между данным явлением (например, отклонениями характеристик качества) и его потенциальными причинами. Несколько потенциальных причин классифицируются по основным категориям и подкатегориям, так что их представление напоминает скелет рыбы. Отсюда и вытекает еще одно известное наименование этой диаграммы — диаграмма «рыбьи кости».

ПСД может быть построена индивидуально, но лучше это делать с помощью команды в режиме «мозгового штурма». При этом действуют все рекомендации по организации «мозгового штурма». К основным из них относятся: состав команды (в нее включают как узких специалистов разного профиля, так и людей далеких от данной проблемы, но с высоким творческим потенциалом), порядок работы, роль ведущего и др. Чаще всего ПСД строится для отдельной проблемы (результата) (рис. 3, 4). Если выявлено много факторов, ПСД может быть детализирована для отдельных (главных) факторов (причин). ПСД может быть построена и для ряда операций процесса (рис. 5).

 

Рис. 3. Причинно – следственная диаграмма с разделением причин по уровням.

Построение ПСД для проблемы. Детализация элементов ПСД.

1. Создается команда, уточняется формулировка проблемы. На большом листе справа посередине располагают название проблемы и рисуют стремящуюся к ней стрелку (см. рис. 3).

2. Команда генерирует идеи о главных причинах проблемы (в нашем случае «неудовлетворенность потребителей») и наносят их на ПСД (рис. 4). Здесь можно использовать принципы 5М для производства (персонал –manpower, технология – methods, материалы - materials, оборудование - machines, измерения - measurements) или 5Р для сферы услуг (персонал - personnel, процедуры - procedures, покупатели - patrons, окружающая среда - place, обеспечение - provisions).

Если речь идет о специфической проблеме, специалисты с производственным персоналом должны выявить главные причины появления данной проблемы.

Рис. 4. Причинно-следственная диаграмма для главных причин проблемы «потребители не удовлетворены»

Команда генерирует идеи о причинах первого уровня (непосредственно влияют на главную причину), второго уровня (непосредственно влияют на причину первого уровня) и т. д. для каждой главной причины. Эти причины могут наноситься на основную ПСД, как это показано на рисунке выше (см. рис. 3), или, если причин много и их формулировка сложна, для каждой главной причины может строиться своя ПСД. При высказывании идеи автор указывает, к какому уровню можно отнести данную причину. Этот вопрос обсуждается в команде.

Построение ПСД для процесса, состоящего из нескольких операций (этапов).

При коротких технологических цепочках возможно построение ПСД для каждой операции в этой цепи. При этом ставится задача улучшения не только отдельной операции (этапа), но и всего процесса в целом.

В этом случае можно выделить два основных этапа построения ПСД.

1. Идентифицируется ступенчатый процесс, и разрабатывается его блок-схема. Например, для общего процесса продаж могли бы быть идентифицированы следующие ступени: установление первоначального контакта с потребителем, разработка понимания потребностей потребителя, обеспечение потребителя информацией, предпродажные мероприятия и мероприятия по продаже.

2. Для каждой операции (этапа) выделяются главные и второстепенные факторы, способствующие повышению эффективности этой операции. Эти факторы наносят на изображение соответствующей операции на блок-схеме процесса (рис. 5). Здесь следует обратить внимание на стыковки этапов процесса. В реальной практике из-за бюрократических и других организационных проблем именно при переходе от одной операции к другой возникают различные проблемы, снижающие эффективность процесса. Такая ПСД позволяет выполнить более полный, комплексный анализ сложного многоэтапного процесса.

 

 

 

Рис. 5. Причинно-следственная диаграмма для многооперационного процесса (на примере процесса продаж)

Опыт применения ПСД позволяет сформулировать следующие рекомендации по их совершенствованию.

1. Каждую проблему следует рассматривать в максимально широком аспекте, учитывать как внутренние, так и внешние факторы. Если речь идет о социальных, экономических проблемах, необходимо принимать во внимание экономическую ситуацию в стране, на мировом рынке, налоговую политику государства, региональные особенности и т. п.

2. Каждое предложение о влияющих факторах или причинах изучаемой проблемы должно сразу наноситься на лист бумаги, где изображается ПСД, в определенное место. Это место предлагает автор идеи. Участники «мозгового штурма» могут высказывать по этому вопросу свое мнение. Решение принимается большинством голосов.

3. После окончания разработки ПСД все члены команды должны ее обдумать. Возможны консультации со специалистами — не членами команды. Через 1-3 дня целесообразно собраться и обсудить возникшие вопросы и предложения.

4. Полезно широкомасштабное обсуждение ПСД в коллективе организации, особенно если она посвящена решению важной для организации проблемы (например, расширению рынка, повышению качества продукции и т. п.). Для этого можно вывесить ПСД в крупном масштабе на доске объявлений, раздать работникам ее копии или сбросить информацию на их компьютеры. Через примерно две недели следует собрать предложения и обсудить их в команде по разработке ПСД с участием авторов.

5. В команду по разработке ПСД следует включить непосредственных исполнителей работ, которые предполагается совершенствовать. Это могут быть и операторы оборудования, и наладчики, и контролеры, и бухгалтеры, и др. Эти люди знают проблемы изнутри и могут предложить эффективные меры по их решению.

Очень часто при построении диаграммы Парето сначала проводят причинно – следственный анализ (строят ПСД), а уже потом строят собственно диаграмму Парето.

Диаграммы стратификации (диаграммы расслоения статистических данных).

Стратификация – разделение полученных данных на отдельные группы (слои, страты) в зависимости от выбранного стратифицирующего фактора.

В качестве стратифицирующего фактора могут быть выбраны любые параметры, определяющие особенности условий возникновения и получения данных:

- различное оборудование;

- операторы, производственные бригады, участки, цехи, предприятия и т. п.;

- время сбора данных;

- разные виды сырья;

- различие используемых станков, средств измерения и т. д.

При отсутствии учета стратифицирующего фактора (расслоения данных) происходит их объединение и обезличивание, затрудняющее установление действительной взаимосвязи между полученными данными и особенностями их возникновения.

Например, при анализе источника дефектной продукции, поставляемой предприятию несколькими сторонними поставщиками, целесообразно в качестве стратифицирующего фактора выбрать поставщиков и произвести стратификацию дефектной продукции по поставщикам.

Специалисты по управлению качеством продукции очень часто при стратификации используют метод 4M…5M. Наиболее часто производится группировка статистических данных по первым четырем причинам (метод 4М).

Применение метода стратификации основано на том, большинство случайных процессов в экономике, технике, медицине и пр., распределены по нормальному закону. Отсюда следует, что если на построенной гистограмме процесса в целом на ней выделяется несколько пиков (мод, максимальных значений), то можно предположить, что эта гистограмма является простой суммой нескольких одномодовых гистограмм с разным значением мод, а каждая из этих гистограмм соответствует какому – либо стратифицируемому фактору. После разделения можно строить диаграммы Исикавы или Парето.

При практическом использовании метода стратификации рекомендуется действовать следующим образом:

1. Выберите данные, представляющие интерес для изучения;

2. Выберите стратифицирующий фактор и категории группы, на которые будут разделяться данные;

3. Произведите группировку данных на основании выбранных категорий;

4. Оцените результаты группировки по каждой из категорий;

5. Соответствующим образом представьте полученные результаты;

6. Проанализируйте необходимость дополнительного изучения данных;

7. Спланируйте последующую работу для дополнительного подтверждения полученных результатов.

Рассмотрим применение метода стратификации на примере анализа качества изделий в одном из цехов предприятия. Пусть после сбора статистических данных была построена гистограмма, отображающая случайное распределение главного параметра х качества продукции, представленная на рис. 6а. Из этого рисунка видно, что распределение близко к равномерному, размах R_ц статистических данных для этого цеха занимает почти все поле допуска, индекс пригодности процесса Р_P ≈ 1,09 (не намного больше единицы).

В процессе стратификации осуществим группировку (расслоение) статистических данных по трем сменам, работающим в цехе. Результаты такой работы представлены на рис. 6 б, в, г. Видно, что распределение статистических данных в каждой из трех смен близко к нормальному, причем размахи R₁, R₂, R₃ (ширина основания гистограмм для каждой смены) относительно невелики, а средние арифметические значения х₁, x₂, x₃ главного параметра качества продукции в каждой смене сильно отличаются друг от друга.

 

 

Рис. 6.Стратификация статистических данных о качестве продукции цеха по трем сменам

а – гистограмма для всего цеха;

б,в,г – гистогаммы соответственно для 1 – й, 2 – й и 3 – й смен;

д – гистограмма распределения главного параметра качества продукции цеха после совмещения средних значений 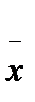₁, ₂, ₃ для каждой смены с серединой Ц поля допуска.

По результатам стратификации статистических данных (см. рис. 6 6, в, г) могут быть сформулированы следующие предложения по улучшению качества продукции цеха. Например, качество продукции может быть повышено за счет проведения только организационно-технических мероприятий без капитальных вложений в новые более точные станки и оборудование, а именно после разработки и внедрения мероприятий, направленных на то, чтобы средние арифметические значения x₁, x₂, x₃ в каждой смене максимально приблизились к значению середины Ц поля допуска.

После выполнения этих мероприятий суммарная гистограмма для цеха в целом примет вид, показанный на рис. 6д.

Из рис. 6д видно, что при совмещении средних арифметических значений главного параметра качества x₁, x₂, x₃ для каждой смены с серединой Ц поля допуска суммарная гистограмма для цеха в целом имеет значительно меньший размах R_ц' < R_ц, что соответствует значению индекса пригодности процесса Р_P ≈ 2,56.

Диаграммы разброса.

На практике часто важно изучить зависимости между парами каких-либо переменных. Как можно, например, установить, зависит ли вариация размеров детали от изменений скорости вращения шпинделя токарного станка? Или, допустим, мы хотим управлять концентрацией материала, но предпочитаем заменить измерение концентрации измерением плотности, поскольку на практике ее гораздо легче измерить. Для изучения зависимостей между двумя переменными, такими как скорость вращения шпинделя токарного станка и размер детали (или концентрация и плотность), мы можем воспользоваться так называемой диаграммой рассеивания.

Диаграмма разброса (рассеивания) — инструмент, позволяющий определить вид и тесноту связи между парами соответствующих переменных.

Эти две переменные x и у могут относиться:

а) к характеристике качества и к влияющему на нее фактору х;

б) к двум различным характеристикам качества х и у;

в) к двум факторам х и у, влияющим на одну характеристику качества z.

Для выявления связи между ними и служит диаграмма разброса (рассеивания), которую также часто называют полем корреляции. При выяснении тесноты связи между парами переменных важно прежде всего построить диаграмму рассеивания и понять ситуацию в целом.

Этапы построения диаграммы разброса (рассеивания)

Можно рекомендовать различные способы построения диаграммы разброса (рассеивания), один из них таков.

1. Соберите парные данные (х, у), между которыми вы хотите исследовать зависимость, и расположите их в таблице (табл. 1). При построении таблицы необходимо иметь по меньшей мере 30 пар данных.

Таблица 1

Данные для построения диаграммы разброса

x	x1	x2	…	xn
y	y1	y2	…	yn

 

2. Найдите максимальные и минимальные значения для х и у. Выберите шкалы на горизонтальной и вертикальной осях так, чтобы обе длины рабочих частей осей х и у получились приблизительно одинаковыми (чтобы они уместились на экране компьютера или на стандартном листе бумаги), тогда диаграмму будет легче читать. При определении масштабов возьмите на каждой оси от 3 до 10 градационных делений и при обозначении этих делений используйте (для облегчения чтения) круглые числа. Если одна переменная — фактор, а вторая — характеристика качества, то выберите для фактора горизонтальную ось х, а для характеристики качества — вертикальную ось у.

3. На экране компьютера (на отдельном листе бумаги) начертите график и нанесите на него данные. Если в разных наблюдениях получаются одинаковые значения, покажите эти точки, либо рисуя концентрические кружки, либо нанося вторую точку рядом с первой.

4. Нанесите на диаграмму все необходимые обозначения, например:

а) название диаграммы;

б) интервал времени сбора данных;

в) число пар данных;

г) названия и единицы измерения для каждой оси;

д) дата составления диаграммы;

е) имя (и прочие данные) человека, который составлял эту диаграмму.

Убедитесь, что перечисленные выше данные, отраженные на диаграмме, понятны любому человеку, а не только тому, кто строил диаграмму.

После построения диаграммы рассеивания необходимо изучить связи между х и у, но для установления силы связи в количественных терминах полезно вычислить коэффициент корреляции, который принимает значение из диапазона -1 ≤ r ≤ 1. Если абсолютное значение rокажется больше 1, то совершенно ясно, что произошла ошибка и вы должны пересчитать результат.

Задание.

Группу разделить на подгруппы по 2 – 3 человека.

Загрузить электронные таблицы Excel и проверить наличие команды Анализ данных в меню Сервис. При ее отсутствии выбрать в этом же меню команду Надстройки и поставить флажок у надстройки «Пакет анализа ».

В пакет анализа данных включены основные инструменты статистического анализа (окно Анализ данных).

Для моделирования данных используется инструмент Генерация случайных чисел, позволяющий моделировать данные с различными распределениями: нормальным, равномерным, биномиальным и другими.

Смоделируйте три столбца по 500 нормально распределенных чисел со средним значением 10, 25 и 40 соответственно и стандартным отклонением 2. Для этого в окне Генерация случайных чисел в поле Распределение выбрать Нормальное, в поле Число переменных ввести число 1, в поле Число случайных чисел ввести число 500, в поле Среднее – 10, в поле Стандартное отклонение – 2. В поле Выходной интервал ввести выделенную ячейку А1. Нажать кнопку ОК. Разрядность получившегося ряда уменьшить до 2 – х знаков после запятой (в дальнейшем все действия производить с этой разрядностью). Аналогично сформировать два оставшихся столбца, введя средние значения 25 и 40 соответственно, а в качестве выходных ячеек выбрав В1 и С1.

Поле Случайное рассеивание используется для фиксации определенной совокупности случайных чисел: если оно не заполнено, каждый раз будет моделироваться разный набор случайных чисел. Если же в этом поле стоит какое-то число, то этому числу будет соответствовать вполне определенная последовательность случайных чисел.

Рассматривая смоделированные данные как генеральную совокупность, сделайте из них три случайные выборки (по одной из каждого столбца) по 70 чисел.

Алгоритм действий:

1. Анализ данных → Выборка → ОК.

2. Входной интервал → А1:А500.

3. Метод выборки → Случайный → Число выборок – 70.

4. Выходной интервал → Е1.

ОК.

Аналогичные операции проделать для столбцов В и С. Данные поместить в столбцы F и G.

Определение характеристик выборки

Для определения числовых характеристик выборки можно воспользоваться статистическими функциями, однако большинство характеристик можно получить проще, используя инструмент Описательная статистика того же пакета анализа.

Алгоритм действий:

1. Анализ данных → Описательная статистика→ ОК.

2. Входной интервал → Е1:70.