УСТОЙЧИВОСТЬ СФЕРИЧЕСКИХ СЕГМЕНТОВ.

УСТОЙЧИВОСТЬ СФЕРИЧЕСКИХ И ЭЛЛИПСОИДАЛЬНЫХ ОБОЛОЧЕК

УРАВНЕНИЯ МЕСТНОЙ ПОТЕРИ УСТОЙЧИВОСТИ

СФЕРИЧЕСКИХ ОБОЛОЧЕК В РАЗНОСТНОЙ ФОРМЕ.

УСТОЙЧИВОСТЬ СФЕРИЧЕСКИХ СЕГМЕНТОВ.

Будем исходить из общих уравнений В. З. Власова, которые для случая сферы, находящейся под равномерным внешним дав­лением, принимают вид ( ),

(1.1)

где

Вначале рассмотрим осесимметричные формы потери устой­чивости сферических сегментов. Представляя оператор Ла­пласа в виде

получим следующую запись системы (12.1):

(1.2)

Для изгибающих моментов и мембранных усилий имеем выражения

В случае осесимметричной формы потери устойчивости сфе­рической оболочки эти выражения принимают вид

~

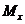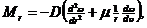
~ (1.3)

~ ~

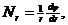
Запишем уравнения (1.2) — (1.3) в конечных разностях:

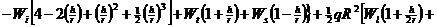(1.4)

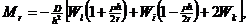
Здесь — шаг сетки.

Для того чтобы написать исходные уравнения (1.2) в ко­нечных разностях в точке г = 0, необходимо сначала найти пре­делы некоторых дифференциальных выражений при г=0. При­меняя правило Лопиталя, получим

Тогда исходные уравнения (1.2) для точки = 0 примут вид

или в конечных разностях

(1.5)

Используем уравнения (1.4) и (1.5) для определения кри­тического внешнего давления сферических сегментов. Вначале

Рис. 1.

 

рассмотрим случай шарнирного опирания сегмента. Граничные условия для этого случая будут

Дополнительные радиальные мембранные напряжения на контуре сегмента примем . В развернутом виде эти гранич­ные условия при шаге сетки (рис. 1) примут вид

откуда

На контуре сегмента функция напряжений будет равна кулю. Это вытекает из связи функции напряжений с изгибающим моментом от нагрузки, действующей на контуре [4]. В нашем случае контурная нагрузка . Следовательно,

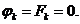
Уравнения равновесия для точки будут иметь вид

Из этих уравнений найдем

Рассматривая в этом выражении шаг сетки h как параметр, найдем

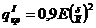при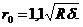

Теперь рассмотрим сетку с двумя точками (рис. 192)

Рис. 2.

 

В этом случае для законтурной точки имеем уравнение

откуда

Точка 1:

Точка 2:

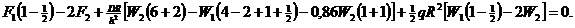
Исключая из этих уравнений и ,получим

где

Из условия равенства нулю определителя этих уравнений получим

где

 

В табл. 12 даны значения в зависимости от параметра k.

Таблица 12

 

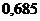
Из этой таблицы найдем

при и

Более точное значение критического давления можно опре­делить экстраполяцией:

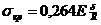при

При решении этой же задачи для случая жесткой заделки контура (рис. 3) и при тех же граничных условиях дляфункции напряжений в результате первого и второго приближений и экстраполяции получим следующее значение критического давления:

при

Теперь рассмотрим устойчивость сферического сегмента с жестким недеформируемы контуром при внешнем давлении. В этом случае, кроме требова­ния равенства нулю угла поворота, необходимо поставить дополнитель­ное требование об отсутствии удли­нения окружности опорного контура, т. е.

 

Рис. 3.

В конечных разностях эти условия имеют вид

В рассматриваемой задаче ввиду недеформируемости опор­ного контура после потери устойчивости возникнут дополнитель­ные мембранные напряжения . Если осевую линию контура сегмента рассматривать как кольцо, нагруженное равномерной нагрузкой где — толщина сегмента, то изгибающий момент в этом кольце от такой нагрузки будет равен нулю. Учи­тывая указанную выше связь изгибающего момента с функцией напряжений, можно показать, что эта функция на контуре будет . Тогда

Первое приближение: (рис. 4):

Из этих уравнений получим

Минимум этого выражения по параметру

при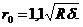

Рис. 4.

 

В результате второго приближения 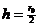(рис. 5) было получено

где

 

Рис. 5.

 

В табл. 13 приведена зависимость от параметра .

Таблица 13

 

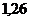
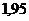
Из этой таблицы найдем

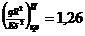при

 

Более точное значение критического давления можно опре­делить экстраполяцией:

при