Решение всех задач (обнаружение, распознавание-различение, измерение параметров сигнала) всегда затрудняется наличием помех искусственного или естественного происхождения. С точки зрения характера воздействия помех на работу систем и принципов их защиты помехи целесообразно разделить на группы: шумы, мешающие излучения и мешающие отражения. Как и сигналы, помехи являются электромагнитными полями и характеризуются пространственной, поляризационной и временной структурой. Однако, как и в случае с сигналами сосредоточим внимание только на их временной структуре.
Внутренние шумы приемных устройств, а также внешние активные шумовые помехи, преднамеренно создаваемые для противодействия работе РТС, имеют подобные временные структуры и поэтому рассматриваются объединение.
Шум (мешающие излучения) представляет собой нормальный случайный процесс с флуктуирующей амплитудой и фазой:
h(t) = H(t) exp(iω0t) = xh(t) + iyh(t),
где H(t) - комплексная огибающая шума
xh(t), yh(t) - квадратурные составляющие шума.
Одна из квадратурных составляющих шума показана на рис.1 Корреляционная функция шума является результатом статистического усреднения

где σш2 - средняя мощность шума,
rш(τ) - нормированная корреляционная функция шума.
Заметим, что средние значения шума, его комплексной огибавшей и квадратурных составляющих равны нулю:


Рис.1. Одна из квадратурных составляющих шума.

Рис.2. Нормированная корреляционная функция шума.

Рис.3. Энергетический спектр шума.
Нормированная корреляционная функция шума чаще всего аппроксимируется экспонентой (рис.2):
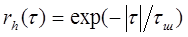
где τш - время корреляции шума.
Энергетический спектр шума
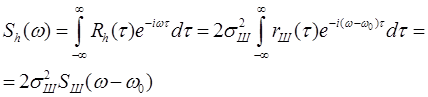
есть смещенный по частоте на величину несущий ω0 энергетический спектр флуктуации шума:

При экспоненциальной корреляционной функции шума энергетический спектр флуктуации шума имеет форму резонансной кривой одиночного колебательного контура (рис.3):
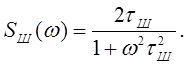
Ширина спектра шума обратно пропорциональна удвоенному времени корреляции:
∆fш = 1/2τш
Отношение средней мощности шума к ширине спектра называется спектральной плотностью шума:
N0 = σш2/∆fш
Практически ширина спектра шума всегда превосходит ширину спектра сигнала и полосу пропускания устройств обработки сигнала ∆fш >> ∆f0. Это означает, что в интересующем нас диапазоне частот можно пренебречь некоторым изменением энергетического спектра шума, считая его равномерным:
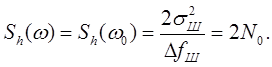
Равномерный энергетический спектр является полезной математической идеализацией спектров. Случайный процесс с равномерным спектром называют белым шумом по аналогии с белым светом, имеющим сплошной и приблизительно равномерный спектр в пределах видимой его части (рис.4).
Корреляционная функция белого шума, являясь обратным преобразованием Фурье энергетического спектра, равна
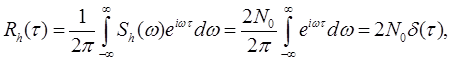
т.е. представляет собой дельта-функцию, а нормированная корреляционная функция для белого шума (рис.5):

Таким образом, белый шум характеризуется тем, что его значения в любые два сколь угодно близких момента времени не коррелированы.
Вероятностные характеристики шума описываются многомерной плотностью вероятности совокупности его дискретных значений, взятых с интервалом времени ∆t >> τш. При этом корреляционные свойства его дискретных значений описываются символом Кронекера δkl:
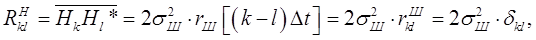
где

При этом определитель корреляционной матрицы шума и элементы обратной корреляционной матрицы шума описываются следующими выражениями:
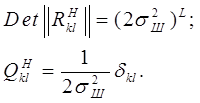
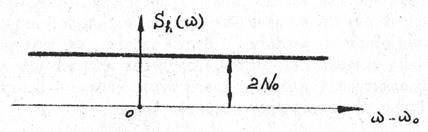
Рис.4. Энергетический спектр белого шума.
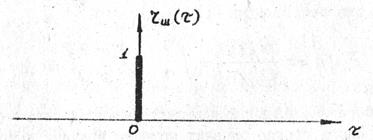
Рис.5. Нормированная корреляционная функция белого шума.
где L - число дискретных значений шума на некотором интервале наблюдения.
Многомерная плотность вероятности шума оказывается произведением соответствующих плотностей вероятности для различных дискретных значений шума:

что оказывается следствием независимости дискретных значений шума. Одномерные распределения квадратурных составляющих, амплитуды, фазы и мгновенной мощности шума аналогичны соответствующим распределениям для принятого сигнала.
Мешающие отражения являются результатом наложения нерегулярно возникающих элементарных сигналов стандартной формы со случайной фазой и амплитудой, и поэтому представляют собой случайный процесс с нормальным (гауссовым) распределением вероятности мгновенных значений. Если при отражении сигнала от объекта с малыми размерами можно пренебречь "размыванием" закона модуляции, то при отражении от протяженного - говорить о форме сигнала, похожей на форму зондирующего сигнала нельзя.
Задача обнаружения и методика ее решения.