1. Разработать математическую модель задачи, т.е. записать математические выражения для функции цели и ограничений на переменные.
2. Выполнить проектирование табл. 8, т.е. ввести в рабочий лист исходные данные согласно образцу:
Таблица 8
| А | В | С | D | E | F | G | Н | ||
| Задача о планировании производства | |||||||||
| Переменные и исходные данные | |||||||||
| Имя | Х1 | Х2 | Х3 | Х4 | ЦФ | Направ. | |||
| Значение | Max | ||||||||
| Прибыль | |||||||||
| Виды продукции | Ограничения | ||||||||
| Ресурсы | А1 | А2 | А3 | А4 | Левая часть | Знак | Правая часть | ||
| Р1 | <= | ||||||||
| Р2 | <= | ||||||||
| Р3 | <= | ||||||||
| Р4 | <= | ||||||||
| Р5 | <= | ||||||||
| Х1: Х4 | >= | ||||||||
В ячейки В4:Е4 вводятся начальные значения управляемых переменных, в данном случае – это нули.
3. В ячейке G4 необходимо записать в виде формулы выражение для целевой функции как результат вычисления с использованием функции СУММПРОИЗВ(B4:E4;B5:E5) c помощью Мастера функций.
4. В ячейке F8с помощьюэтой же функции записывается левая часть ограничения для ресурса Р1 в виде формулы СУММПРОИЗВ($B$4:$E$4;B8:E8). Затем эта формула копируется в ячейки с F9поF12.
5. Для решения задачи оптимизации воспользуемся командой Данные, Поиск решения, предварительно установив курсор в ячейку G4, предназначенную для целевой функции. Появляется диалоговое окно Поиск решения, в котором надо установить значения в следующие окна ввода:
1) Установить целевую ячейку – щелкнуть по ячейке G4(если курсор предварительно уже был установлен на этой ячейке, адрес G4здесь появляется автоматически);
2) Равной Максимальному значению – нажать соответствующую кнопку;
3) Изменяя ячейки – протащить мышь по ячейкам В4:Е4, предназначенным для хранения результата вычислений, т.е. неизвестных значений переменных Х1: Х4;
4) Ограничения – нажать кнопку Добавить и в появившемся диалоговом окне ввести:
- в левое поле ввода – адреса ячеекF8:F12, соответствующих ранее сформированным выражениям, стоящим в левых частях ограничений по ресурсам;
- в среднее поле ввода – соответствующий знак ограничения;
- в правое поле ввода - адреса ячеекН8:Н12,соответствующих значениям ресурсов Р1:Р5.
- нажать кнопку Добавить, ввести условия неотрицательности независимых переменных х1:х4,используя адреса ячеек В4:Е4,отведенных для записи вычисляемых значенийх1:х4,и ячейку Н13, в которую ранее было введено число 0. Нажать кнопку ОК.
6. Нажать кнопку Параметры, появится новое диалоговое окно Параметры поиска решения. Здесь надо установить флажок Линейная модель,что обеспечивает применение симплекс-метода. При решении большинства задач значения остальных параметров можно использовать по умолчанию. Нажать кнопку ОК.
7. Снова появится окно Поиск решения, здесь нажать кнопку Выполнить. Появится диалоговое окно Результаты поиска решения и активизировать названия отчетов Результаты, Устойчивость, Пределы. Нажать кнопку ОК.
8. Выполнить анализ оптимального решения с использованием отчетов Результаты, Устойчивость и Пределы.
Отчет по результатам состоит из трех таблиц Excel.
Ø Таблица «Целевая ячейка» содержит значение целевой функции. В столбце Исходно приведено значение целевой функции до начала вычислений.
Ø Таблица «Изменяемые значения» приводит значения искомых переменных, полученные в результате решения задачи.
Ø Таблица «Ограничения» показывает результаты оптимального решения для ограничений и для граничных условий. Для Ограничений в графе Формула приведены зависимости, которые были введены в диалоговое окно Поиск решения; в графе Значение приведены величины использованного ресурса; в графе Разница показано количество неиспользованного ресурса. Если ресурс используется полностью, то в графе Состояние указывается связанное;при неполном использовании ресурса в этой графе указывается не связан.
Для Граничных условий приводятся аналогичные величины с той лишь разницей, что вместо величины неиспользованного ресурса показана разность между значением переменной в найденном оптимальном решении и заданным для нее граничным условием.
Отчет по устойчивости состоит из двух таблиц.
Ø Таблица «Изменяемые ячейки» содержит следующие значения для переменных:
- в столбце Результ. Значение – результат решения задачи, т.е. значения переменных, придающих целевой функции экстремальное значение;
- в столбце Редуц. (Нормир.) Стоимость редуцированная стоимость показывает, на сколько единиц изменится целевая функция при принудительном выпуске одной единицы данного вида продукции; повторить решение, добавив ограничение х1>=1;
- столбец Целевой Коэффициент – значения коэффициентов целевой функции;
- столбец Допустимое увеличение показывает, насколько можно увеличить коэффициент целевой функции без изменения структуры оптимального решения;
- столбец Допустимое уменьшение показывает, насколько можно уменьшить коэффициент целевой функции без изменения структуры оптимального решения.
Ø Таблица «Ограничения» содержит данные по ограничениям:
- столбец Результ. Значение – количество использованных ресурсов;
- столбец Теневая цена – двойственную оценку, т.е. величину изменения целевой функции при изменении величины ресурса на единицу; при этом, если теневая цена имеет положительный знак, то целевая функция возрастает при увеличении ресурса, если цена отрицательна – то целевая функция убывает при увеличении ресурса;
- в столбце Ограничение Правая часть – исходные данные по ресурсам;
- столбец Допустимое увеличение показывает, на какую величину можно увеличить запас ресурса, при котором происходит увеличение целевой функции и сохраняется оптимальный набор переменных, входящих в оптимальное решение;
- столбец Допустимое уменьшение - показывает, на какую величину можно снизить запас ресурса, при котором сохраняется полученное оптимальное значение целевой функции.
Отчет по пределам показывает, в каких пределах можно изменять выпуск продукции при сохранении структуры оптимального решения:
- столбец Значение - содержит оптимальные значения переменных;
- столбцы Нижний (Верхний) предел и Целевой результат показывают нижние (верхние) предельные значения объемов выпускаемой продукции и соответствующие значения целевой функции.
9. Исследовать влияние на оптимальное решение теневой цены для ресурсов Р1, Р2 , Р3.
Задача 2. Химическое предприятие может выпускать продукцию по трем технологическим способам. При этом за 1 ч по первому способу оно выпускает 20 ед., по второму – 25 ед., по третьему – 30 ед. продукции. Объём ресурсов, расходуемых за 1 ч, и количество имеющихся ресурсов представлены в таблице:
Таблица 9
| Факторы | ||||||
| Способ производства | Сырьё | Станочный парк | Рабочая сила | Энергия | Транс-порт | Прочие расходы |
| Ресурсы |
Спланировать работу предприятия из условия получения максимума продукции, если известно, что общее время работы предприятия составляет не более 30 ч.
6. Решение распределительной задачи
Задачи планирования распределения ресурсов (используются и для текущего и для перспективного планирования).
а) Параметры и размерность задачи:
| Наименование параметра | Обозначение в модели |
| Количество видов готовой продукции (количество технологических способов производства) | n |
| Количество видов используемых ресурсов (производственных факторов) | m |
| Нормы затрат ресурсов (факторов) (в расчете на 1 ед. продукции) | аij, 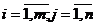
|
| Цены на готовую продукцию, предполагаемая прибыль (в расчете на 1 ед. продукции), удельные затраты на производство готовой продукции | cij, 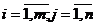
|
| Лимиты производственных ресурсов (факторов) | bi, 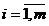
|
| Установленные нормативы по выполнению планового выпуска продукции | bj, 
|
б) Управляемые переменные X = (x11,x12,…,xij,..,xmn) – планируемые объемы выпуска продукции каждого вида.
в) Формализация ограничений: основные ограничения должны гарантировать, с одной стороны, что общий расход потребляемых ресурсов (производственных факторов) не должен превышать запасы этих ресурсов:
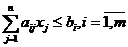 ,
,
а с другой – обеспечить плановый выпуск готовой продукции:
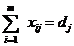 ,
,  .
.
Дополнительные ограничения связаны с неотрицательностью управляемых переменных.
г) Критерии эффективности:
- максимизация стоимости выпуска:
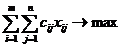 , где cij – цена единицы готовой продукции;
, где cij – цена единицы готовой продукции;
- минимизация трудоемкости производства продукции (расхода ресурсов):
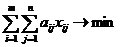 , где аij – расходы ресурсов или время, затраченное на производство единицы готовой продукции по каждому производственному фактору;
, где аij – расходы ресурсов или время, затраченное на производство единицы готовой продукции по каждому производственному фактору;
- минимизация затрат на производство готовой продукции:
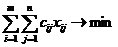 , где cij – затраты (себестоимость)на производство единицы готовой продукции;
, где cij – затраты (себестоимость)на производство единицы готовой продукции;
- максимизация прибыли от реализации выпуска:
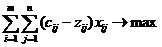 , где cij – цена единицы готовой продукции, zij – затраты на производство единицы продукции.
, где cij – цена единицы готовой продукции, zij – затраты на производство единицы продукции.
Задача. Четыре различных вида изделий (А, В, С, Д) могут изготовляться из трех видов взаимозаменяемого сырья (I, II, III). В связи с различными отпускными ценами на 1 ед. изделия в зависимости от используемого сырья и различными производственными затратами при использовании различного сырья, прибыль, получаемая от реализации 1 ед. изделия, зависит от вида продукции и используемого при его изготовлении вида сырья. В табл. 19 приведены исходные данные задачи: Таблица 19
| Сырье | Нормы расхода, кг/шт. | Прибыль, руб./шт | Запасы сырья, кг | ||||||
| А | В | С | Д | А | В | С | Д | ||
| I II III | 4,5 | ||||||||
| Плановое задание, шт. | - |
Составить оптимальный план, максимизирующий прибыль.