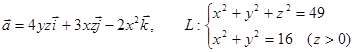ВЫСШАЯ МАТЕМАТИКА
ИРЭ (ЭР–1,2,4,5,6)+Эл-15
2 семестр, 12+11, 2011/2012 уч. год
ЭКЗАМЕНАЦИОННАЯ ПРОГРАММА
1.Функции нескольких переменных. Предел, непрерывность. Линии уровня и поверхности уровня. Частные производные функции нескольких переменных и их геометрический смысл в случае функции двух переменных.
2. Дифференцируемость функции двух переменных. Необходимое условие дифференцируемости функции в точке. Полный дифференциал. Достаточные условия дифференцируемости (без доказательства). Частные производные и дифференциалы высших порядков. Теорема о равенстве смешанных производных (без доказательства).
3. Дифференцирование сложной функции. Инвариантность формы первого дифференциала. Понятие неявной функции. Теорема существования и дифференцируемости неявной функции (без доказательства). Вычисление производных неявной функции.
4. Скалярное поле. Примеры. Градиент скалярного поля, производная по направлению и ее связь с градиентом. Свойства градиента скалярного поля. Инвариантное определение градиента.
5. Касательная плоскость и нормаль к поверхности. Формула Тейлора для функции нескольких переменных. Локальный экстремум функции нескольких переменных. Необходимое условие экстремума. Достаточное условие экстремума функции двух переменных.
6. Наибольшее и наименьшее значение непрерывной функции нескольких переменных на замкнутом ограниченном множестве. Условный экстремум. Метод множителей Лагранжа.
7. Кратные (двойные и тройные) интегралы. Определение, теоремы существования, свойства. Теорема Фубини (сведение к повторным интегралам (без док-ва)). Перемена порядка интегрирования. Вычисление площадей, объемов, некоторые приложения кратных интегралов.
|
|
8. Замена переменных в кратных (двойных и тройных) интегралах (без док-ва). Якобиан и его геометрический смысл. Двойной интеграл в полярных координатах. Тройной интеграл в цилиндрических и сферических координатах.
9. Площадь поверхности и её вычисление. Поверхностный интеграл первого рода,
его свойства и вычисление.
10.Векторное поле, векторные линии. Векторные трубки. Примеры. Поток
векторного поля через поверхность, его физический смысл. Свойства потока
векторного поля, вычисление потока.
11.Формула Остроградского-Гаусса. Дивергенция векторного поля, ее физический
смысл, свойства и инвариантное определение.
12.Криволинейный интеграл второго порядка. Свойства и вычисление. Формула
Грина. Циркуляция. Формула Стокса. Ротор векторного поля, его физический
смысл и свойства.
13.Соленоидальное поле. Примеры. Условия соленоидальности. Потенциальное
поле, условия потенциальности. Примеры. Условия независимости
криволинейного интеграла второго рода от формы пути интегрирования.
Интеграл в потенциальном поле.
14.Числовая последовательность. Предел числовой последовательности, его
свойства. Арифметические действия с последовательностями, имеющими
предел. Ограниченность последовательности, имеющий предел. Существование
предела у ограниченной монотонной последовательности.
15.Числовые ряды. Сумма и сходимость ряда. Остаточный член. Арифметические
операции с рядами. Необходимый признак сходимости. Ряды с положительными
членами. Признаки сравнения.
|
|
16.Достаточные признаки сходимости рядов. Даламбера, Коши; интегральный
признак Коши.
17.Знакопеременные и знакочередующиеся ряды. Абсолютная и условная
сходимость. Теорема Лейбница. Оценка сходящегося ряда. Арифметические
действия с абсолютно сходящимися рядами.
18.Функциональный ряд. Поточечная и равномерная сходимость. Область
сходимости. Признак Вейерштрасса.
19.Свойства равномерно сходящихся рядов: непрерывность суммы, интегрирование
и дифференцирование функциональных рядов. Степенные ряды. Теорема Абеля.
Интеграл сходимости. Непрерывность суммы степенного ряда.
20.Интегрирование и дифференцирование степенного ряда (без док-ва). Ряд
Тейлора. Разложение функции в ряд Тейлора. Необходимое и достаточное
условие разложения в ряд Тейлора. Достаточные условия разложения в ряд
Тейлора.
21.Единственность разложения в ряд Тейлора. Разложение основных элементарных
функций в ряд Тейлора. Применение степенных рядов.
22.Тригонометрическая система функций. Тригонометрический ряд Фурье, условия
его сходимости и свойства суммы.
23.Тригонометрические ряды Фурье для четных и нечетных функций, их свойства.
Ряды Фурье по косинусам и синусам, условия их сходимости и свойства суммы.
ЭКЗАМЕНАЦИОННЫЕ ЗАДАЧИ (образцы)
1. Исследовать на сходимость ряд
, 
, 
, 
.
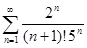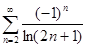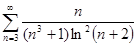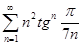2. Найти область сходимости ряда
, 
.
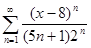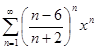3. Вычислить с точностью 0,001: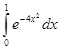 
.
4. Вычислить сумму ряда с точностью 0,1: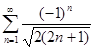 
5. Разложить функцию 
в ряд Фурье по синусам и по косинусам на интервале 
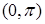и построить график суммы ряда 
.
.
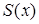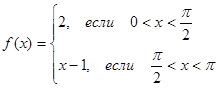6. Разложить функцию в ряд Фурье на интервале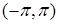 
и построить график суммы ряда .
|
|
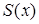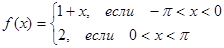
7. Разложить в ряд Тейлора по степеням x: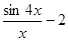 
, 
.
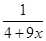8. Изменить порядок интегрирования:
, 
.
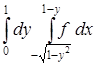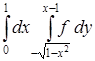9. Найти объем тела, заданного ограничивающими его поверхностями:
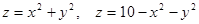
10. Найти объем тела, заданного ограничивающими его поверхностями:
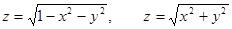
11. Найти площадь фигуры, ограниченной данными линиями:
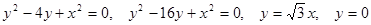
12. Найти площадь фигуры, ограниченной данными линиями:
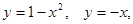
13. Найти поток векторного поля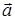 
через замкнутую поверхность S
(нормаль внешняя).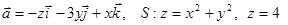 
14. Найти поток векторного поля 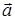через замкнутую поверхность S
(нормаль внешняя).
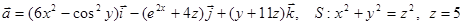
15. Найти циркуляцию векторного поля 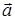вдоль контура L
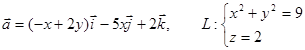
16. Найти циркуляцию векторного поля 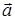вдоль контура L
