ЗАДАНИЕ 2
Формализм углового момента
1. Для частицы со спином ½ найти собственные значения и собственные функции операторов  ,
,  и
и  соответственно.
соответственно.
2. Определите вид матриц операторов 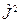 ,
, 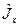 ,
,  ,
,  ,
,  ,
,  для случая
для случая  в представлении собственных функций оператора
в представлении собственных функций оператора  . Определите собственные векторы и собственные значения матриц
. Определите собственные векторы и собственные значения матриц 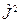 ,
, 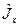 ,
,  ,
,  .
.
3. Определите среднее значение проекции момента на направление единичного вектора 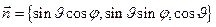 в состоянии
в состоянии 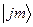 , где
, где 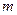 есть проекция момента на ось
есть проекция момента на ось 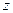 .
.
4. Найти средние значения величин  ,
,  ,
,  в состояниях
в состояниях 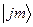 , где а)
, где а)  ,
,  ; б)
; б)  ,
,  ; в)
; в)  ,
,  ; г)
; г)  ,
, 
 .
.
5. Найти дисперсии величин 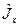 ,
,  ,
,  в состояниях а)
в состояниях а)  ,
,  ; б)
; б)  ,
,  ; в)
; в)  ,
, 
 .
.
6. Доказать соотношение  , где
, где  - матрица Паули,
- матрица Паули,  - произвольный вещественный параметр,
- произвольный вещественный параметр, 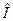 - единичная матрица.
- единичная матрица.
7. Покажите, что любую матрицу второго порядка можно разложить по четырем линейно независимым матрицам: 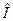 (единичная матрица),
(единичная матрица),  ,
,  и
и 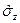 (матрицы Паули).
(матрицы Паули).
8. Частица находится в состоянии  . Определите вероятности различных значений проекции момента на направление, составляющее угол
. Определите вероятности различных значений проекции момента на направление, составляющее угол  с осью
с осью 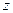 .
.
9. Получить явный вид операторов  в прямоугольных декартовых, сферических и цилиндрических координатах.
в прямоугольных декартовых, сферических и цилиндрических координатах.
Приближенные методы решения задач квантовой механики
10. Вариационным методом найти энергию основного и первого возбужденного уровней частицы в бесконечно глубокой одномерной потенциальной яме, аппроксимируя собственные функции гамильтониана простейшими полиномами, удовлетворяющими требуемым условиям (граничные условия, условие нормировки, ортогональность волновых функций основного и первого возбужденного состояний).
11. Используя вариационный метод, найдите энергию основного состояния атома гелия. Оба электрона находятся в 1s-состоянии. Пробную функцию для вариационного расчета выберите в виде  , где a - вариационный параметр, r1(2) – расстояние между 1 (2) электроном и ядром. Ядро считайте бесконечно тяжелым.
, где a - вариационный параметр, r1(2) – расстояние между 1 (2) электроном и ядром. Ядро считайте бесконечно тяжелым.
12. Показать, что поправка первого порядка  к энергетическим уровням частицы в бесконечно глубокой одномерной потенциальной яме для непрерывного гладкого возмущения
к энергетическим уровням частицы в бесконечно глубокой одномерной потенциальной яме для непрерывного гладкого возмущения  не зависит от n при n>>1.
не зависит от n при n>>1.
13. Для заряженного линейного осциллятора найти сдвиги энергетических уровней в однородном электрическом поле, направленном вдоль оси колебаний, в первых двух порядках теории возмущений. Гамильтониан невозмущенного осцилллятора 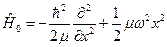 , оператор возмущения
, оператор возмущения  . Сравнить результат с точным решением этой задачи (можно получить из решения для невозмущенного осциллятора заменой переменных).
. Сравнить результат с точным решением этой задачи (можно получить из решения для невозмущенного осциллятора заменой переменных).
14. На двухуровневую систему (уровни невырожденные, их энергии e1 и e2) накладывается возмущение, характеризуемое матричными элементами V11, V22, V12 = V21* между исходными невозмущенными состояниями 1 и 2. Найти вид матрицы возмущенного гамильтониана в энергетическом представлении (представлении собственных функций невозмущенного гамильтониана  .
.
15. Найти сдвиги уровней в первых двух порядках теории возмущений, указать условия применимости полученных результатов и сравнить их с точными. Точные результаты можно получить, используя результат задачи 3.
16. Вычислить в первом приближении теории возмущений сдвиг энергетического уровня основного состояния водородоподобного атома или иона, обусловленный неточечностью ядра.
17. Вычислите в первом порядке теории возмущений энергию основного состояния двухэлектронного атома или иона с зарядом ядра Z, принимая в качестве возмущения взаимодействие электронов между собой. Указание: воспользуйтесь формулой 
Кроме того, учтите соотношения ортогональности:  .
.
18. Найдите в низшем неисчезающем порядке теории возмущений поправки к энергетическим уровням линейного гармонического осциллятора, обусловленные возмущением вида а)  ; б)
; б)  , где a - некоторая константа. Получите условие малости поправок с сравните его с классическим условием ангармоничности колебаний.
, где a - некоторая константа. Получите условие малости поправок с сравните его с классическим условием ангармоничности колебаний.
19. Система обладает только двумя стационарными состояниями 1 и 2 с энергиями  и
и  ,
,  . В момент времени t = 0, когда система находилась в основном состоянии, было включено не зависящее от времени возмущение W. Вычислить вероятность обнаружения системы в том или ином из ее возможных состояний в момент времени t.
. В момент времени t = 0, когда система находилась в основном состоянии, было включено не зависящее от времени возмущение W. Вычислить вероятность обнаружения системы в том или ином из ее возможных состояний в момент времени t.
20. Гамильтониан системы зависит от некоторого параметра l так, что  , где
, где  и
и  от l уже не зависят. Покажите, что
от l уже не зависят. Покажите, что  , где Е0(l) – основной уровень этого гамильтониана.
, где Е0(l) – основной уровень этого гамильтониана.
21. Гамильтониан системы, состоящей из двух подсистем, имеет вид 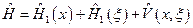 , где
, где  и
и  - координаты первой и второй подсистем,
- координаты первой и второй подсистем,  - оператор взаимодействия между подсистемами. Считая характерные частоты 1-й («быстрой») подсистемы много большими характерных частот 2-й («медленной») подсистемы, свести задачу приближенного вычисления энергетических уровней и соответствующих им волновых функций совокупной системы к решению уравнений Шредингера для отдельных подсистем. На основе полученных результатов в первом порядке адиабатического приближения исследуйте основное состояние молекулярного иона
- оператор взаимодействия между подсистемами. Считая характерные частоты 1-й («быстрой») подсистемы много большими характерных частот 2-й («медленной») подсистемы, свести задачу приближенного вычисления энергетических уровней и соответствующих им волновых функций совокупной системы к решению уравнений Шредингера для отдельных подсистем. На основе полученных результатов в первом порядке адиабатического приближения исследуйте основное состояние молекулярного иона 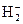 , состоящего из двух протонов и одного электрона.
, состоящего из двух протонов и одного электрона.
22. Определить в борновском приближении амплитуду рассеяния, дифференциальное и полное сечение рассеяния в полях а)  ; б)
; б)  ; в)
; в)  ; г)
; г)  ; д)
; д) 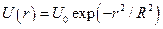 ; е)
; е)  ; ж)
; ж)  . Здесь
. Здесь  ,
,  . Исследовать предельные случаи медленных и быстрых частиц. Указать условия применимости результатов. Рассматривать случай
. Исследовать предельные случаи медленных и быстрых частиц. Указать условия применимости результатов. Рассматривать случай  .
.
23. Определить в квазиклассическом приближении коэффициент прохождения частицы под потенциальным барьером при условии  , где
, где  - энергия частицы,
- энергия частицы, 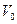 - высота барьера.
- высота барьера.
24. Частицы падают на потенциальный барьер при условии  . Определить в квазиклассическом приближении вероятность отражения частиц от барьера.
. Определить в квазиклассическом приближении вероятность отражения частиц от барьера.
При расчетах можно использовать MathCad и др.