МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ ПО ВЫПОЛНЕНИЮ ДОМАШНЕЙРАБОТЫ

Рекомендации по выполнению задания 5-6. Принятие решений экономического характера может осуществляться в одной из трех ситуаций: в условиях определенности, риска, и неопределенности.

Первая ситуация имеет место в том случае, если можно с приемлемой точностью предсказать однозначно трактуемые последствия принятого решения.

В условиях риска поле возможных исходов, т.е. последствий принятого решения, вариабельно, однако значения исходов и вероятности их появления поддаются количественной оценке.

В условиях неопределенности подобной оценки сделать уже нельзя, т.е. не могут быть перечислены все возможные исходы и/или заданы их вероятности.

В ситуациях 1 и 2 возможные последствия (исходы), сопутствующие каждому варианту решения, известны, но отсутствуют вероятности наступления исходов, т. е. налицо условия неопределенности.

Данные, необходимые для принятия решения в условиях неопределенности, обычно задаются в форме таблицы выплат, строки которой соответствуют возможным действиям (управленческим решения) А_i, а столбцы - возможным состояниям «природы» S_j.

Пусть S_j — состояние «природы», при этом j = , где n - число возможных состояний. Все возможные состояния известны, не известно только, какое состояние будет иметь место в условиях, когда планируется реализация принимаемого управленческого решения. Будем считать, что множество управленческих решений (альтернатив) А_i также конечно и равно m. Реализация А_iплана в условиях, когда «природа» находится в состоянии S_j, приводит к определенному результату, который можно оценить, введя количественную меру -выплата.

В качестве этой меры – выплаты- могут служить

-выигрыши от принимаемого решения (выбираемой альтернативы) – прибыть, доход, доходность. В задачах перед такими выплатами ставится знак плюс «+»;

-затраты, расходы, убытки, потери от принимаемого решения. Такие элементы в задачах имею знак минус;

-полезность, риск и другие количественные критерии.

Таблица выплат может быть представлена в следующем виде:

Альтернативы (варианты управленческих решений) (А_i)	Состояние среды (S_j)
S₁	S₂	……..	S_n
А₁	x₁₁	x₁₂	……..	x_1n
А₂	x₂₁	x₂₂	……..	x_2n
……..	……..	……..	……..	……..
А_m	x_m1	x_m₂	……..	x_mn

Следовательно, математическая модель задачи принятия решений в условиях неопределенности определяется множеством состояний природы S_j, множеством планов (стратегий) А_i и таблицей выплат.

Таблицу можно свернуть в матрицу выплат Х = ||x_ij||, где i – номер строки матрицы выплат, т. е. варианта решений (альтернативы), j – номер столбца матрицы, т. е. состояние природы.

Помимо матрицы выплат в отдельных задачах строят и используют матрицы рисков.

Наличие выплат, являющихся показателями эффективности при различных состояниях среды, позволяет определить потери в результате принятия неоптимальных решений – в случае, когда ожидаемое состояние среды не наступило. Для обозначения потерь вводится специальный показатель, который называется риском. Риск - мера несоответствия между разными возможными результатами принятия определенных стратегий (действий). Он демонстрирует, насколько выгодна применяемая нами альтернатива при конкретном состоянии среды с учетом степени ее неопределенности. Величина риска – это размер платы за отсутствие информации о состоянии среды.

Используя показатель риска, расчет которого осуществляется на основании таблицы (матрицы) выплат, можно построить таблицу (матрицу) риска R =||r_ij|| или таблицу (матрицу) упущенных возможностей.

Элементы матрицы рисков r_ij связаны с элементами матрицы выплат следующим соотношением:

r_ij = β_j – x_ij,

где β_j = 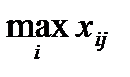- максимальный элемент в столбце j матрицы выплат.

Риском r_ij при выборе альтернативы А_i и при состоянии среды S_j называют разность между выплатой, которую можно получить, зная, что состояние среды будет S_j и выплатой, которая будет получена при отсутствии такой информации. То есть риск r_ij – это разность между максимальной выплатой и выплатой по конкретной альтернативе при данном состоянии среды.

Матрица рисков дает более наглядную картину неопределенной ситуации, чем матрица выплат.

Например, для матрицы выплат

β₁= 6, β₂= 8, β₃ = 5, β₄ = 9.

Согласно введенным определениям r_ij и β_j получаем матрицу рисков

К числу классических критериев, которые используются при принятии решений в играх с природой, можно отнести критерии максимакса, Вальда(максимина), Сэвиджа (минимакса), Гурвица, Лапласа.

Критерий максимакса. Позволяет определить стратегию, максимизирующую максимальные выплаты для каждого состояния среды. Это критерий крайнего оптимизма. При использовании этого критерия игрок рискует, выбирает из матрицы выплат максимальный элемент сначала по строкам, а затем из выбранных максимальных выбирает опять максимальный:

К = ,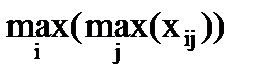

где х_ij – элемент матрицы выплат ||x_ij|| (i – номер строки, j – номер столбца).

Запись вида означает поиск максимума перебором строк, а запись вида – поиск максимума перебором столбцов.

Максиминный критерий Вальда называют критерием крайнего пессимизма (консервативного игрока), т. к. при его использовании предполагается, что от любого решения надо ожидать худших последствий и поэтому надо выбрать такое решение, при котором худший из результатов будет относительно лучше других. Для этого необходимо сначала выбрать в строках матрицы минимальные элементы, а затем из выбранных минимальных выбрать один максимальный. По местонахождению выбранного элемента(i) определить вариант решения:

К = .

Таким образом, из всех самых неудачных результатов выбирается лучший.

Максимин считается фундаментальным критерием. К нему надо прибегать в случаях, когда ошибки в выборе стратегии поведения могут привести к катастрофическим последствиям, а также когда решение можно принять только один-единственный раз и в последующем его изменить уже не удастся.

Критерий минимаксного риска Сэвиджа – ориентирован не столько на минимизацию потерь, сколько на минимизацию сожалений по поводу упущенной прибыли. Он допускает разумный риск ради получения дополнительной прибыли. Выбор стратегии аналогичен выбору стратегии по принципу Вальда с тем отличием, что игрок руководствуется не матрицей выплат, а матрицей рисков R=||r_ij||.

При использовании критерия Сэвиджа обеспечивается наименьшее значение максимальной величины риска:

К =

В исходной матрице выплат принятие решений с использованием критерия Сэвиджа предполагает выполнение следующих действий:

1.определить лучший результат каждого отдельного столбца:

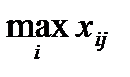2. определить отклонения от лучших результатов в пределах каждого отдельного столбца, т. е.

Получаем матрицу отклонений или матрицу сожалений (матрицу риска).

3. для каждой строки матрицы сожалений находим наибольшую величину

4. выбираем то решение, при котором максимальное сожаление будет меньше других максимальных сожалений:

К = .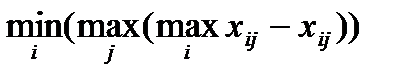

Критерий пессимизма-оптимизма Гурвица. Этот критерий основан на следующих двух предположениях: «природа» может находиться в самом невыгодном состоянии с вероятностью ρ и в самом выгодном состоянии с вероятностью (1- ρ), где ρ — коэффициент пессимизма.

Сначала для каждой строки матрицы определяются максимальный и минимальный элементы, затем они складываются с назначенными коэффициентами значимости (также для каждой строки), из рассчитанных значений выбирается максимальное, соответствующее i-й строке. По нему и определяется i-й вариант решения:

К = ,

Критерий Гурвица устанавливает баланс между случаями крайнего пессимизма и крайнего оптимизма путем взвешивания обоих способов поведения соответствующими весами ρ и (1 — ρ).

Коэффициент ρ может принимать значения от 0 до 1, в зависимости от склонности лица, принимающего решение, к пессимизму или к оптимизму. Если он подходит к ней оптимистически, то величина ρ должна быть меньше 0,5. При пессимистической оценке ситуации игрок должен взять ρ больше 0,5. При отсутствии ярко выраженной склонности ρ = 0,5 представляется наиболее разумной.

Так как параметр ρ берется довольно произвольно, то и выбор с помощью критерия Гурвица не свободен от субъективизма.

При ρ =0 критерий Гурвица совпадает с максимаксным критерием, а при ρ = 1 - с критерием Вальда.

Критерий Лапласа. Этот критерий опирается на «принцип недостаточного основания»_Лапласа, согласно которому все состояния «природы» S_jj = полагаются равновероятными. В соответствии с этим принципом каждому состоянию S_j ставится вероятность р_j определяемая по формуле

Оптимальной является та альтернатива, которой соответствует наибольшая ожидаемая сумма выплат, т.е.

А^* =

Выбор критерия принятия решений в условиях неопределенности является наиболее сложным и ответственным этапом. При этом не существует каких-либо общих советов или рекомендаций. Выбор критерия должно производить лицо, принимающее решение (ЛПР), с учетом конкретной специфики решаемой задачи и в соответствии со своими целями, а также опираясь на прошлый опыт и собственную интуицию.

В частности, если даже минимальный риск недопустим, то следует применять критерий Вальда. Если, наоборот, определенный риск вполне приемлем и ЛПР намерено вложить в некоторое предприятие столько средств, чтобы потом оно не сожалело, что вложено слишком мало, то выбирают критерий Сэвиджа.

Пример. Компания “Российский сыр” – производитель продуктов из сыров, определяет, сколько ящиков сыра производить каждый месяц. В течение месяца спрос может принимать значение 6, 7, 8 или 9 ящиков. Затраты на производство 1 ящика 45 дол., а цена продажи – 95 дол. В случае непродажи ящика в конце месяца он списывается как испорченный.

Сколько ящиков сыра следует производить каждый месяц? Для принятия решения использовать критерии максимакса, Вальда, Сэвиджа и Гурвица (положите ρ = 0,5).

Р е ш е н и е. Строим таблицу выплат. Альтернативами или стратегиями компании являются различные показатели числа ящиков с сыром, которые ему, возможно, следует производить. Состояниями природы выступают величины спроса на аналогичное число ящиков. По условию, спрос на сыр может колебаться от 6 до 9 ящиков, поэтому компании целесообразно производить от 6 до 9 ящиков сыра.

Элементы таблицы выплат – это прибыль, которую получит компания в зависимости от выбранной альтернативы и спроса. Поэтому перед элементами ставим знак «+».

Рассчитаем прибыль. Компания производит 6 ящиков и спрос 6 ящиков. Выручка в этом случае 570 дол. (6 * 95 дол.), издержки – 270 дол. (6*45 дол), прибыль 300 дол.(570 – 270). В случае, если спрос составит 7, 8 или 9 ящиков, а произведено только 6 ящиков, объем продаж составит 6 ящиков и прибыль будет одна и та же 300 дол.

Компания производит 7 ящиков, а спрос 6 ящиков. Прибыль от указанного сочетания спроса и предложения будет равна 6 * 95 – 7*45=255 дол. Прибыль при том же объеме производства и спросе 7 (8, 9) ящиков составит 7*95-7*45=350 дол.

Аналогично проводятся расчеты при других сочетаниях спроса и предложения. В итоге получим следующую платежную матрицу:

Производство ящиков	Спрос на сыр

Далее модифицируем таблицу следующим образом:

Производство ящиков	Спрос на ящики	Max в строке	Min в строке





Критерий				максимакс	максимин
мах в столбце

1.По критерию максимакса следует производить 9 ящиков.

2. По критерию Вальда (максимин)- 6 ящиков.

3. Критерию Сэвиджа (минимакс). Определяем максимальное значение в каждом столбце. Строим матрицу сожалений, используя формулу:

maxX_ij - X_ij

Для каждой строки матрицы сожалений находим наибольшую величину. Получаем столбец максимумов сожалений. Выбираем решение, при котором максимальное сожаление меньше других максимальных сожалений, т. е находим минимальное значение из максимальных значений сожалений. Решение оформим в виде таблицы:

Производство ящиков	Спрос на ящики	Max в строке





Критерий			Сэвидж

Для данной задачи по критерию Сэвиджа следует производить 8 ящиков.

4. Критерий Гурвица.

i=1 6 ящиков H₁ = = 0,5*300+0,5*300=300

i=2 7 ящиков H₂ = 0,5*255+0,5*350= 302,5

i=3 8 ящиков H₃ = 0,5*210+0,5*400= 305

i=4 9 ящиков H₄ = 0,5*165+0,5*450= 307,5

Так как К = , то следует производить 9 ящиков.

Выбор критерия для принятия решения определяется руководителем.

Рекомендации по выполнению задания7. В задаче для оценки риска и принятия решения следует использовать статистический метод приятия решений. Его основные инструменты:

Среднее ожидаемое значение (математическое ожидание):

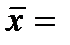∑(р_i_* х_i) = ,

где р_i – вероятность свершения события х;

n – число случаев наблюдения события i;

х_i - ожидаемое значение.

Колеблемость (изменчивость) возможного результата – представляет собой степень отклонения ожидаемого значения от средней величины. Для расчета на практике обычно применяют два близко связанных критерия: дисперсия и среднее квадратическое отклонение.

Дисперсия определяется по формуле:

D(х) =σ²= ,

где n – число случаев наблюдения (частота);

– математическое ожидание (среднее ожидаемое значение).

Среднее квадратическое отклонение определяется по формуле

σ =

Дисперсия и среднее квадратическое отклонение - это показатели абсолютной колеблемости.

Для анализа обычно используют относительный показатель - коэффициент вариации:

V= σ/ *100%

Коэффициент вариации может изменяться от 0 до 100%. Чем больше коэффициент, тем сильнее колеблемость. Установлена следующая качественная оценка различных значений коэффициента вариации:

· До 10% - слабая колеблемость;

· 10-25% - умеренная колеблемость;

· свыше 25%– высокая колеблемость.

При принятии решения выбирается тот вариант, где коэффициент вариации меньше.

Пример. Пусть имеются два инвестиционных проекта. Первый с вероятностью 0,6 обеспечивает прибыль 15 млн. руб., однако с вероятностью 0,4 можно потерять 5,5 млн. руб. Для второго проекта с вероятностью 0,8 можно получить прибыль 10млн. руб. и с вероятностью 0,2 потерять 6 млн. руб. Какой проект выбрать?

Р е ш е н и е. Оба проекта имеют одинаковую среднюю прибыльность, равную 6,8 млн. руб. (0,6 *15+0,4 (-5,5)=0,8 * 10 + 0,2 * (-6) = 6,8). Однако среднее квадратическое отклонение для первого проекта равно 10,04 млн. руб. ([0,6 (15 –6,8)²+0,4(-5,5-6,8)²]^1/2=10,04), а для второго – 6,4 млн. руб.([0,8(10-6,8)²+0,2(-6-6,8)²]^1/2=6,4), поэтому предпочтительнее второй проект.

Это же подтверждает расчет коэффициента вариации. Для первого проекта он равен 1,5 (10,4/6,8), а для второго 0,94 (6,4/6,8). Выбирается тот вариант, где коэффициент вариации меньше.

Рекомендации по выполнению задания8. Дерево решений – графическое изображение последовательности решений и состояний среды с указанием соответствующих вероятностей и выплат для любых комбинаций альтернатив и состояний среды (исходов).

Дерево решений создается при движении слева направо, а анализируется в обратном направлении. При создании дерева пункты принятия решений (ППР) обозначаются квадратами, а узлы возникающих неопределенностей (УВН) – кружками. Для разветвления неопределенности рассчитывается вероятность, а в конце каждой финальной ветви указывается ожидаемая выплата. При обратном анализе для каждого узла неопределенности рассчитывается математическое ожидание. Для каждого пункта принятия решений выплата максимизируется. Лучшее решение выбирается по максимуму выплат.

Сущность Байесовского подхода заключается в систематическом применении формулы Байеса для решения прикладных задач на основе концепции субъективной вероятности. Формула Байеса позволяет уточнить первоначальную вероятность интересующего нас суждения на основании дополнительной информации о появлении или не появлении события, как-либо связанного с нашим суждением. Такое уточнение позволяет принимать более правильное решение.
После составления "дерева решений" производится его обратный анализ (справа налево), в ходе которого на место УВН ставятся математические ожидания выплат, а на место ППР максимальные значения тех величин, которые находятся на окончаниях ветвей, исходящих из ППР. Эти максимумы указывают направление принятия лучших решений.

Схема использования формулы Байеса для анализа дерева решений.

Высказывается некоторое суждение (гипотеза Н1) и определяется вероятность ее истинности Р (Н1). Затем выбивается некоторое событие А, связанное по вероятности с гипотезой Н1. Если последняя верна, то вероятность события А равна Р(А/Н1). Полная же вероятность события А в любом случае, независимо от истинности или ложности гипотезы Н1, равна Р(А).

Если поступает информация о наступлении события А, то первоначальная вероятность истинности гипотеза Н1 уточняется следующим образом:

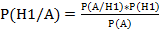(1)

где Р(Н1/А) – уточненная вероятность гипотезы Н1; Р(Н1) – ее первоначальная вероятность.

Если в последующем поступит новая порция информации, например о событии В, тоже связном вероятностью Р(В/Н1) с гипотезой Н1, то уточненная на базе наступления этих двух событий вероятность гипотезы Н1 будет вычислена так:

(2)

Здесь Р(АВ) – полная вероятность совместного наступления сразу двух событий А и В.

Приведенную формулу (2) называют «двойным Байесом».

Тогда, дерево решений – графическое изображение последовательности решений и состояний среды с указанием соответствующих вероятностей и выплат для любых комбинаций альтернатив и состояний среды (исходов).

Схема использования формулы Байеса для анализа дерева решений.

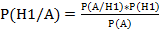(1)

где Р(Н1/А) – уточненная вероятность гипотезы Н1; Р(Н1) – ее первоначальная вероятность.

(2)

Здесь Р(АВ) – полная вероятность совместного наступления сразу двух событий А и В.

Приведенную формулу (2) называют «двойным Байесом».

МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ ПО ВЫПОЛНЕНИЮ ДОМАШНЕЙРАБОТЫ

Поиск по сайту