Qlnorm(c(0.025,0.975), ep1,ep2)
[1] 1.932985e-04 7.632626e+05
Потенциальные выбросы (за пределами интервала)
ind<-(x < x.q95[1] | x > x.q95[2])
x[ind]
[1] 1.251784e-04 6.582054e+06
Классические критерии
2.1. Стьюдента, независимые выборки
Для правильного применения критерия Стьюдента необходимо убедиться в однородности дисперсий, и нормальности распределений в классах.
head(p)
x group
1 13.684232 2
2 4.233953 1
3 2.779204 1
4 4.586447 1
5 12.864484 1
| Проверка на нормальность | Сравнение дисперсий | Сравнение средних (Критерий Стьюдента) | |
| group=1 | Нормальное, pval=0.148 | Дисперcии Равны: pval=0.419 | Средние Равны t=0.9, pval=0.346 |
| group=2 | Нормальное, pval=0.455 |
2.2.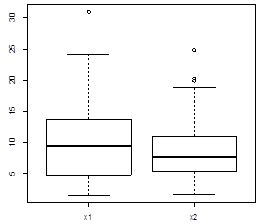 
Стьюдента, парная выборка
head(p)
x1 x2
1 22.220731 8.312812
2 4.542273 16.987173
3 3.614630 5.369026
4 23.848382 6.969115
5 13.773307 6.665310
| Проверка на нормальность распределения разности(x1-x2) | Сравнение средних (Критерий Стьюдента), парная выборка | |
| x1 | Нормальное, p.value=0.933 | Средние Равны t=1.5, pval=0.147 |
| x2 |
Средние выборок статистически равны.
2.3. Колмогорова-Смирнова, сравнение с заданным распределением
p<-read.table("task-2.3-01_norm_mean_15.0_sd_7.dat",header=F)
ks.test(x,pnorm,15,7)
D = 0.1656, p-value = 0.1991 >0.05
В данном случае нет оснований отвергнуть гипотезу о принадлежности выборки к заданному (norm(15;7)) распределению.
2.4. 
Фишера, сравнение 2 дисперсий
x group
1 3.743656 1
2 5.052694 2
3 4.471285 2
4 7.479095 1
5 22.743478 1
| Проверка на нормальность | Сравнение дисперсий, var.test | |
| group1 | Нормальное, pval=0.25 | Дисперcии Равны: pval=0.988 |
| group2 | pval=0.05, будем считать, что нормальное |
2.5. Однородность нескольких дисперсий (Бартлетта).
x group
1 14.872935 3
2 15.809697 1
3 3.688286 3
4 15.418776 4
5 2.859019 2
| bartlett.test | |
| x1 | Дисперсии однородны K-squared = 3.4018, df = 3, p-value = 0.3337 |
| x2 | |
| x3 | |
| x4 |
2.6. Однородность нескольких дисперсий (Флигнера-Килина).
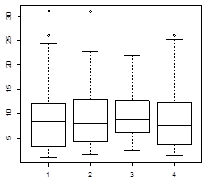Критерий Флигнера-Килина не требует предположений о нормальности сравниваемых выборок.
Fligner-Killeen:med chi-squared = 3.8293,
df = 3,
p-value = 0.2805
Дисперсии однородны.
2.7. 
Однородность нескольких дисперсий (Кокрана).
Cochran test for outlying variance
data: x ~ group
C = 0.32477,
df = 40, k = 4,
p-value = 0.277
Дисперсии однородны.
2.8. 
Ранговый критерий Уилкоксона-Манна-Уитни (сравнение с константой).
Wilcoxon signed rank test with continuity correction
data: p$V1
V = 571, p-value = 0.524
alternative hypothesis: true location is not equal to 6
Т.о нельзя сказать, что данные статистически отличаются от заданной константы.
2.9. Ранговый критерий Уилкоксона-Манна-Уитни (сравнение средних двух выборок).
Wilcoxon rank sum test with continuity correction
W = 1109, p-value = 0.3476
alternative hypothesis:
true location shift is not equal to 0
Т.о нет статистически значимых различий
между средними групп.
Оценка значимости корреляции (линейной и монотонной). (Lab03).
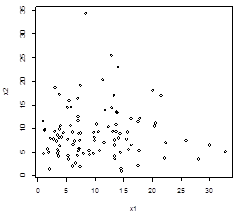
| Тест | Корреляция | p-value | Отличие от нуля статистически: |
| spearman | 0.030 | 0.767 | не значимо |
| kendall | 0.022 | 0.743 | не значимо |
| pearson | 0.010 | 0.920 | не значимо |
Полученные коэффициенты статистически не отличаются от нуля, значит зависимости между x1 и x2 нет.
Линейная модель, функция lm(), (Lab04, Lab05). Зависимая переменная y, независимый переменные скаляр x1 и фактор g1. Построить модель от переменных и их взаимодействий.
4.1. Протокол построения линейной модели, выбор оптимальной модели, и оценки ее адекватности.
Модели:
p.lm0<-lm(y~1,data=p)
p.lm1<-lm(y~x1,data=p)
p.lm2<-lm(y~x1+g1,data=p)
p.lm3<-lm(y~x1*g1,data=p)
Для выбора модели рассчитаем критерий Акаика, и выполним сравнение вложенных моделей с помощью ANOVA.
| Модель | AIC | RSS | ANOVA p-value |
| p.lm0 | 562.1 | 1554.23 | |
| p.lm1 | 414.2 | 347.13 | < 0.001 |
| p.lm2 | 314.6 | 125.68 | < 0.001 |
| p.lm3 | 286.5 | 92.96 | < 0.001 |
drop1(p.lm3,test="F")
Single term deletions
Model:
y ~ x1 * g1
Df Sum of Sq RSS AIC F value Pr(>F)
<none> 92.958 0.6977
x1:g1 1 32.722 125.680 28.8569 33.793 7.999e-08 ***
Коэффициенты регрессии значимы. Т.о выбираем модель lm3.
Процедуры диагностики моделей множественной регрессии
(для выбранной lm3):
а)остатки против модели б) распределение остатков в сравнении с нормальным
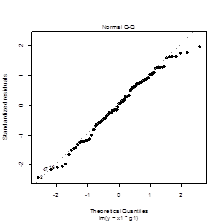
в) равномерность дисперсии остатков
|
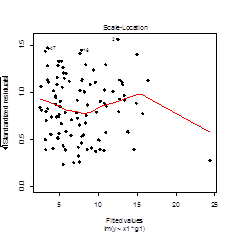
Отсутствие зависимости остатков от переменныхPавномерность дисперсии остатков
Наблюдается небольшая нелинейность зависимости остатков от переменных, дисперсии равномерны относительно фактора, что в целом соответствует предположению.
В результате модель Lm3 считаем адекватной (остатки распределены нормально, и не зависят от предикторов модели, выраженные нелинейные зависимости отсуствуют).
Дисперсионный анализ (Lab03, Lab04).
5.1.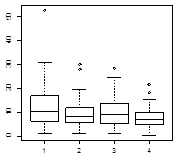 
Метод Краскела-Уоллиса.
Kruskal-Wallis rank sum test
data: x by group
Kruskal-Wallis chi-squared = 4.8982,
df = 3,
p-value = 0.1794
Сравниваемые группы статистически значимо не различаются.
5.2. Метод Тьюки.
Tukey multiple comparisons of means
95% family-wise confidence level
Fit: aov(formula = x ~ as.factor(group), data = p)
$`as.factor(group)`
diff lwr upr p adj
2-1 0.847990013 -3.350721 5.046701 0.9530666 #разницы нет
3-1 0.843687200 -3.355024 5.042398 0.9537294 #разницы нет
4-1 -0.547096239 -4.745807 3.651615 0.9866124 #разницы нет
3-2 -0.004302813 -4.203014 4.194408 1.0000000 #разницы нет
4-2 -1.395086252 -5.593797 2.803625 0.8239427 #разницы нет
4-3 -1.390783439 -5.589495 2.807928 0.8252805 #разницы нет
Видно, что во всех случаях разницы между парами нет p adj>0.05
5.3. Дисперсионный анализ в рамках линейной модели, выбираем aov()+summary() или lm()+anova().
а)Дисперсионный анализ (ANOVA)
H0: μ1 = μ2 = μ3
anova(lm(x~ as.factor(group), data = p))
Pr(>F)= 0.9876 фактор group не оказали существенного влияния на x.
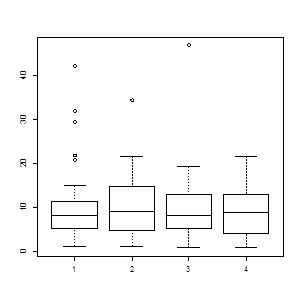
Видно, что разброс групповых средних в целом меньше, чем разброс значений в экспериментальных группах. Фактор group не оказали существенного влияния на x.
б)M<- aov(x~ as.factor(group), data = p)
summary(M)
Pr(>F)= 0.988 – полученное значение многим превышает 5%-ный уровень значимости и, на этом основании, мы заключаем, что нулевая гипотеза верна, и фактор group не оказали существенного влияния на x.