Тема: Решение тригонометрических уравнений
Дата: 02.03.2021 г.
Группа: ПК-261
Цели урока:
Образовательные:
o углубление понимания методов решения тригонометрических уравнений;
o сформировать навыки различать, правильно отбирать способы решения тригонометрических уравнений.
Воспитательные:
o воспитание познавательного интереса к учебному процессу;
o формирование умения анализировать поставленную задачу;
o способствовать улучшению психологического климата в классе.
Развивающие:
o способствовать развитию навыка самостоятельного приобретения знаний;
o способствовать умению учащихся аргументировать свою точку зрения;
Ход урока.
1. Актуализация опорных знаний.
Изучение нового материала
Продолжим изучение способов решения тригонометрических уравнений
Уравнения вида a sin x + b cos x = 0, где a и b – некоторые числа, называются однородными уравнениями первой степени относительно sin x или cos x.
1. Рассмотрим уравнение
sin x – cos x = 0. Разделим обе части уравнения на cos x. Так можно сделать, потери корня не произойдёт, т.к., если cos x = 0, то sin x = 0. Но это противоречит основному тригонометрическому тождеству sin 2 x + cos 2 x = 1.
Получим tg x – 1 = 0.
tg x = 1,
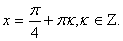
Ответ: 
2. Уравнения вида a sin 2 x + bcos 2 x + c sin x cos x = 0, где a, b, c – некоторые числа, называются однородными уравнениями второй степени относительно sin x или cos x.
Рассмотрим уравнение
sin2x – 3 sin x cos x + 2 cos2= 0. Разделим обе части уравнения на cos x, при этом потери корня не произойдёт, т.к. cos x = 0 не является корнем данного уравнения.
tg2x – 3tg x + 2 = 0.
Пусть tg x = t. D = 9 – 8 = 1.
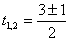тогда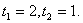 
Отсюда tg x = 2 или tg x = 1.
В итоге x = arctg 2 +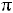 
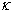, x =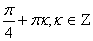 
Ответ: arctg 2 + ,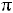
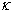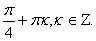
3. Рассмотрим ещё одно уравнение: 3 sin2x – 3 sin x cos x + 4 cos2x = 2.
Преобразуем правую часть уравнения в виде 2 = 2 · 1 = 2 · (sin2x + cos2x). Тогда получим:
3sin2x – 3sin x cos x + 4cos2x = 2 · (sin2x + cos2x),
3sin2x – 3sin x cos x + 4cos2x – 2sin2x – 2 cos2x = 0,
sin2x – 3sin x cos x + 2cos2x = 0. (Получили 2 уравнение, которое уже разобрали).
Ответ: arctg 2 + 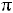k,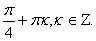
4.Решение линейных тригонометрических уравнений
Линейным тригонометрическим уравнением называется уравнение вида
a sin x + b cos x = с, где a, b, c – некоторые числа.
Рассмотрим уравнение sin x + cos x = – 1.
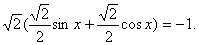Перепишем уравнение в виде:
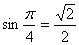Учитывая, что и, получим:
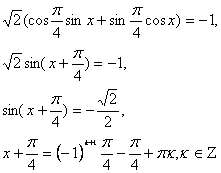
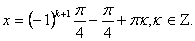
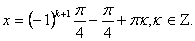
Ответ:
5.Введение дополнительного аргумента
Выражение a cos x + b sin x можно преобразовать:
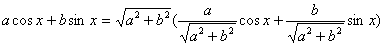
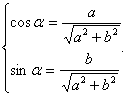(это преобразование мы уже ранее использовали при упрощении тригонометрических выражений)
Введём дополнительный аргумент – угол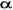 
такой, что
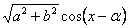
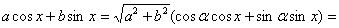Тогда
=
Рассмотрим уравнение: 3 sinx + 4 cosx = 1
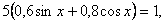Учтём, что 
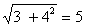. Тогда получим
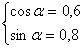0,6 sin x + 0,8 cosx = 1. Введём дополнительный аргумент – угол 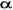такой,
что, т.е. 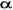= arcsin 0,6. Далее получим
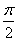
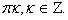Ответ: – arcsin 0,8 + +
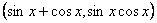6.Уравнения вида Р
Такого рода уравнения удобно решать при помощи введения вспомогательной переменной t = sin x ± cosx. Тогда 1 ± 2 sinx cosx = t2.
Решить уравнение: sinx + cosx + 4 sinx cosx – 1 = 0.
Введём новую переменную t = sinx + cosx, тогда t2 = sin2x + 2sin x cos x + cos2 =
1 + 2 sin x cos x Откуда sin x cos x =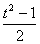 
. Следовательно получим:
t + 2 (t2– 1) – 1 = 0.
2 t2+ t – 2 – 1 = 0,
2 t2+ t – 3 = 0..Решив уравнение, получим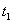 
= 1,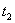 
= 
.
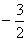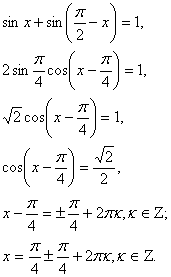sinx + cosx = 1 или sinx + cosx =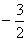
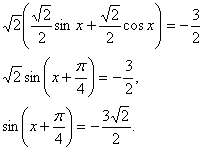
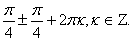Корней нет.
Ответ:
7. Решение уравнений, содержащих тригонометрические функции под знаком радикала.
Решить уравнение: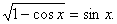 
В соответствии с общим правилом решения иррациональных уравнений вида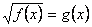 
, запишем систему, равносильную исходному уравнению: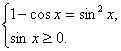 
Решим уравнение 1 – cos x = 1 – cos2x.
1 – cos x = 1 – cos2x,
1 – cos x – (1 – cos x) (1 + cos x) = 0,
(1 – cos x) (1 – 1 – cos x) = 0,
– (1 – cos x) cos x = 0.
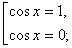
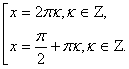
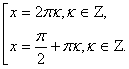
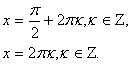
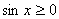Условию удовлетворяют только решения
Ответ: 
8.Решение уравнений с использованием ограниченности тригонометрических функций y = sin x и y = cos x.
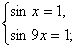
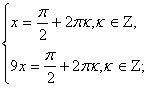
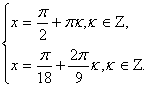Решить уравнение: sin x + sin 9x = 2.
Так как при любых значениях х sin x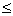 
1, то данное уравнение равносильно системе:
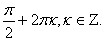Решение системы
Ответ: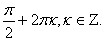
Итог урока
Таким образом мы сегодня рассмотрели 8 различных способов решения тригонометрических уравнений. Безусловно, многие из приведённых задач могут быть решены несколькими способами.
Домашнее задание
1. § 36 стр.192 «Алгебра и начала математического анализа 10-11» Ш.А.Алимов
№621 (2,4), №623 (2)
2. а также всем желающим индивидуальное творческое задание:
найти различные способы решения тригонометрического уравнения
sinx + cosx = 1
Критерии оценивания:
Оценка «отлично» - выставляется обучающемуся, если правильно решены все задания, выполнены в полной мере, изложены логично.
Оценка «хорошо» - выставляется обучающемуся, если допущены незначительные погрешности в задании.
Оценка «удовлетворительно» - выставляется обучающемуся, если ответ на вопрос нелогичный, не полный.
Оценка «неудовлетворительно» - выставляется обучающемуся, если задания не решены.
ВНИМАНИЕ!!!
Уважаемые студенты, практическое задание необходимо выполнить в рабочей тетради (сфотографировать) или в формате Документа Word. Отправлять для проверки в личные сообщения на страницу ВКонтакте: https://vk.com/kolomiyetssg?z=photo95751036_324720501%2Falbum95751036_0%2Frev
Преподаватель: Коломиец Светлана Григорьевна