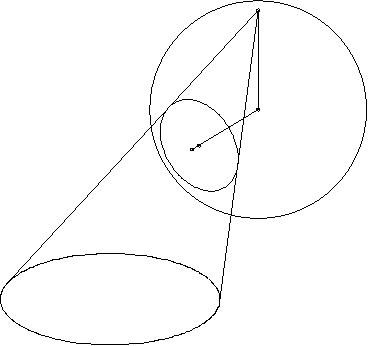
Пусть прямая а касается окружности α в точке S, а точка N диаметрально противоположна точке S. Проведем окружность ω с центром N и радиусом NS. При инверсии относительно ω окружность α переходит в прямую а. Проведем в окружности α диаметр МК, параллельный прямой а, и рассмотрим точки А1 и А2 симметричные относительно этого диаметра. При инверсии точки А1, А2, М переходят в точки В1, В2, Р. Докажем, что SB1 · SB2 = SP2.
Для доказательства заметим, что углы ÐNSA2 и ÐSNA1 симметричны относительно оси МК, и, следовательно равны. Угол ÐSA2N опирается на диаметр, поэтому SA2 – высота прямоугольного треугольника NSВ2. Отсюда получаем, что ÐNSA2 = ÐSNA1 = ÐNSВ2, значит треугольники NSB1 и NSB2 подобны. SB2 / NS = NS / SB1, следовательно SB1 · SB2 = NS2.
Осталось заметить, что треугольник NSP прямоугольный и равнобедренный. NS = SP. Отсюда следует справедливость формулы SB1 · SB2 = SP2.
Теперь будем вращать чертеж относительно оси NS. Окружность α превратится в сферу с диаметром NS, прямая а будет при вращении заметать плоскость, а точка Р начертит на этой плоскости окружность ω с центром S.
Рассмотрим отображение сферы на плоскость, называемое стереографической проекцией. Каждой точке сферы соответствует ее проекция на плоскость из точки N (северного полюса), самой точке N соответствует бесконечно удаленная точка круговой плоскости. То есть, при таком отображении бесконечно удаленная точка, которая была введена как некоторый абстрактный элемент, находит свое место на сфере, как центр стереографической проекции.
Заметим, что точкам сферы А1 и А2, симметричным относительно плоскости, параллельной плоскости проекции, соответствуют на плоскости проекции точки В1, В2, симметричные относительно окружности ω. Значит, инверсии на плоскости соответствует при стереографической проекции зеркальная симметрия на сфере.
Стереографическую проекцию можно также истолковать, как результат инверсии пространства относительно подходящей сферы. Для этого надо сначала определить, что такое инверсия пространства и установить какими свойствами она обладает.
Здесь, к счастью, дело обстоит очень просто. Достаточно лишь заменить во всех формулировках, относящихся к инверсии плоскости, слова «окружность» и «прямая» на слова «сфера» и «плоскость». Доказательства соответствующих теорем практически не изменятся. Если еще добавить к пространству одну «бесконечно удаленную точку», считая ее образом центра любой инверсии, а плоскость считать сферой, проходящей через «бесконечно удаленную точку», то можно установить справедливость следующей теоремы:
Теорема 1''
При инверсии пространства образом сферы является сфера.
Заметим, что стереографическая проекция возникает, как результат инверсии пространства относительно сферы с центром N. При этом, сфере, проходящей через центр инверсии, соответствует плоскость. Это простое соображение позволяет доказать важнейшее свойство стереографической проекции.
Теорема 7
Стереографическая проекция переводит окружность на сфере в окружность на плоскости.
Для доказательства заметим лишь, что две пересекающиеся сферы (или сфера и плоскость) пересекаются по окружности. Вместе с теоремой (1'') получаем, таким образом, что при инверсии пространства окружности переходят в окружности.
Поскольку стереографическая проекция получается как результат инверсии пространства, то справедливость теоремы можно считать установленной.
Последняя теорема представляет еще один пример утверждения, которое легко и естественно доказывается с помощью инверсии, однако превращается в весьма трудную задачу, если пользоваться только «школьными» методами.
Задача 15
Рассмотрим произвольную окружность на сфере. Как определить инверсию сферы относительно окружности? (то есть отображение сферы на себя, обладающее свойствами инверсии)
Стереографическая проекция, несмотря на свои замечательные свойства, редко находит применение в школьном курсе математики, однако удалось отыскать сложную задачу, которая быстро и красиво решается с использованием доказанных теорем.
Назовем гексаэдром многогранник с шестью четырехугольными гранями, которые сходятся по три в каждой вершине. Таким образом, у гексаэдра шесть граней, восемь вершин и двенадцать ребер. Примерами гексаэдров в школьном курсе служат параллелепипеды и усеченные четырехугольные пирамиды. Однако можно рассматривать гексаэдры самого общего вида, не накладывая каких-либо дополнительных условий на их грани и ребра. Следующая задача не имеет отношения к инверсии, но представляет самостоятельный интерес.
Задача 16
Три четырехугольника на плоскости имеют общую вершину и три общих стороны, выходящих из этой вершины. Рассматривая их как параллельную проекцию трех смежных граней некоторого гексаэдра, построить проекцию трех остальных граней.
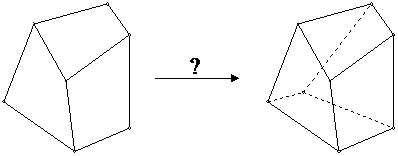
Теперь рассмотрим произвольный(!) гексаэдр, вписанный в сферу. Докажем следующее утверждение:
Задача
Если семь вершин гексаэдра лежат на сфере, то и восьмая вершина лежит на этой сфере.
Доказать эту теорему обычными «метрическими» средствами весьма нелегко (если вообще возможно), поскольку произвольный гексаэдр не обладает никакими «хорошими» свойствами. Поэтому, займемся сначала «переводом задачи на другой язык».
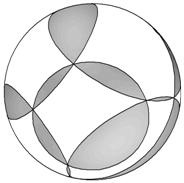Рассмотрим сечения сферы плоскостями граней гексаэдра. Получим шесть окружностей на сфере. Каждая окружность пересекается с четырьмя другими, а всего у них восемь общих точек, в каждой из которых встречаются по три окружности. Точнее, по условию общих точек – семь, а наличие восьмой требуется доказать.
Рассмотрим стереографическую проекцию сферы на плоскость с центром в какой-либо вершине. Тогда три окружности, проходящих через центр проекции, перейдут в три прямые на плоскости, а три других окружности – в три окружности на плоскости.
Одной вершины – центра проекции, на чертеже нет, она «ушла в бесконечность». Оставшиеся точки, прямые и окружности образуют чертеж к хорошо известной задаче.
Пусть на сторонах треугольника взяты три произвольные точки. Три окружности, каждая из которых проходит через вершину треугольника и две смежные с ней точки, пересекаются в одной точке.
Для доказательства достаточно провести две окружности и соединить точку их пересечения с тремя точками на сторонах. Как известно, вокруг четырехугольника можно описать окружность, тогда и только тогда, когда сумма его противоположных углов равна 180°.
Обозначив углы треугольника a, b, g (a + b + g = 180°), получаем, что два угла при точке пересечения равны 180° – a и 180° – b. На третий угол остается:
360° – (180° – a) – (180° – b) = a + b = 180° – g,
Значит, третий четырехугольник также вписан в окружность, что и доказывает утверждение задачи.
Здесь можно, пожалуй, остановиться, хотя тема инверсии, или более широко, геометрии окружностей далеко не исчерпана. Можно упомянуть задачу Аполлония о построении окружностей, касающихся трех данных, или задачу Мальфатти о построении трех попарно касающихся окружностей, вписанных в треугольник.
 |
Не рассмотрена также такая естественно возникающая конструкция, как пучки окружностей и многое другое. (ссылка на литературу)