Рассматривается двумерная модель химического реактора идеального вытеснения по веществу (продольный и поперечный коэффициенты диффузии равны нулю) и полного продольного перемешивания по энергии (продольный коэффициент теплопроводности равен бесконечности, а поперечный имеет конечное значение).
Стационарные уравнения массотеплопереноса для рассматриваемой модели реактора в безразмерной форме имеют вид
 (2.19)
(2.19)
 (2.20)
(2.20)









Здесь С, С  - концентрация ключевого вещества в реакторе и на входе в реактор соответственно, Т, Т
- концентрация ключевого вещества в реакторе и на входе в реактор соответственно, Т, Т  - температура в реакторе и температура поступающей смеси, h - теплота реакции,
- температура в реакторе и температура поступающей смеси, h - теплота реакции,  и с плотность и удельная теплоемкость смеси реагентов и продуктов реакции,
и с плотность и удельная теплоемкость смеси реагентов и продуктов реакции,  - газовая постоянная,
- газовая постоянная,  - предэкспонент Аррениуса, l и a длина и радиус реактора, и - скорость смеси, X и R - продольная (
- предэкспонент Аррениуса, l и a длина и радиус реактора, и - скорость смеси, X и R - продольная (  ) и поперечная (
) и поперечная (  ) координаты,
) координаты,  - объёмная доля смеси реагентов и продуктов реакции в пористом слое катализатора,
- объёмная доля смеси реагентов и продуктов реакции в пористом слое катализатора,  - значение эффективного коэффициента теплопроводности в радиальном направлении, g - параметр, пропорциональный числу Дамклера.
- значение эффективного коэффициента теплопроводности в радиальном направлении, g - параметр, пропорциональный числу Дамклера.
Уравнения (2.19), (2.20) дополняются граничными условиями (2.15-2.17).
х = 0  (2.15)
(2.15)
r = 0  (2.16)
(2.16)
r = 1 
 (2.17)
(2.17)
Стационарное распределение степени продвижения реакции определяется решением уравнения (2.19) с граничным условием (2.15).



Стационарное распределение степени продвижения реакции связано с радиальным распределением температуры соотношением
 (2.21)
(2.21)
Подставляя (2.21) в (2.20), получаем для определения стационарного распределения температуры по радиусу реактора уравнение
 (2.22)
(2.22)
где  (2.23)
(2.23)
Число решений двухточечной краевой задачи (2.22), (2.16) и определяет количество стационарных режимов работы реактора. В силу нелинейности функции  может быть несколько стационарных режимов.
может быть несколько стационарных режимов.
Решение задачи (2.20), (2.16) найдено методом малого параметра при Ре<<1, что соответствует случаю, когда тепло распространяется по радиусу значительно быстрее, чем сносится потоком вдоль реактора.
Распределение температуры в реакторе ищется в виде
 (2.24)
(2.24)
И тогда для определения неизвестных функций  (i=0,1,2,…) получается последовательность линейных задач
(i=0,1,2,…) получается последовательность линейных задач
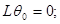 r = 0;
r = 0; 

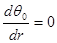 (2.25)
(2.25)
 r = 0;
r = 0;  r = 1;
r = 1; 

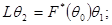 r = 0;
r = 0;  r = 1;
r = 1; 
 ,
,  ,
, 
Система уравнений (2.25) обладает тем свойством, что константы предыдущего приближения определяются в процессе нахождения следующего приближения.
Нулевое приближение решения имеет вид
 (2.26)
(2.26)
Их физический смысл легко определить значения  определяются из алгебраического уравнения (2.26), представляющего собой равенство тепловыделения и теплоотвода в модели полного перемешивания.
определяются из алгебраического уравнения (2.26), представляющего собой равенство тепловыделения и теплоотвода в модели полного перемешивания.
Для конечных значений числа Пекле задачу (2.20), (2.16) аналитически решить не удается.
Результаты численных расчетов приведены на рис. 2 для параметров 

В случае а) для значений параметров 

 при разных значениях
при разных значениях  решение оказалось единственным.
решение оказалось единственным.
В случае б), когда 

 ; решений три. Они хорошо аппроксимируются аналитической оценкой показанной штриховой линией.
; решений три. Они хорошо аппроксимируются аналитической оценкой показанной штриховой линией.
Приведенные данные показывают, что стационарное распределение температуры в реакторе хорошо описывается параболой, которая становится круче с увеличением чисел Пекле и Био.
3.
Численный алгоритм решения задачи
Рассматривается двумерная модель химического реактора с продольным и поперечным перемешиванием в случае больших чисел Пекле, рассчитываемых по коэффициенту эффективной теплопроводности в поперечном направлении, то есть анализируется предельный случай модели, когда тепло распространяется в поперечном направлении значительно медленнее, чем сносится потоком вдоль реактора.
В рассматриваемой двумерной модели химического реактора предполагается идеальное вытеснение по веществу (продольный и поперечный коэффициенты диффузии равны нулю) и полное продольное перемешивание по энергии.
На рисунках 3.1-3.3 приведены расчеты профилей температуры по r при значениях числа Пекле, равного 0,01; 0,1; 1, и при этом значениях числа Био, равного 0,1 (см. Рис. 3.1); 1 (см. Рис. 3.2); 10 (см. Рис. 3.3), температура теплоносителя  = 0,1, а температура поступающей смеси
= 0,1, а температура поступающей смеси  = 1,5.
= 1,5.

Рис. 3.1. Распределение профиля температуры по r при значении числа Bio=0,1

Рис. 3.2. Распределение профиля температуры по r при значении числа Bio=1

Рис. 3.3. Распределение профиля температуры по r при значении числа Bio=10
Из рисунков 3.1-3.3 видно, что с увеличением числа Пекле профили температуры быстрее выравниваются по радиусу, увеличение числа Био (0.1; 1; 10;) приводит к более резкому изменению температурного профиля в окрестности стенки реактора.
Заключение
псевдоожиженный массоперенос теплоотвод тепло
В данной курсовой работе был сделан аналитический обзор моделей теплообмена в химических реакторах с псевдоожиженным слоем. Построена стационарная модель тепло-массопереноса для различных условий теплоотвода через стенку реактора.
В результате проделанной работы были получены следующие результаты:
1) Моделирование тепло-массопереноса в реакторе с псевдоожиженным слоем;
2) Численное решение уравнений диффузии и теплопроводности;
) Проведение численных расчетов профилей температуры методом прогонки;
) Сравнение результатов численного расчета с известными результатами.
Список источников
1. Патанкар, С.В. Численное решение задач теплопроводности и конвективного теплообмена при течении в каналах / С.В. Патанкар. - Пер. с англ. Е.В. Калабина; под. ред. Г.Г. Янькова. - М.: Изд-во МЭИ, 2003. - 312 с.
2. Кузнецов, Г.В. / Разностные методы решения задач теплопроводности: учебное пособие / Г.В. Кузнецов, М.А. Шеремет. - Томск: Изд-во ТПУ, 2007. - 172 с.
. Д. Перлмуттер, Устойчивость химических реакторов, Л.: Химия, 1967, 328 с.
. А.А. Самарский, Ю.П. Попов, Разностные методы решения задач газовой динамики, М.: Наука, 1980, 352 с.