№ 1. Определить длину отрезка АВ.
Рис. 26
Если отрезок параллелен плоскости проекций, то его длина определяется длиной проекции отрезка на этой плоскости. Поэтому для решения задачи построим дополнительную ортогональную проекцию отрезка на плоскости, параллельной этому отрезку или проходящей через него и перпендикулярной к одной из плоскостей проекций.
Строим дополнительную ортогональную проекцию А4В4 отрезка АВ на плоскости П4 проходящей через отрезок и перпендикулярной к плоскости П1. Ось Х14 совпадает с горизонтальной проекцией А1В1 отрезка АВ. Ось Х12 проведена через фронтальную проекцию А2 точки А. Расстояние от оси Х14 до дополнительных проекций А4 и В4 точек А и В равно расстоянию от фронтальных проекций точек А2 и В2 этих точек до оси Х12. Длина дополнительной ортогональной проекции А4В4 отрезка АВ на плоскости проекций П4 равна длине отрезка АВ (рис.27).
Рис.27
№ 2. Определить расстояние от точки А до прямой l.
Рис. 28
Расстояние от точки до прямой определяется длиной отрезка перпендикуляра, опущенного из точки на прямую.
На эпюре проекции перпендикуляра к прямой можно построить, если прямая параллельна плоскости проекций. Поэтому сначала строим дополнительную ортогональную проекцию прямой l и точки А на плоскости проекций П4, параллельной прямой l и перпендикулярной к плоскости П1. При этом ось Х14 параллельна l 1. Для построения дополнительной проекции прямой l на ней отмечены точки 1 и 2. Проводим дополнительную проекцию А4К4 перпендикуляра (А4К4 ^ l 4),а затем строим горизонтальную проекцию перпендикуляра А1К1 и его фронтальную проекцию А2К2. По двум проекциям отрезка АК(А1К1 и А2К2) находим его длину путём поворота вокруг фронтально проецирующей оси i, проходящей через точку А, до положения параллельного плоскости П1. Длина отрезка А1К¢1 и есть расстояние от точки А до прямой l (рис.29).
Рис.29
№ 3. Определить расстояние от точки А до плоскости a(h Çf).
Рис.30
Расстоянием от точки до плоскости является длина отрезка перпендикуляра, опущенного из точки на плоскость.
Из точки А проведём перпендикуляр n к плоскости a(h Çf) - (n2 ^ f2, n1 ^ h1) и построим точку К, в которой перпендикуляр n пересекает плоскость a. Построение выполняется с помощью прямой t, лежащей с перпендикуляром n в одной фронтально проецирующей плоскости.
Длина отрезка перпендикуляра АК определяется аналогично длине отрезка АВ в задаче № 5.1, основная ось Х12 проведена через точку К2, а дополнительная ось Х14 совпадает с n1. Полученный отрезок А4К4 на плоскости П4 измеряет расстояние от точки А до плоскости a(рис.31).
Рис.31
№ 4. Определить расстояние между скрещивающимися прямыми l и m, l ^ П1 и m - прямая общего положения.
Рис. 32
Под расстоянием между скрещивающимися прямыми понимается длина отрезка перпендикуляра, общего для обеих прямых.
Если одна из скрещивающихся прямых l перпендикулярна к плоскости проекций П1, то их общий перпендикуляр АВ параллелен плоскости проекций П1. При этом прямой угол между перпендикуляром и прямой m проецируется на плоскости П1 в прямой угол, и проекция отрезка перпендикуляра А1В1 между прямыми l и m определяет расстояние между ними (рис33).
Рис.33
№ 5. Определить расстояние между скрещивающимися прямыми h и f; h ççП1 и f ççП2
Рис. 36
Обе прямые h и f занимают положение линий уровня. Для перехода к задаче № 5.4 вводим дополнительную плоскость проекций П4 ^ П1 и П4 ^ h, ось Х14 перпендикулярна к h1. Длина проекции А4В4 отрезка АВ общего перпендикуляра прямых h и f равна искомому расстоянию, так как отрезок АВ параллелен плоскости проекций П4 (рис.37).
Рис37.
№ 6. Определить расстояние между двумя параллельными прямыми m и n.
Рис. 38
Перпендикуляр, опущенный из любой точки одной прямой на другую, определяет расстояние между прямыми.
Обе параллельные прямые m и n параллельны плоскости П1. Зададим точку А на прямой m и опустим из этой точки А перпендикуляр на прямую n. Заменим плоскость П2 на плоскость П4 так, чтобы она была перпендикулярна к прямой n. Новая ось Х14 проведена перпендикулярно к проекции n1 прямой n. На линиях связи от новой оси Х14 откладываем отрезки, равные расстояниям от заменяемых проекций А2 и n2, точки А и прямой n, до оси Х12.
Получим проекцию А4 точки А и проекцию n 4 прямой n.
Расстояние между А4 и n 4 и будет искомым(рис.39)
Рис.39
№ 7. Определить расстояние от точки А до плоскости
a(m ççn)^П2.
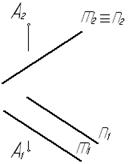Рис. 40
Плоскость a (m ççn)является фронтально проецирующей. Перпендикуляр, опущенный из точки А на плоскость a, параллелен плоскости проекций П2 и длина проекции его отрезка на этой плоскости проекций П2 равна искомому расстоянию (рис.41).
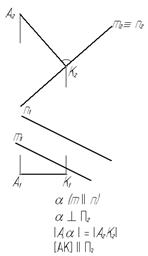
Рис.41
№ 8. Определить расстояние между двумя параллельными плоскостями a (а ççb) и β (с Ça), a Ùβ ^П2.
Рис. 42
Решение этой задачи можно свести к определению расстояния от точки К, взятой в плоскости a до другой плоскости β. См. решение задачи № 7(рис.43).
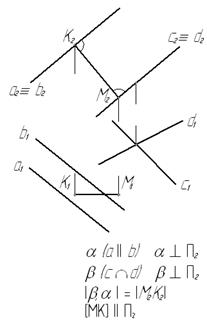
Рис.43
№ 9. Определить угол между пересекающимися прямыми l и m.
Рис. 44
Отмечаем в плоскости a(l Ç m) горизонталь h и поворачиваем плоскость вокруг горизонтали h в положение горизонтальной плоскости. При этом точки 1 и 2, принадлежащие горизонтали, остаются неподвижными. Точка А перемещается по окружности, плоскость которой перпендикулярна к горизонтали. На плоскость П1 окружность проецируется в отрезок прямой, перпендикулярной к горизонтальной
проекции h1 горизонтали h. Проводим через горизонтальную проекцию А1 точки А прямую, перпендикулярную к h1, и отмечаем точку О1, в которой она пересекает h1. Точка О1 - горизонтальная проекция центра О окружности, по которой перемещается точка А. Его фронтальная проекция О2 принадлежит h2. Отрезки О1A1 и О2А2 - горизонтальная и фронтальная проекции радиуса RA указанной окружности.
Находим длину радиуса RA, для чего строим дополнительную ортогональную проекции О4А4 отрезка ОА на плоскости П4, проведенный через отрезок ОА и перпендикулярной к П1.Отложив отрезок О4А4 на прямой О1А1 и от точки О1, находим горизонтальную проекцию А¢1 точки А после поворота. Соединив точку А¢1 с точками 11 и 21, получаем проекции l ¢1 и m¢1 прямых l и m после поворота. Угол j° между ними равен искомому углу(рис45).
Рис.45
№ 10.Определить угол между скрещивающимися прямыми h и f.
Рис.46
Угол между скрещивающимися прямыми равен углу между пересекающимися прямыми, параллельными заданным скрещивающимся прямым.
Через точку А на прямой h проводим прямую l, параллельную прямой f. Теперь решение задачи сводится к определению угла между пересекающимися прямыми h и l.
Угол j° между пересекающимися прямыми h и l находим поворотом плоскости, образованной прямыми h и l вокруг фронтали l этой плоскости до положения фронтальной плоскости. Отмечаем на горизонтали h точку В (В1,В2) и поворачиваем точку В вокруг фронтали l до положения В¢2 и угол между прямыми l 2 и h¢2 =j°- есть искомый угол между прямыми h и f(рис.47).
Рис.47
№ 11. Определить угол между прямой l и плоскостью a (n Ç f)
Рис. 48 Рис. 49
Углом между прямой и плоскостью считается угол между этой прямой и её ортогональной проекцией на данную плоскость. Исходя из этого, решение задачи может быть следующим. Из произвольной точки М прямой l опускаем перпендикуляр n на плоскости a. Находим точку пересечения этого перпендикуляра с плоскостью (точка Мa) и точку К пересечения прямой l с плоскостью a. Через точки К и Мa проводим прямую l a - проекцию прямой l на плоскости a. Угол j° между прямыми l и l a - искомый угол.
Решение задачи упрощается, если определить угол ω° (угол между прямой l и перпендикуляром n). Зная угол ω°, определим искомый угол j°=90° - ω°. Для построения перпендикуляра n, на эпюре n1 строится перпендикулярно к h1, а n2 строится перпендикулярно к f2. Угол ω° между прямой l и перпендикуляром определяется поворотом плоскости этого угла вокруг горизонтали h*. См. решение задачи № 5.9. Угол j° получается дополнением угла ω° до 90°(рис50).
Рис.50
№ 12. Определить угол между плоскостями a (а Ç b) и β (с Ç d).
Рис.51 Рис.52
Угол между двумя плоскостями равен углу между перпендикулярами к этим плоскостям.
Из произвольной точки пространства К(К1, К2) проведены перпендикуляры t (t1 ^ a1, t2 ^ b2) к плоскости a(а Ç b) и q(q1 ^ c1, q2 ^ d2) к плоскости β(с Ç d). Плоскость перпендикуляров t и q повернута вокруг фронтали f(f1, f2) до положения фронтальной плоскости. Фронтальные проекции t¢2 и q¢2 повернутых перпендикуляров t и q образуют угол j°, равный искомому углу между двумя плоскостями a и β(рис.53).
Рис.53
№ 13. Определить углы наклона отрезка АВ к плоскостям проекций П1 и П2.
Рис.54
Для решения задачи взята новая плоскость П4, отвечающая двум условиям: П4 ^ П1 и П4÷÷АВ. В системе П4 / П1 прямая АВ стала параллельна плоскости П4, а поэтому Х14÷÷А1В1. На плоскость П4 без искажения проецируется и отрезок АВ и угол a°, угол между прямой АВ и плоскостью проекций П1. А чтобы определить угол между прямой АВ и плоскостью проекций П2, введем ещё одну дополнительную плоскость проекций П5, отвечающую тоже двум условиям: П5^П2 и П5÷÷АВ. В системе П5 / П2 прямая АВ становится параллельна плоскости П5, и поэтому Х25÷÷А2В2. На плоскость П5 без искажения проецируется и отрезок АВ, и угол β°, угол между прямой АВ и плоскостью проекций П2 (рис.55).
Рис.55
№ 14. Определить углы наклона плоскости a(а÷÷ b) к плоскостям проекций П1 и П2.
Рис. 56
Плоскость a общего положения задана двумя параллельными прямыми а и b. Для решения поставленной задачи нужно новую плоскость проекций расположить перпендикулярно a и одной из плоскостей проекций. Вот почему в заданной плоскости проводим горизонталь и фронталь. Эти линии уровня нужны для ориентировки новых плоскостей проекций П4 и П5. Расположив П4 ^ h (горизонтали плоскости), обеспечиваем выполнение двух условий: новая плоскость П4 будет перпендикулярна и П1, и плоскости a, новую ось Х14 проводим под прямым углом к h1 (горизонтальной проекции горизонтали). Новая проекция плоскости a представляет собой прямую линию a4. На плоскость П4, которая перпендикулярна плоскости a и плоскости П1, без искажения проецируется угол a, Ù П1, образованный плоскостью a с плоскостью П1.
Для определения угла, образованного плоскостью a с плоскостью проекций П2, вводим ещё одну дополнительную плоскость П5 так, чтобы П5 ^ П2 и П5 ^ a нужно расположить П5 ^ f (фронтали плоскости). На эпюре ось Х25 проводим под прямым углом к f2 (фронтальной проекции фронтали). Проекция плоскости a представляет собой прямую линию a5. На плоскости П5, которая перпендикулярна плоскости a и плоскости П2, без искажения проецируется угол a,Ù П2, образованный плоскостью a с плоскостью П2 (рис.57)
Рис.57
№ 15. Определить натуральный вид треугольника АВС.
. 
Рис. 58
Такая задача может быть решена или путём построения дополнительных ортогональных проекций АВС, или путём поворота плоскости этого треугольника вокруг линии уровня в положение соответствующей плоскости уровня.
Если задаться целью: одним поворотом расположить треугольник параллельно плоскости П1, то за ось вращения следует принять горизонталь (А-1). В тот момент, когда плоскость треугольника будет параллельна П1, горизонтальные проекции каждой из перемещающихся вершин окажутся удаленными от оси вращения на расстоянии, равное радиусу вращения данной точки.
Дальнейшие построения выполняются в такой последовательности:
1) проводим прямые, перпендикулярные А1 - 11, по которым будут перемещаться горизонтальные проекции вращающихся точек;
2) строим проекции радиуса вращения одной из них, например В. Это будут отрезки В1О1 и В2О2;
3) по двум проекциям определяем истинную величину радиуса вращения RB (см. решение задачи № 1);
4) отрезок RB откладываем от точки О той прямой, по которой перемещается горизонтальная проекция вершины В;
5) через полученную точку В¢1 и неподвижную 11 проводим прямую до пересечения с прямой, по которой перемещается горизонтальная проекция вершины С;
6) соединяя найденные точки В¢1 и С¢1 друг с другом и с неподвижной вершиной А1, получаем новую горизонтальную проекцию треугольника.
Эта проекция и определяет натуральную величину ∆ АВС.
Фронтальная проекция треугольника окажется преобразованной в прямую, которая совпадает с h2 (А2 -12)(рис.59)
Рис.59
№ 16. Определить угол j° между плоскостями a(∆ АВС) и β(∆АВD).
Рис. 60
Углу между двумя плоскостями соответствует линейный угол между прямыми, по которым данные плоскости пересекаются третьей плоскостью, перпендикулярной к линии их пересечения.
Линия пересечения двух заданных плоскостей a и β есть горизонталь АВ. Чтобы определить угол j° между плоскостями a и β, введем новую дополнительную плоскость П4 ^ АВ. На эпюре новая ось Х14 проводится перпендикулярно к А1В1; плоскость П4, перпендикулярная АВ, будет параллельна сторонам линейного угла, которым измеряется двугранный угол j°(рис.61).
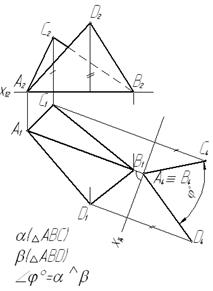
Рис.61