Рассмотрим функцию поиска вершины в АВЛ-дереве с включением вершины в АВЛ-дерево в случае ее отсутствия:
void Search (int x, node **p)// x - ключ вершины, помещаемой в АВЛ-дерево.// *p - указатель на корень АВЛ-дерева.// h - флаг, сигнализирующий об увеличении высоты поддерева:// TRUE - высота поддерева увеличилась, // FALSE - высота поддерева не увеличилась.// При первом обращении к функции Search() h=FALSE.{ node *p1, *p2; h = FALSE; if (*p==NULL) { // Вершины в дереве нет; включить ее... *p = new(node); h = TRUE; (**p).Key = x; (**p).Count = 1; (**p).Left = (**p).Right = NULL; (**p).bal = 0; // Вершине присвоили нулевой баланс. } else if (x<=(**p).Key) { Search (x,&((**p).Left)); // Вершина уже включена в дерево. if (h==TRUE) // Если высота поддерева увеличилась, // то выросла левая дуга. switch ((**p).bal) { case 1: (**p).bal = 0; h = FALSE; break; // Предыдущая несбалансированность уравновесилась. case 0: (**p).bal = -1; break; // Вес "склонился" влево. case -1: //Балансировка. p1 = (**p).Left; if ((*p1).bal==-1) {//Однократный LL-поворот. (**p).Left = (*p1).Right; (*p1).Right = *p; (**p).bal = 0; *p = p1; } else {//Двукратный LR-поворот. p2 = (*p1).Right; (*p1).Right = (*p2).Left; (*p2).Left = p1; (**p).Left = (*p2).Right; (*p2).Right = *p; //Пересчет баланса вершины с указателем p. if ((*p2).bal==-1) (**p).bal = 1; else (**p).bal = 0; // Пересчет баланса вершины с указателем p1. if ((*p2).bal==1) (*p1).bal = -1; else (*p1).bal = 0; *p = p2; } (**p).bal = 0; h = FALSE; break; } } else //... иначе выросла правая дуга. if (x>(**p).Key) { Search (x,&((**p).Right)); // Вершина уже включена в дерево. if (h==TRUE) // Если высота поддерева увеличилась, // то выросла правая дуга. switch ((**p).bal) { case -1: (**p).bal = 0; h = FALSE; break; case 0: (**p).bal = 1; break; case 1: //Балансировка. p1 = (**p).Right; if ((*p1).bal==1) { //Однократный RR-поворот. (**p).Right = (*p1).Left; (*p1).Left = *p; (**p).bal = 0; *p = p1; } else { //Двухкратный RL-поворот. p2 = (*p1).Left; (*p1).Left = (*p2).Right; (*p2).Right = p1; (**p).Right = (*p2).Left; (*p2).Left = *p; // Пересчет баланса вершины с указателем p. if ((*p2).bal==1) (**p).bal = -1; else (**p).bal = 0; //Пересчет баланса вершины с указателем p1. if ((*p2).bal==-1) (*p1).bal = 1; else (*p1).bal = 0; *p = p2; } (**p).bal = 0; h = FALSE; break; } }}1.Запустите IDE Borland C++ 5.02. Подготовьте запуск исполнимых файлов в консольном режиме.
2.Откомпилируйте и запустите предложенную программу, построения АВЛ-дерева с помощью функции поиска с включением.
#include<iostream.h>#define TRUE 1#define FALSE 0struct node{ int Key; int Count; int bal; node *Left; node *Right;}; class TREE { private: int h; node *Tree; public: TREE () { Tree=NULL; h=FALSE;} void Search (int, node **); void Vyvod (node **, int); node** GetTree() {return &Tree;}}; void main (){ TREE A; int el,i; int n; cout<<"Количество вершин в дереве: "; cin>>n; cout<<"Информационные поля вершин дерева: \n"; for (i=1; i<=n; i++) { cin>>el; A.Search (el,A.GetTree());} cout<<"АВЛ-дерево:\n"; A.Vyvod (A.GetTree(),0);} void TREE::Search (int x, node **p)// x - ключ вершины, помещаемой в АВЛ-дерево.// *p - указатель на корень АВЛ-дерева.// h - флаг, сигнализирующий об увеличении высоты поддерева:// TRUE - высота поддерева увеличилась, // FALSE - высота поддерева не увеличилась.// При первом обращении к функции Search() h=FALSE.{ node *p1, *p2; h = FALSE; if (*p==NULL) { *p = new(node); h = TRUE; (**p).Key = x; (**p).Count = 1; (**p).Left = (**p).Right = NULL; (**p).bal = 0; } else if (x<=(**p).Key) { Search (x,&((**p).Left)); if (h==TRUE) switch ((**p).bal) { case 1: (**p).bal = 0; h = FALSE; break; case 0: (**p).bal = -1; break; case -1: p1 = (**p).Left; if ((*p1).bal==-1) { (**p).Left = (*p1).Right; (*p1).Right = *p; (**p).bal = 0; *p = p1; } else { p2 = (*p1).Right; (*p1).Right = (*p2).Left; (*p2).Left = p1; (**p).Left = (*p2).Right; (*p2).Right = *p; if ((*p2).bal==-1) (**p).bal = 1; else (**p).bal = 0; if ((*p2).bal==1) (*p1).bal = -1; else (*p1).bal = 0; *p = p2; } (**p).bal = 0; h = FALSE; break; } } else if (x>(**p).Key) { Search (x,&((**p).Right)); if (h==TRUE) switch ((**p).bal) { case -1: (**p).bal = 0; h = FALSE; break; case 0: (**p).bal = 1; break; case 1: p1 = (**p).Right; if ((*p1).bal==1) { (**p).Right = (*p1).Left; (*p1).Left = *p; (**p).bal = 0; *p = p1; } else { p2 = (*p1).Left; (*p1).Left = (*p2).Right; (*p2).Right = p1; (**p).Right = (*p2).Left; (*p2).Left = *p; if ((*p2).bal==1) (**p).bal = -1; else (**p).bal = 0; if ((*p2).bal==-1) (*p1).bal = 1; else (*p1).bal = 0; *p = p2; } (**p).bal = 0; h = FALSE; break; } }} void TREE::Vyvod (node **w,int l)//Изображение дерева w на экране дисплея// (рекурсивный алгоритм).//*w - указатель на корень дерева.{ int i; if (*w!=NULL) { Vyvod (&((**w).Right),l+1); for (i=1; i<=l; i++) cout<<" "; cout<<(**w).Key<<endl; Vyvod (&((**w).Left),l+1); }}
Приведем пример построения АВЛ-дерева.
Пусть на "вход" функции Search() последовательно поступают целые числа 4,5,7,2,1,3,6. Изобразим процесс "роста" АВЛ-дерева (в скобках указан показатель сбалансированности некоторых вершин)
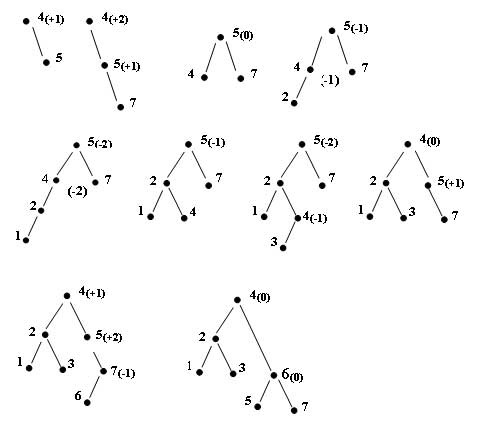
Рис.1. Рост АВЛ-дерева
Тщательно подобранный пример, показывающий ситуацию: как можно больше поворотов при минимальном числе включений!
Оценим эффективность поиска со вставкой, считая, что все вставляемые ключи поступают в случайном порядке. Для этого потребуется ответить на следующие вопросы:
1. Как зависит математическое ожидание значения высоты от общего числа вершин n в дереве?
2. Какова вероятность возникновения случаев, не требующих дополнительной балансировки, случаев, требующих однократного поворота, и случаев, требующих двухкратного поворота, соответственно?
3. Как зависит число операций при вставке одной вершины от длины пути, ведущего из внешней вершины вверх и от числа вершин n в дереве?
До сих пор не удалось дать точных ответов на эти вопросы. Однако сочетание некоторых теоретических рассуждений и эмпирических результатов позволяет сформулировать следующие утверждения.
1. Математическое ожидание значения высоты при больших n близко к значению h = log2n + c. H.Вирт пишет: "Математический анализ этого сложного алгоритма пока не произведен. Эмпирические проверки оправдывают предположение, что ожидаемая высота сбалансированного дерева... равна h=logn+c, где c - малая константа (c ~ 0.25). Это значит, что на практике АВЛ-сбалансированные деревья ведут себя так же, как идеально сбалансированные деревья, хотя с ними намного легче работать".
2. Вероятность того, что при вставке не потребуется дополнительная балансировка, потребуется однократный поворот или двукратный поворот, близка к значениям 2/3, 1/6 и 1/6, соответственно. H.Вирт в своей работе продолжает: "Эмпирически можно предположить, что в среднем балансировка необходима приблизительно один раз на каждые два включения. При этом однократный и двухкратный поворот одинаково вероятны!"
3. Среднее число сравнений при вставке n -го ключа в дерево выражается формулой alog2n+b (a и b - постоянные).
Замечание: трудоемкость удаления вершин из АВЛ-дерева также зависит от числа вершин в дереве как log2n.
Таким образом, АВЛ-дерево представляет собой структуру, для которой любая операция: поиск, вставка и удаление вершины с заданным ключом имеет временную сложность O(log2n).