Глава 7. Статистическое изучение динамики социально-экономических явлений
Методические указания и решение типовых задач
Процессы и явления общественной жизни постоянно изменяются. Эти изменения изучаются в статистике с помощью построения рядов динамики, расчета системы аналитических и средних показателей, выявления основной тенденции (тренда) или сезонности развития общественных явлений.
Рядами динамики называются ряды расположенных в хронологическом порядке показателей, характеризующих изменение размеров общественных явлений во времени.
Ряд динамики состоит из двух основных элементов: во-первых, моментов или периодов времени (t), к которым относятся анализируемые данные; во-вторых, соответствующих им статистических показателей, которые называются уровнями динамического ряда (y).
В зависимости от характера отображаемого явления, а также от вида статистических данных ряды динамики подразделяются на ряды: а) абсолютных, б) относительных и в) средних величин.
В свою очередь, ряды динамики абсолютных величин могут быть представлены либо моментными, либо интервальными (периодическими) рядами.
Если уровни ряда динамики выражают состояние явления на определенные моменты времени, то такие ряды называются моментными рядами динамики. Например, данные о численности населения Республики Беларусь по состоянию на начало года за 2000-2006 гг.
Если уровни ряда динамики характеризуют размеры общественных явлений за определенные интервалы (периоды) времени (за сутки, месяцы, кварталы, годы), то такие ряды называются интервальными (периодическими) рядами динамики. Например, данные об объеме внешней торговли Республики Беларусь по годам за 2000-2005 гг.
Важным условием правильного построения динамических рядов является сопоставимость их уровней. Уровни динамического ряда должны быть сопоставимы с точки зрения одинаковой методологии их расчета для всех периодов и дат; 2) одинаковых единиц измерения; 3) одинаковой полноты охвата различных частей явления и др.
Так как ряды динамики охватывают отдельные, обособленные периоды времени, в течение которых могут происходить изменения, то часто возникает несопоставимость их уровней. Поэтому прежде чем анализировать ряд динамики, необходимо обеспечить сопоставимость его уровней с помощью дополнительных расчетов, то есть произвести так называемое смыкание уровней динамического ряда.
Если несопоставимость в рядах динамики обусловлена административно-территориальными изменениями, то необходимо построить ряд сопоставимых уровней в новых территориальных границах.
Задача 1. Имеются следующие условные данные о производстве картофеля в регионе, тыс. тонн:
| Год | |||||
| В границах региона: | |||||
| старых | 1850,0 | 1930,5 | 2020,0 | ||
| новых | 2444,2 | 2680,9 | 2800,4 |
Решение: Для приведения этих данных к сопоставимому виду определяется коэффициент пересчета для 2004 г. путем соотношения уровней двух рядов: 2444,2/20202,0=1,21.
Умножая на этот коэффициент уровни первого ряда, обеспечивается их сопоставимость с уровнями второго ряда:
2002 г. – 1850,0 · 1,21 = 2238,5 тыс. т
2003 г. – 1930,5 · 1,21 = 2335,9 тыс. т
Таким образом, получен сопоставимый ряд динамики производства картофеля в регионе (в новых границах), тыс. тонн:
| 2002 г. | 2003 г. | 2004 г. | 2005 г. | 2006 г. |
| 2238,5 | 2335,9 | 2444,2 | 2680,9 | 2800,4 |
Несопоставимость уровней интервального динамического ряда может возникать в том случае, если они являются абсолютными величинами и составлены из разновеликих по продолжительности периодов времени. Чаще всего это относится к рядам внутригодовой динамики с месячными и квартальными уровнями.
Задача 2. Имеются следующие фактические данные о продаже молока и молочных продуктов в Республике Беларусь по кварталам 2004 г., тыс. тонн:
| Квартал | І | ІІ | ІІІ | ІV |
| Продано молока и молочных продуктов, тыс. тонн | 336,2 | 340,7 | 342,1 | 359,0 |
Решение: для приведения этого динамического ряда к сопоставимому виду определим размер среднедневной реализации молока и молочных продуктов с учетом числа дней в квартале, тыс. тонн:
1 квартал 336,2/90=3,736
2 квартал 340,7/91=3,744
3 квартал 342,1/92=3,718
4 квартал 359,0/92=3,902
Таким образом, получен ряд динамики сопоставимых уровней продажи молока и молочных продуктов в Республике Беларусь по кварталам 2004 г. (среднедневная реализация), тыс. тонн:
| Квартал | І | ІІ | ІІІ | ІV |
| Среднедневная реализация молока и молочных продуктов, тыс. тонн | 3,736 | 3,744 | 3,718 | 3,902 |
При изучении динамики общественных явлений рассчитывают следующую систему аналитических показателей: абсолютные приросты, темпы роста, темпы прироста и абсолютное значение (содержание) одного процента прироста либо снижения. Расчет этих показателей основан на абсолютном или относительном сравнении уровней динамического ряда. При этом, если каждый уровень сравнивается с его предыдущим уровнем, получают цепные показатели, а если каждый уровень сравнивается с начальным или каким-либо другим, принятым за постоянную базу сравнения (например, уровень, с которого начинается какой-либо новый этап развития явления), то получают базисные показатели динамики.
Абсолютный прирост – это разность двух уровней ряда динамики. Он показывает, на сколько абсолютных единиц данный уровень больше или меньше уровня, взятого для сравнения, и выражается в тех же единицах измерения, что и уровни анализируемого ряда.
Цепной абсолютный прирост (D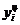 
) исчисляется как разность между сравниваемым уровнем (
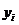) и предшествующим ему уровнем (
):
. 7.1
Базисный абсолютный прирост (
) исчисляется как разность между сравниваемым уровнем и уровнем, принятым за постоянную базу сравнения (y0):
. 7.2
Абсолютный прирост может иметь положительный или отрицательный знак, в последнем случае это не прирост, а снижение.
Сумма цепных абсолютных приростов за определенный период времени равна базисному абсолютному приросту за весь этот период. А разность между анализируемым и предыдущим базисными абсолютными приростами дает соответствующий цепной абсолютный прирост.
Темп роста – это отношение двух уровней ряда динамики. Он выражается в коэффициентах или в процентах. В первом случае он показывает, во сколько раз данный уровень больше или меньше уровня, взятого для сравнения, во втором – сколько процентов данный уровень составляет по отношению к другому уровню, взятому для сравнения.
Цепной темп роста (
) исчисляется как отношение между сравниваемым уровнем и предшествующим ему уровнем:
. 7.3
Базисный темп роста (
) исчисляется как отношение между сравниваемым уровнем и уровнем, принятым за постоянную базу сравнения:
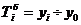7.4
Если темп роста меньше единицы, то имеет место не рост, а снижение (падение) анализируемого уровня.
Последовательное произведение цепных темпов роста за определенный период времени, выраженных в коэффициентах, дает базисный темп роста за этот же период. А отношение анализируемого базисного темпа роста к предыдущему дает соответствующий цепной темп роста.
Темп прироста – это отношение абсолютного прироста к уровню, принятому за базу сравнения. Он обычно выражается в процентах и показывает, на сколько процентов уровень данного периода больше (или меньше) базисного.
Цепной темп прироста (
) равен:
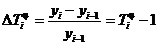7.5
Базисный темп прироста (
) равен:
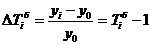7.6
Темп прироста вычисляется и как разность между темпом роста, выраженным в процентах, и 100%:
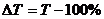7.7
Темп прироста может иметь как положительный, так и отрицательный знак.
Абсолютное значение (содержание) одного процента прироста (снижения) – это отношение цепного абсолютного прироста за анализируемый период (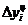
) к соответствующему темпу прироста (), выраженному в процентах:
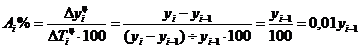7.8
Следовательно, количественно абсолютное значение одного процента равно одной сотой части уровня, предшествующего анализируемому, и выражается в тех же единицах, что и соответствующие уровни.
Задача 3. Динамика производства телевизоров в Республике Беларусь за 2001-2004 гг. характеризуется следующими данными:
| Телевизоры, тыс. шт. |
Проанализируйте динамику производства телевизоров в Республике Беларусь за 2001-2004 гг. с помощью аналитических показателей динамического ряда. Полученные результаты оформите в таблице.
Решение: Рассчитаем цепные абсолютные приросты, используя формулу .
Определим базисные абсолютные приросты, используя формулу , принимая за базу сравнения начальный уровень ряда динамики – 2001 г.
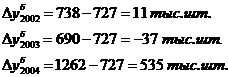
Рассчитаем цепные темпы роста по формуле .
Определим базисные темпы роста по формуле :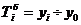
Темпы прироста составят:
цепные
базисные
Абсолютное значение 1% прироста (снижения) рассчитываем цепным способом по формуле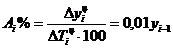 
. Для нашего примера значения данного показателя составят:
.
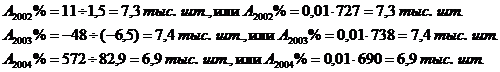Занесем полученные данные в таблицу:
Таблица 7.1 Аналитические показатели динамики производства телевизоров в Республике Беларусь за 2001-2004 гг.
| Годы | Производство телевизоров, тыс. шт. | Абсолютный прирост, тыс. шт. | Темп роста, % | Темп прироста, % | Абсолютное значение 1% прироста, тыс. шт. | |||
| по годам | с 2000 г. | по годам | с 2000 г. | по годам | с 2000 г. | |||
| - | - | - | 100,0 | - | - | - | ||
| 101,5 | 101,5 | 1,5 | 1,5 | 7,3 | ||||
| -48 | -37 | 93,5 | 94,9 | -6,5 | -5,1 | 7,4 | ||
| 182,9 | 173,6 | 82,9 | 73,6 | 6,9 |
Как видно из таблицы, в сравнении с предыдущими периодами производство телевизоров в Республике Беларусь возрастает, причем наибольший прирост – на 572 тыс. шт. или 82,9% - составил в 2004 г. по сравнению с 2003 г. Снижение производства наблюдалось лишь в 2003 г. по сравнению с предыдущим годом – на 6,5% (или 572 тыс. шт.) и по сравнению с 2001 г. – на 5,1% (535 тыс. шт.).
При анализе и сопоставлении рядов динамики, характеризующих социально-экономические явления, рассчитывают коэффициенты опережения. Они представляют собой отношение темпов роста или прироста за одинаковые отрезки времени по двум динамическим рядам:
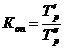7.9 или 
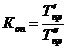, 7.10
где Т'р, Т''р, Т'рп, Т''пр – соответственно темпы роста и темпы прироста сравниваемых динамических рядов.
Задача 4. Грузооборот транспорта общего пользования в республике Беларусь (млн. т-км) составил:
| Железнодорожный | ||
| Автомобильный |
Определите коэффициент опережения роста автомобильного грузооборота.
Решение: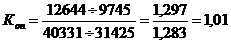 
,
т.е. грузооборот автомобильного транспорта за период 2000-2004 гг. опережал рост грузооборота железнодорожного транспорта в 1,01 раза.
Уровни и аналитические показатели динамики изменяются во времени. Поэтому для обобщающей характеристики всего ряда динамики в целом используются средние величины: средний уровень, средний абсолютный прирост, средний темп роста и прироста.
Средний уровень ряда динамики характеризует типичную величину абсолютных уровней. Он называется также средней хронологической, или временной средней и рассчитывается для разных рядов динамики по-разному.
В интервальных рядах с равными отрезками времени применяется средняя арифметическая простая:
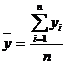, 7.11
где n – число уровней ряда.
Используя данные примера о динамике производства телевизоров, которые представляют собой интервальный динамический ряд с равными отрезками времени, рассчитаем среднегодовое производство телевизоров в Республике Беларусь за 2001-2004 гг.:
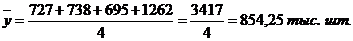
В интервальных рядах с неравными отрезками времени используется средняя арифметическая взвешенная:
В моментных рядах с равными промежутками между датами средний уровень рассчитывается по формуле:
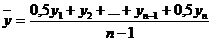, 7.12
где n -число дат,
(n-1) - число равных промежутков времени.
Задача 5. Остатки вкладов населения в банках в 1 квартале характеризуются следующими условными данными:
| на 1 января | на 1 февраля | на 1 марта | на 1 апреля | на 1 мая | на 1 июня | на 1 июля | |
| Остатки вкладов, млрд. руб. | 1416,3 | 1511,9 | 1611,6 | 1661,0 | 1740,5 | 1830,5 | 1928,0 |
Необходимо определить среднемесячный размер остатков вкладов населения в банках за 1 полугодие.
Решение: Приведенные данные представляют собой моментный динамический ряд с равноотстоящими уровнями. Следовательно, среднемесячный размер остатков вкладов населения в банках за 1 полугодие рассчитывается как:
Среднемесячный размер остатков вкладов населения в банках за 1 полугодие равен 1671,275 млрд. руб.
В моментных рядах с неравными промежутками между датами средний уровень рассчитывается двумя способами в зависимости от характера исходных данных. Если известны данные на начало изучаемого периода, а также изменения уровней ряда, то средний уровень рассчитывается по средней арифметической взвешенной:
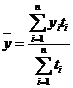, 7.13
где ti - продолжительность i -го отрезка времени.
Задача 6. В январе 2006 г. в списочном составе работников предприятия произошли следующие изменения, чел.:
состояло по списку на 1.01.2006 540
выбыло с 8.01 5
зачислено с 14.01 4
зачислено с 25.01 3
Необходимо определить среднедневную численность работников предприятия за январь.
Решение. Для определения среднедневной численности работников рассчитаем продолжительность (t) каждого календарного периода с постоянной численностью работающих и общее число человеко-дней:
| Календарные периоды января | Число работников (у) | Длина периода (t) | Число человеко-дней (уt) |
| 1-7 | |||
| 8-13 | |||
| 14-24 | |||
| 25-31 | |||
| Итого: | - |
Таким образом, среднесписочная численность работников в январе составит:
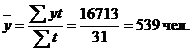
Если имеются данные на начало и конец периода, а также значения уровней динамического ряда на отдельные моменты времени внутри изучаемого периода, то средний уровень ряда рассчитывается по следующей формуле:
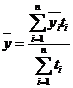, 7.14
где 
– промежуточная средняя, равная 
,
ti - продолжительность промежутка времени между соответствующими датами.
Задача 7. Изменение запасов готовой продукции по промышленным предприятиям характеризуется следующими условными данными:
| на 1 января | на 1 апреля | на 1 июня | на 1 ноября | на 1 января следующего года | |
| Запасы готовой продукции в текущих ценах, млрд. руб. | 1012,4 | 1320,7 | 1409,7 | 1320,5 | 1445,2 |
Определить среднемесячный размер запасов готовой продукции за год.
Решение: Данные о запасах готовой продукции по промышленным предприятиям представляют собой моментный ряд динамики с разноотстоящими уровнями, поэтому расчет среднемесячной величины запасов готовой продукции будет иметь следующий вид:
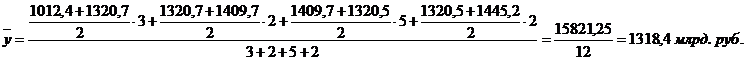
Таким образом, среднемесячный размер запасов готовой продукции за год составил 1318,4 млрд. руб.
Средний абсолютный прирост (или средняя абсолютная скорость роста) показывает, на сколько единиц в среднем увеличивался или уменьшался уровень динамического ряда за соответствующий период времени (за месяц, за квартал и т.д.) Он рассчитывается по средней арифметической простой из цепных абсолютных приростов за последовательные и равные по продолжительности периоды:
, 7.15
где n – число цепных абсолютных приростов.
Для нашего примера о производстве телевизоров значение данного показателя составит:
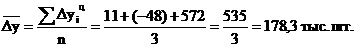
Таким образом, в среднем ежегодный абсолютный прирост производства телевизоров составлял 178,3 тыс. шт.
Средний темп роста рассчитывается по средней геометрической из цепных темпов роста, выраженных в коэффициентах:
а) с равными отрезками времени
, 7.16
где n – число цепных темпов роста;
б) с неравными отрезками времени:
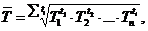, 7.17
где ti - продолжительность соответствующих отрезков времени.
В нашем примере средний темп роста производства телевизоров за 2001-2004 гг. составит:
Средний темп прироста показывает, на сколько процентов в среднем за единицу времени увеличивался или уменьшался уровень ряда динамики. Он рассчитывается как разность между средним темпом роста (
) и 100%, если выражен в процентах, а если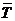 
выражен в коэффициентах, то 
.
Так, в среднем ежегодно производство телевизоров в Республике Беларусь увеличивалось на 14,8% (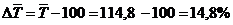
).
Важной задачей анализа рядов динамики является выявление и изучение закономерностей изменения уровней, общей тенденции развития (тренда) исследуемого явления. Под общей тенденцией динамики понимается тенденция к росту, к стабильности или к снижению уровня изучаемого явления. Наличие колебаний уровней в ряду динамики затрудняет выявление типа тенденции динамики. Чтобы устранить влияние случайных причин и сгладить колеблемость уровней динамического ряда, его обрабатывают различными статистическими методами. Наиболее распространенными способами обработки динамических рядов являются: укрупнение интервалов, сглаживание по способу скользящей (подвижной) средней, аналитическое выравнивание ряда динамики (использование метода наименьших квадратов).
Одним из наиболее простых приемов является укрупнение интервалов времени, к которым относятся уровни динамического ряда (месячные данные в квартальные или годовые, квартальные в годовые и т.п.). Вновь образованный ряд может состоять либо из абсолютных суммарных показателей, полученных за более длительные промежутки времени, либо из средних уровней по этим укрупненным интервалам. В таком ряду за счет взаимопогашения случайных отклонений более четко проявляется общая тенденция изменения уровней.
Задача 8. Имеются следующие фактические данные о перевозке грузов железнодорожным транспортом в Республике Беларусь по месяцам 2004 г., млн. тонн:
| январь | 7,8 | июль | 9,3 |
| февраль | 8,2 | август | 9,9 |
| март | 9,5 | сентябрь | 9,5 |
| апрель | 9,1 | октябрь | 9,9 |
| май | 9,5 | ноябрь | 9,7 |
| июнь | 9,0 | декабрь | 9,8 |
Для выявления общей тенденции роста объемов перевозок грузов железнодорожным транспортом необходимо произвести укрупнение интервалов.
Решение: Для этой цели исходные (месячные) данные объединим в квартальные и получим показатели объема перевозок грузов железнодорожным транспортом по кварталам 2004 г., млн. тонн:
| І | ІІ | ІІІ | ІV |
| 25,5 | 27,6 | 28,7 | 29,4 |
В результате укрупнения интервалов общая тенденция роста объема перевозок железнодорожным транспортом выступает отчетливо:
25,5 < 27,6 < 28,7 < 29,4.
По полученным квартальным показателям можно рассчитать средний объем перевозок грузов железнодорожным транспортом за каждый квартал, млн. тонн:
| І | ІІ | ІІІ | ІV |
| 25,5:3=8,5 | 27,6:3=9,2 | 28,7:3=9,6 | 29,4:3=9,8 |
Полученные средние подтверждают вывод о наличии тенденции к росту к концу года объема перевозок грузов железнодорожным транспортом в 2004 г.:
8,5 < 9,2 < 9,6 < 9,8.
Другим приемом выявления общей тенденции является метод скользящей (подвижной) средней. Суть этого метода заключается в том, что исходный ряд динамики заменяется рядом средних уровней, рассчитанных по укрупненным периодам равной продолжительности. Каждая последующая средняя получается после смещения начала периода на единицу времени вперед. Первый интервал будет включать уровни y1, y2, …, yk; второй – уровни y2, y3, …, yk, yk+1 и т.д. Таким образом, при использовании данного метода происходит как бы скольжение по ряду динамики от его начала до конца, при этом первый уровень каждый раз отбрасывается и добавляется следующий, а затем фактические уровни заменяются средними.
Полученные средние относятся к середине соответствующего периода скольжения, если он состоит из нечетного числа интервалов времени: трех, пяти, семи и т.д.
Если же сглаживание производится по четному числу уровней: двум, четырем, шести и т.д., то полученные скользящие средние могут быть отнесены только к середине между двумя уровнями, находящимися в центре интервала скольжения. Для ликвидации такого сдвига производится дополнительная процедура – центрирование. При этом рассчитывают средние арифметические простые из каждых двух уже рассчитанных соседних скользящих средних и относят их соответственно ко второму из центральных уровней в каждом укрупненном интервале.
Рассмотрим применение метода скользящей средней на основании данных предыдущей задачи. Определим среднемесячный объем перевозок грузов железнодорожным транспортом, используя четырехчленную скользящую среднюю. Применительно к исходным данным получим десять средних, млн. тонн:
первая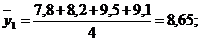 
вторая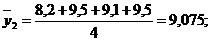 
третья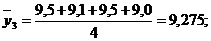 
……………………………………….
десятая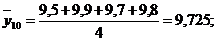 
.
Особенность сглаживания по четному числу уровней состоит в том, что каждая из исчисленных четырехчленных средних относится к соответствующим промежуткам между двумя смежными месяцами. Так, первая средняя (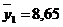
) относится к промежутку между февралем и мартом 2004 г., вторая средняя (
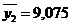) – к промежутку между мартом и апрелем 2004 г. и т.д.
Для получения сглаженных уровней соответствующих месяцев необходимо произвести центрирование расчетных средних.
Так, для определения сглаженного среднего уровня за март 2004 г. произведем центрирование первой средней 
и второй средней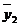 
:
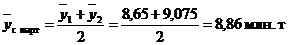. 7.18
Для определения сглаженного среднего уровня за апрель 2004 г. произведем центрирование второй средней 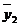и третьей средней 
:
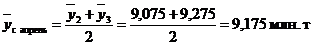и т.д. 7.19
Ход расчета необходимых данных для получения средних (теоретических) уровней представим в таблице сглаживания ряда динамики по четырехчленной переменной (скользящей) средней:
Таблица 7.1
| Месяц 2004 г. | Исходные уровни (уi) | Средняя из суммы четырех уровней ряда | Сглаженный средний уровень
(с центрированием,  )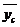
|
| Январь | 7,8 | - | |
| Февраль | 8,2 | - | |
| 34,6/4=8,65 | |||
| Март | 9,5 | 8,86 | |
| 36,3/4=9,075 | |||
| Апрель | 9,1 | 9,175 | |
| 37,1/4=9,275 | |||
| Май | 9,5 | 9,25 | |
| 36,9/4=9,225 | |||
| Июнь | 9,0 | 9,325 | |
| 37,7/4=9,425 | |||
| Июль | 9,3 | 9,425 | |
| 37,7/4=9,425 | |||
| Август | 9,9 | 9,53 | |
| 38,6/4=9,65 | |||
| Сентябрь | 9,5 | 9,7 | |
| 39,0/4=9,75 | |||
| Октябрь | 9,9 | 9,738 | |
| 38,9/4=9,725 | |||
| Ноябрь | 9,7 | - | |
| Декабрь | 9,8 | - |
Таким образом, сглаженные уровни среднего уровня объема перевозок грузов железнодорожным транспортом четко отражают тенденцию к росту данного показателя.
Более совершенным способом выявления основной тенденции изменений всех уровней динамического ряда является аналитическое выравнивание ряда динамики (определение тренда).
Сущность этого способа заключается в нахождении такой аналитической прямой или кривой, ординаты точек которой были бы наиболее близкими к уровням исследуемого динамического ряда, т.е. наилучшим образом отражали бы характер изменения изучаемого явления во времени.
Основным содержанием метода аналитического выравнивания в динамических рядах является то, что закономерно изменяющийся уровень изучаемого экономического явления рассчитывается как функция времени (тренд):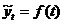 
. Уравнение этой аналитической кривой называется уравнением основной тенденции или уравнением тренда. Наиболее часто для аналитического выравнивания используются следующие виды трендовых моделей:
Основные виды трендовых моделей
| №п/п | Название функции | Описание функции |
| 1. | Линейная |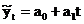 
|
| 2. | Парабола второго порядка | 
|
| 3. | Кубическая парабола |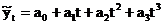 
|
| 4. | Показательная |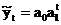 
|
| 5. | Экспоненциальная | 
|
| 6. | Модифицированная экспонента |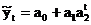 
|
| 7. | Гиперболическая |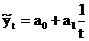 
|
Выбор конкретного вида прямой или кривой осуществляется на основе всестороннего анализа закономерностей и характера развития явлений и фактических показателей, представленных в динамическом ряду.
Параметры аналитического уравнения выбранного вида кривой находят, используя способ наименьших квадратов. При этом предполагается, что сумма квадратов отклонений фактических уровней (yi)от выравненных (
), т.е. расположенных на искомой линии, должна быть минимальной:
7.20
Рассмотрим технику выравнивания ряда динамики по уравнению тренда прямой, т.е. по линейной функции:
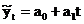, 7.21
где t – условное обозначение времени,
a0, a1 – параметры искомой прямой.
Выравнивание по прямой применяется в тех случаях, когда характер движения изучаемого явления ближе всего к прямолинейному. При этом наблюдаются примерно равные постоянные цепные абсолютные приросты.
Параметры а0 и а1 находятся путем решения следующей системы нормальных уравнений:
7.22
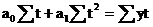7.23
где y – фактические уровни ряда динамики;
n – число уровней ряда;
t – соответствующая нумерация фактора времени.
Эта система уравнений значительно упрощается, если значения времени подобрать так, чтобы их сумма равнялась нулю. Тогда:
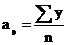7.24; 
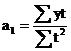7.25
Если число уровней в ряду динамики четное, то условные обозначения времени t принимаются следующие:
| Годы | ||||||||
| t | -7 | -5 | -3 | -1 | +1 | +3 | +5 | +7 |
Если число уровней в ряду динамики нечетное, то отсчет ведется от середины, взятой за ноль:
| Годы | |||||||
| t | -3 | -2 | -1 | +1 | +2 | +3 |
Полученное в результате произведенных расчетов аналитическое уравнение представляет собой математическую модель развития изучаемого явления и выражает статистическую закономерность, проявляющуюся в анализируемом ряду динамики.
Рассмотрим применение метода аналитического выравнивания по прямой для выражения общей тенденции на примере данных о перевозке грузов железнодорожным транспортом в Республике Беларусь по месяцам 2004 г., приведенных в предыдущей задаче.
Применительно к исходным данным, в которых число исходных (эмпирических) уровней ряда – четное (n =12), условные обозначения времени будут выглядеть следующим образом:
| январь | февраль | март | апрель | май | июнь | июль | август | сентябрь | октябрь | ноябрь | декабрь |
| -11 | -9 | -7 | -5 | -3 | -1 | +1 | +3 | +5 | +7 | +9 | +11 |
Расчет необходимых значений произведем в таблице:
| Месяц 2004 г. | Эмпирические уровни ряда (уi) | Условные обозначения времени (t) | t2 | у t | у t =9,267+0,073 |
| январь | 7,8 | -11 | -85,8 | 8,47 | |
| февраль | 8,2 | -9 | -73,8 | 7,55 | |
| март | 9,5 | -7 | -66,5 | 8,58 | |
| апрель | 9,1 | -5 | -45,5 | 8,90 | |
| май | 9,5 | -3 | -28,5 | 9,05 | |
| июнь | 9,0 | -1 | -9,0 | 9,19 | |
| июль | 9,3 | +1 | 9,3 | 9,34 | |
| август | 9,9 | +3 | 29,7 | 9,49 | |
| сентябрь | 9,5 | +5 | 47,5 | 9,63 | |
| октябрь | 9,9 | +7 | 69,3 | 9,78 | |
| ноябрь | 9,7 | +9 | 87,3 | 9,93 | |
| декабрь | 9,8 | +11 | 107,8 | 10,07 | |
| Итого: | 111,2 | 41,8 | 109,96 |
По итоговым данным определяем параметры уравнения:
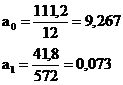
Выравненные значения объема перевозок грузов железнодорожным транспортом в Республике Беларуси в 2004 г. свидетельствуют о тенденции к росту данного показателя во времени.
При изучении месячных или квартальных уровней рядов динамики часто обнаруживаются постоянно повторяющиеся их колебания, существенно не изменяющиеся за длительный период времени. Такие изменения уровней ряда называют сезонными колебаниями. Для их выявления анализируются месячные или квартальные уровни динамического ряда за ряд лет. Характеристику сезонных колебаний производят с помощью индексов сезонности (IS). Способ определения индексов сезонности зависит от характера общей тенденции ряда динамики.
Если ряд динамики не содержит ярко выраженной тенденции в развитии, то изучение сезонности производят с помощью метода постоянной средней. Расчет индексов сезонности в таких рядах осуществляется по следующей формуле:
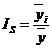, 7.26
где 
– осредненные эмп