1. Лишние цифры в целых числах заменяются нулями, а в десятичных дробях отбрасываются. Если десятичная дробь в числовом значении результата измерения оканчивается нулями, то нули отбрасываются только до того разряда, который соответствует разряду погрешности.
Пример 4.
Х=2,0700, Δ=0,001 => Х≈2,070.
2. Если цифра старшего из отбрасываемых разрядов меньше 5, то остающиеся цифры числа не изменяют.
Пример 5.
Число 253435 округляют до четырех значащих цифр. Получают 253400.
Число 235,435 ≈ 235,4
3. Если цифра старшего из отбрасываемых разрядов больше или равна 5, но за ней следуют отличные от нуля цифры, то последнюю оставляемую цифру увеличивают на единицу.
Пример 6.
18598 ≈ 18600 (до трех значащих цифр),
152,56 ≈ 153 (до трех значащих цифр).
4. Если отбрасываемая цифра равна 5, а следующие за ней цифры неизвестны или равны нулю, то последнюю сохраняемую цифру не изменяют если она четная, и увеличивают, если она нечетная.
Пример 7.
При сохранении двух значащих цифр
22,5 округляют до 22,
23,5 округляют до 24.
3.3. Систематические погрешности. Обнаружение и исключение.
Источниками систематических составляющих погрешности измерения могут быть все его компоненты: метод измерения, средства измерений и экспериментатор.
Постоянные инструментальные систематические погрешности обычно выявляют посредством поверки средства измерений.
Поверкой называют определение метрологическим органом погрешностей средства измерений и установление пригодности средства измерений к применению. Обнаруженные путем поверки систематические погрешности исключаются из результата измерения путем введения поправки.
Пример 8.
При измерении напряжения в сети показания вольтметра 225 В. В свидетельстве о поверке указано, что на этой отметке шкалы систематическая погрешность вольтметра равна +3 В. С учетом поправки напряжение в сети равно 225-3=222 В.
Для обнаружения изменяющейся систематической погрешности рекомендуется построить график, на котором нанесены результаты наблюдений в той последовательности, в какой они были получены. Простейшим случаем является погрешность, прогрессирующая по линейному закону, например, пропорционально времени.
х
х2
х1
х0
 |
t1 t2 t
Рис 3.2. Линейное изменение систематической погрешности.
Такие погрешности могут быть оценены и исключены следующим образом. Если известно, что при измерении постоянной величины х0 систематическая погрешность изменяется линейно во времени, т.е.
х=х0 +Сt (где С=const),
То для ее исключения достаточно сделать 2 наблюдения х1 и х2 с фиксацией времени t1 и t2, тогда искомое значение величины будет
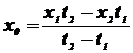. (3.7.)
Однако, далеко не всегда систематическая погрешность изменяется по линейному закону. В этом случае для контроля систематической погрешности применяется метод симметричных наблюдений.
Выполняют несколько наблюдений через равные промежутки времени. Вычисляют средние арифметические симметрично расположенных отсчетов
.
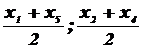Теоретически, при линейной зависимости погрешности от времени, эти средние арифметические должны быть равны. Убедившись, что погрешность изменяется по линейному закону, находят результат по вышеприведенной формуле.
х
х5
х4
х3
х2
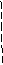
х1
х0 
t1 t2 t3 t4 t5 t
Рис.3.3. Иллюстрация метода симметричных наблюдений
Систематические составляющие, обусловленные несовершенством методов измерения, ограниченной точностью расчетных формул, положенных в основу измерений, влиянием средств измерений на объект, свойства которого измеряются, относятся к методическим погрешностям. Единых рекомендаций по обнаружению и оцениванию методических составляющих систематической погрешности нет. Задача решается в каждом конкретном случае индивидуально, на основе анализа примененного метода измерений, результаты которого часто зависят от квалификации и опыта экспериментатора.
Пример 9.
Ux
Rv
Ri
Оценить систематическую погрешность измерения напряжения Ux источника, обусловленную наличием внутреннего сопротивления вольтметра. Внутреннее сопротивление источника напряжения Ri =50 Oм; сопротивление вольтметра Rv =5 кОм; показание вольтметра Uизм =12,2 В.
Решение.
Здесь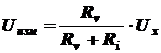 
и относительная систематическая погрешность 
.
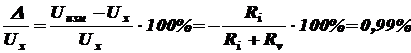Это достаточно ощутимая погрешность и ее следует учесть введением поправки. Поправка Ñ равна погрешности, взятой с обратным знаком.
Ñ=0,99·10-2·12,2=+0,12 В.
Ux =12,2+0,12=12,32 В.
Полученная оценка имеет погрешность из-за погрешностей в определении и, а также из-за инструментальной погрешности вольтметра. Эта погрешностью при введении поправки не исключается и называется неисключенным остатком систематической погрешности.
Личные систематические погрешности связаны с индивидуальными особенностями наблюдателя. Для уменьшения этого вида погрешностей надо точно соблюдать правила эксплуатации средств измерений и иметь навыки работы с измерительной техникой.
3.4. Случайные погрешности. Вероятностное описание результатов и погрешностей
Когда при проведении в одинаковых условиях повторных измерений одной и той же постоянной величины получаем результаты, отличающиеся друг от друга, это свидетельствует о наличии в них случайных погрешностей. Эта погрешность возникает вследствие одновременного воздействия на результат многих случайных возмущений и сама является случайной величиной. В этом случае предсказать результат отдельного измерения и исправить его введением поправки невозможно. Можно лишь с определенной долей уверенности утверждать, что истинное значение измеряемой величины находится в пределах разброса результатов наблюдений от хmin до хmax, где хmin и хmax – соответственно нижняя и верхняя граница разброса.
Для установления вероятностных (статистических) закономерностей появления случайных погрешностей и количественной оценки результата измерений и его случайной погрешности используются методы теории вероятностей и математической статистики.
Для характеристики свойств случайной величины в теории вероятностей используют понятие закона распределения вероятностей случайной величины. Различают две формы описания закона распределения: интегральную и дифференциальную. В метрологии преимущественно используется дифференциальная форма – закон распределения плотности вероятностей случайной величины.
Рассмотрим формирование дифференциального закона.
1. Проведем n измерений одной величины Х.
2. Получим группу наблюдений х1; х2,…,хn.
3. Расположим результаты в порядке возрастания от хmin до хmax.
4. Найдем размах ряда L=хmax - хmin.
5. Разделим размах ряда на k равных интервалов ∆l=L/k.
6. Подсчитаем количество наблюдений nk, попадающих в каждый интервал.
7. Изобразим полученные результаты графически (по оси абсцисс – значения физической величины с границами интервалов; по оси ординат – относительная частота попаданий nk/n.
8. Достроив по полученным точкам соответствующие прямоугольники получим гистограмму, дающую представление о плотности распределения результатов наблюдений в данном опыте.
Пример 10. N=50 измерений.
| N интервала | |||||
| nk | |||||
| nk/n | 0,1 | 0,2 | 0,36 | 0,22 | 0,12 |
 |
 |
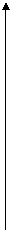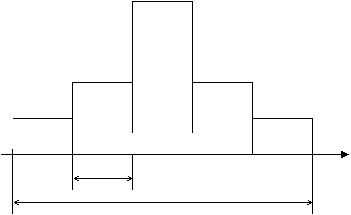Если распределение случайной величины статистически устойчиво, то можно ожидать, что при повторных сериях наблюдений той же величины в тех же условиях, относительные частоты попаданий в каждый интервал будут близки к первоначальным. Следовательно, по гистограмме можно предсказывать распределение результатов измерений по интервалам.
При бесконечном увеличении числа наблюдений и бесконечном уменьшении ширины интервалов, ступенчатая кривая, огибающая гистограмму, перейдет в плавную кривую f(x), которая называется кривой плотности распределения вероятностей случайной величины, а уравнение ее описывающие дифференциальным законом распределения. Кривая плотности распределения вероятностей всегда неотрицательна и подчинена условию нормирования в виде:
Если известен закон распределения случайной величины f(x), то вероятность Р ее попадания в интервал от х1 до х2
Для описания частных свойств случайной величины используют числовые характеристики распределений. В качестве числовых характеристик выступают моменты случайных величин: начальные и центральные. Все они представляют собой некоторые средние значения. Причем, если усредняются величины, отсчитываемые от начала координат, моменты называют начальными, а если от центра закона распределения, то центральными.
Начальный момент k-го порядка определяется формулой
.
Из начальных моментов наибольший интерес представляет математическое ожидание случайной величины (k=1)
.
Центральные моменты k-го порядка рассчитываются по формулам%
.
Из центральных моментов особенно важную роль играет второй момент (k=2), дисперсия случайной величины D
.
Дисперсия случайной величины характеризует рассеяние отдельных ее значений. Дисперсия имеет размерность квадрата случайной величины и выражает как бы мощность рассеяния относительно постоянной составляющей. Однако чаще пользуются положительным корнем квадратным из дисперсии – средним квадратическим отклонением (СКО), которое имеет размерность самой случайной величины.
Способы нахождения оценок результата измерения зависят и от имеющихся соглашений по этому вопросу, регламентируемых в рамках законодательной метрологии. В стандарте на методы обработки результатов прямых измерений с многократными наблюдениями указывается, что приведенные в нем методы обработки установлены для результатов наблюдений, принадлежащих нормальному распределению.
Нормальное распределение плотности вероятности характерно тем, что такое распределение имеет сумма бесконечно большого числа бесконечно малых случайных возмущений с любыми распределениями. Применительно к измерениям это означает, что нормальное распределение случайных погрешностей возникает тогда, когда на результат измерения действует множество случайных возмущений, ни одно из которых не является преобладающим.
Кривые нормального распределения выглядят следующим образои.
Рис.3.4. Кривые нормального распределения.
В аналитической форме нормальный закон распределения выражается формулой
Где х – случайная величина;
mx - математическое ожидание случайной величины;
δ – СКО.
Перенеся начало координат в mx и откладывая по оси абсцисс погрешность Δх=х-mx, получим кривую нормального распределения погрешностей
.
Для группы из n наблюдений, распределенных по нормальному закону
.Обратим внимание на некоторые свойства нормального распределения.
1. Кривая нормального распределения погрешностей симметрична относительно начала координат. Это означает, что погрешности, одинаковые по величине, но противоположные по знаку, имеют одинаковую плотность вероятности, т.е. при большом числе наблюдений встречаются одинаково часто. Математическое ожидание случайной погрешности равно нулю.
2. Из характера кривой следует, что при нормальном законе распределения малые погрешности будут встречаться чаще, чем большие. Вероятность появления погрешностей в интервале от 0 до Δх1, характеризуемая площадью S1 больше, чем вероятность появления погрешностей в интервале от Δх2 до Δх3 (площадь S2).
3. Сравнивая кривые нормального распределения с различными СКО (σ1>σ2>σ3), можно видеть, что чем меньше СКО, тем меньше рассеяние результатов наблюдений и тем больше вероятность того, что большинство случайных погрешностей в них будет мало.
Более подробно с методами оценки систематических и случайных погрешностей измерений познакомимся позднее в теме “Обработка результатов измерений”.