Цели урока:
1) учить объединять предметы в группы по сходным признакам и выделять из группы отдельные предметы;
2) закреплять умения сравнивать численности множеств, располагать предметы в порядке увеличения (уменьшения), вести количественный и порядковый счет предметов в пределах 10;
3) совершенствовать знания о свойствах и взаимном расположении предметов.
ХОД УРОКА
1. Организационный момент.
2. Устные упражнения и практическая работа.
1) Счет в пределах 10 (прямой и обратный) с передачей предмета.
2) Задание на внимание.
— Если услышите название цветка — поднимите правую руку, животного — левую. (Заяц, тигр, ромашка, слон, роза, медведь, собака, астра, василек.)
3) Геометрическое лото. Работа в парах.
— Выберите любую красную фигуру из геометрического лото. Как она называется?
— Составим узор. Положите на стол выбранную фигуру. Справа от нее положите такую фигуру из геометрического лото, у которой был бы тот же цвет, но другая форма. Потом положите еще одну фигуру, чтобы изменился цвет, а форма осталась прежней. Затем измените форму. И наконец, измените форму и цвет.
— Сколько всего фигур в этом узоре? Сколько в нем фигур одного цвета? Одной формы? Могли ли быть в этом узоре три красные фигуры?
3. Изучение нового.
Группировка предметов по общим признакам.
— Отгадайте, о каком времени года эта загадка:
| Прошла по лугам, по полям, по лесам, Припасы она заготовила нам. Упрятала их в погреба, в закрома. Сказала: «За мною нагрянет зима». (Осень.) |
— Сколько осенних месяцев? (Три.)
— Назовите их по порядку. (Сентябрь, октябрь, ноябрь.)
— Осенью созревает богатый урожай овощей, фруктов, ягод, грибов, цветов. (На доске учитель прикрепляет изображения этих предметов.)
— Поможем Зайчику и Белочке разобрать урожай. Что будет запасать на зиму Зайчик? (Овощи.)
(Вызванный к доске ученик отбирает овощи и прикрепляет их отдельно.)
— А Белочка? (Грибы.)
(Другой ученик отбирает картинки с грибами и прикрепляет их отдельно.)
— На какие группы можно разбить оставшиеся картинки? (Фрукты, ягоды, цветы.)
— Все эти группы предметов в математике называются множествами. Например, множество овощей (учитель показывает эту группу картинок, обводя ее мелом плавной линией), множество грибов и т. д.
— Какие еще множества мы выделили? Покажите.
— Каждый предмет в отдельности — элемент множества. Например, огурец — элемент множества овощей. Мухомор — элемент множества грибов.
— Назовите элементы множества фруктов. Элементом какого множества является василек?
4. Работа по учебнику.
Выполнение заданий учебника на с. 28—29.
1) Подбор обобщающего слова для множества предметов. Счет и выделение элементов множества.
— Рассмотрите каждое множество предметов. Придумайте ему название. (Грибы, бабочки, конфеты.) Сколько элементов в множестве бабочек? В множестве конфет? Элементом какого множества является рыжик? Леденцы?
2) Второе задание на с. 28 выполняется аналогично. Беседа по усмотрению учителя.
3) При выполнении первого задания на с. 29 учащиеся должны познакомиться с понятиями четырехугольника и пятиугольника.
— На какие три множества можно разбить фигуры на рисунке? (Треугольники, четырехугольники, пятиугольники.) По какому признаку выделяли эти множества? (По форме.)
— Разбейте эти фигуры на группы по цвету. Сколько множеств получилось? (Четыре: синие, оранжевые, зеленые и розовые фигуры.)
5. Физкультминутка.
Поднимает руки класс — это «раз»,
Повернулась голова — это «два»,
Руки вниз, вперед смотри — это «три»,
Руки в стороны пошире развернули на «четыре»,
С силой их к плечам прижать — это «пять».
Всем ребятам тихо сесть — это «шесть».
6. Повторение. (Продолжение работы с учебником.)
1) Задание 2, с. 29. Чтобы узнать, каков порядок расположения бейсболок хотел нарисовать художник, учащиеся должны соотнести цветную схему с размерами бейсболок. Объяснения при этом могут быть такими: «Первой стоит синяя бейсболка, она самая большая. Потом идет зеленая, она поменьше. Дальше — черная бейсболка, она еще меньше. И последняя самая маленькая — красная бейсболка. Порядок от большего к меньшему называется уменьшением.
Пользуясь схемой, учащиеся далее отвечают на другие вопросы учебника.
2) Задание 3, с. 29, требует знания порядка чисел в натуральном ряду. Так, рассуждения учащихся при заполнении схемы слева могут быть следующими: «Нам нужно заполнить точками два пустых кружка. В одном кружке должно быть точек больше, чем три. Пусть это четыре точки. Тогда в следующем кружке должно быть точек больше, чем четыре. Допустим, это пять точек. Проверяем: 5 точек больше, чем 2 точки. Выполнено верно». Разумеется, здесь могли быть и другие ответы. Например, четыре и шесть, пять и восемь и т. п.
7. Физкультминутка.
| Раз, два, три, четыре, пять! Будем пальчики считать — Крепкие, дружные, Все такие нужные. На другой руке опять: Раз, два, три, четыре, пять! Пальчики быстрые, Хоть не очень... чистые. |
8. Работа в тетради.
Выполнение рисунка по образцу в учебнике.
9. Итог урока.
— Что нового вы узнали на уроке?
— Какие задания вы выполняли? Какие вам понравились?
— К следующему уроку придумайте множества предметов и назовите элементы этих множеств.
Раздел 2.
МНОЖЕСТВА И ДЕЙСТВИЯ НАД НИМИ
Разнообразие заданий на группировку предметов по заданному признаку и выделение из множества его части, также рассматриваемые в подготовительный период, обеспечивают необходимую подготовку детей к усвоению в дальнейшем смысла действий сложения и вычитания. Учитывая большое образовательное и развивающее значение заданий на классификацию и сериацию предметов, в учебнике эти упражнения проходят сквозной линией, усложняясь по мере продвижения по курсу от темы к теме.
Особое место в этом разделе занимает изучение геометрического материала. Сразу заметим, что геометрический материал, вообще говоря, рассредоточен по всему учебнику, но именно на этом этапе будут проводиться первые уроки, специально посвященные ознакомлению с основными геометрическими фигурами (точки и линии, прямая и кривая линии) и отношениями «вне», «внутри», «между».
Рассматриваемые геометрические фигуры (треугольник, квадрат и круг) выступают в этот период лишь в качестве дидактического материала.
Как известно, успешное формирование такого абстрактного понятия, как «геометрическая фигура» (всякое множество точек), во многом зависит от многообразия представлений, накопленных учащимися. Поэтому главными источниками этих знаний являются наглядно-предметная деятельность детей и речь, сопровождающая эту деятельность. Так, наблюдая окружающие их предметы, их части, контуры или модели этих предметов и их частей, дети учатся находить и показывать предметы, похожие на изучаемые геометрические фигуры. В частности, дети учатся «видеть» знакомые фигуры на точечном множестве, разбивая его на части по заданному признаку. Для развития геометрической зоркости малышей, их воображения и фантазии полезно предлагать задания творческого плана на «домысливание» и опредмечивание схематических рисунков.
— Посмотрите на рисунок. Что напоминают вам эти линии? (На доске — пейзаж, элементы которого представляют собой замкнутые и незамкнутые кривые линии, многоугольники.)

Из точки А по стеклу течет капля дождя. Подумайте, может ли она оставить такой след. (На доске — варианты кривых линий, проведенных из точки.)

Изучение отношений «вне», «внутри» и «между» проводится на наглядно-деятельностной основе с использованием предметных множеств, картинок или практических действий.
Например, учитель просит нескольких учащихся встать в круг и водить хоровод. Далее по просьбе учителя один ученик становится внутри круга, а другой — вне его. При этом учитель спрашивает:
— Кто водит хоровод? (Дети называют имена учеников.)
— На какую фигуру похоже кольцо хоровода? (Круг.) (Учитель рисует на доске круг.)
— Кто стоит внутри круга? (Имя ученика, например Вася.)
Учитель на доске ставит точку внутри круга и рядом с ней пишет заглавную букву имени этого ученика, букву В.
— Мальчика Васю на чертеже обозначим точкой В.
— Кто не попал в круг, кто за кругом? (Имя ученика, например Аня.)
— За кругом или по-другому, вне круга, стоит Аня. Учитель на доске ставит точку вне круга, а рядом с ней заглавную букву А.
 — Девочку Аню тоже обозначим точкой, поставим ее вне круга, а рядом напишем букву А. (На доске появляется рисунок.)
— Девочку Аню тоже обозначим точкой, поставим ее вне круга, а рядом напишем букву А. (На доске появляется рисунок.)
— Как вы думаете, почему я так назвала эту точку? (Дети отвечают.)
— Назовите точку внутри круга (вне круга).
— Как бы вы отметили на рисунке ребят, водивших хоровод? (Желательно, чтобы дети предложили отметить их точками на линии круга (окружности).
— Какие имена мы дадим этим точкам?
— Кто стоит между Борей и Леной? между Светой и Катей?
По просьбе учителя к доске выходят ученики и последовательно отмечают точки на окружности, дают им имена. Например: С, Б, К, Л, Н.
 — Сколько точек мы отметим на линии круга?
— Сколько точек мы отметим на линии круга?
— Какая точка расположена между Б и Л? между К и Н?
В итоге прежний рисунок преобразуется.
По существу, это первый опыт создания геометрической модели реальной жизненной ситуации. В дальнейшем эти умения будут закреплены и использованы при работе с чертежами и составлении краткой записи к задачам.
Особое место в этой системе занимают задания-схемы на сравнение численностей множеств, которые по существу можно рассматривать как иную форму записи двойных неравенств с переменной. Но если обычные неравенства являются наиболее сложными задачами школьной математики, а их решение вызывает у учащихся порою непреодолимые затруднения, то в данной постановке эти задания первоклассники выполняют весьма легко.
Но мы бы не ставили фактор легкости как аргумент для включения этих заданий в курс обучения, если бы не большое развивающее значение этих упражнений. И здесь не только пропедевтика алгебры, что само по себе важно. Это, прежде всего, упражнения, на которых дети хорошо усваивают порядок следования чисел в натуральном ряду и развивают логику рассуждений.
Рассмотрим методику работы с одним из первых заданий этого типа.
С. 25. Расставь точки в пустые кружки так, чтобы соблюдалось правило: стрелка направлена от кружка с бóльшим количеством точек к кружку с меньшим количеством точек.
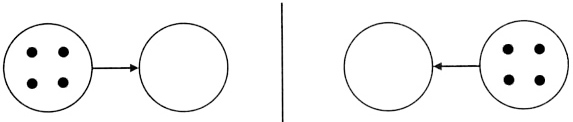
Учитель замечает, что поскольку стрелки на второй схеме проведены справа налево, то удобно рассматривать их в этом направлении.
— Сколько точек в правом кружке? (Четыре.) Что означает стрелка, проведенная от кружка справа к пустому кружку? (В кружке справа точек больше, чем в пустом кружке.) Что тогда можно сказать про количество точек в пустом кружке? (Их должно быть меньше четырех.)
В дальнейшем эти задания усложняются и приобретают более творческий характер за счет открытой постановки условий.
Раздел 3.
ЧИСЛА ОТ 1 ДО 10. ЧИСЛО 0
Заметим, что основное содержание этого раздела имеет целью сформировать знания учащихся о способах образования натуральных чисел путем присчитывания и отсчитывания единицы, познакомить учащихся с цифрами от 0 до 9, научить сравнивать числа, знать их порядок и состав.
Фактически в результате изучения предыдущего материала у учащихся уже сформирована нужная мотивация для ввода чисел и цифр.
Напомним, что нумерация чисел первого десятка выделяется в особый концентр, так как наша система счисления десятичная. В основе устной и письменной нумерации лежат названия и обозначения первых девяти чисел натурального ряда и числа 0. Каждая цифра на письме имеет особый знак, а в устной речи имеется особое слово, обозначающее данное число. Счет в пределах 10 — основа овладения счетом вообще, так как десятки, сотни, тысячи и др. считаются так же, как и простые единицы.
Главной задачей учителя в период изучения этого раздела является ознакомление детей с каждым из первых 9 чисел натурального ряда и числом 0, а также с соответствующими цифрами, их названиями, количественным и порядковым значением.
Согласно данному учебнику, особенность этих уроков состоит еще и в том, что объяснительный текст строится на основе рассмотрения одной и той же жизненно-практической ситуации, которая дается в развитии: у курочки-наседки из десяти яиц по одному вылупляются цыплята. Такой подход дает возможность детям осознать закон сохранения количества: если где-то прибавляется единица, то это значит, что где-то единица убывает.
С числом 1 дети знакомятся сопоставлением понятий «много» и «один». После рассмотрения примеров различных множеств предметов, среди которых есть одноэлементные множества, говорят, что слово «один» записывается цифрой 1.
Со всеми другими числами рекомендуется знакомить детей в следующем порядке.
1) Повторение образования каждого изученного (предыдущего) числа. Это объясняется тем, что принцип построения натурального ряда начинается с получения следующего числа путем прибавления единицы к предыдущему числу. Например, при ознакомлении с числом 4 сначала повторяется образование предыдущих чисел. Для этого учитель ставит последовательно на наборное полотно изображения цыплят (сначала один, потом еще один и т. д. до четырех). Задавая вопросы: «Сколько цыплят?» и «Как получили число два (три, четыре)?», учитель попутно в столбик записывает: 1, 1 + 1 = 2, 2 + 1 = 3, 3 + 1 = 4.
2) Показывается образование нового числа и указывается его название. Например, добавив к трем цыплятам еще одного, учащиеся выясняют, что получилось 4 и 4 — это 3 + 1.
3) Подбор к числу эквивалентных множеств. Например, по заданию учителя учащиеся называют предметы, которые встречаются по 4: 4 ножки у стула, 4 колеса у машины, 4 ноги у собаки и т. д. Можно также предложить задание на зарисовку.
— Нарисуйте четыре кружка на одной строке. Нарисуйте на второй строке четыре елочки.
Учитель показывает карточку с цифрой 4 и говорит: «Обведите в тетради столько же клеточек».
4) Счет в пределах данного числа, использование, по возможности, соответствующего геометрического материала. Например, на наборном полотне выставляются различные четырехугольники.
— Посчитайте, сколько сторон (углов)? Почему эти фигуры называются четырехугольниками?
5) Использование числовых фигур, рассмотрение состава числа: 4 — это 3 и 1; 4 — это 2 и 2.

6) Сравнение данного числа с предыдущими:
— В магазине на полке стоят игрушки. Сколько зайчиков? (3.) Сколько кукол? (4.) Каких игрушек больше? (Кукол больше, чем зайчиков.) Пришла в магазин девочка и купила одну куклу. Кукол стало больше или меньше? (Меньше.) Сколько стало кукол? (3 куклы.) Как узнали? (4 – 1 = 3.) Что можно сказать о числе кукол и зайчиков? (Их стало поровну.)
Дети должны усвоить к концу изучения темы два способа образования чисел натурального ряда: путем прибавления к предыдущему числу единицы или вычитанием единицы из последующего числа.
7) Знакомство с письмом цифры. Сначала учитель показывает образец написания цифры на доске. Затем дети разглядывают аналогичный образец в учебнике. Повторяют движения «в воздухе» и пишут в тетради несколько строчек. В воспитательных целях полезно всему классу демонстрировать лучшее написание.
Заметим, что при знакомстве с каждым из чисел первого десятка необходимо после 2—3 иллюстраций на наборном полотне с дидактическим материалом приступать к работе с учебником.
На следующем уроке большее внимание должно быть уделено количественному и порядковому значению числа. Например, на наборном полотне выставлены в ряд кружки разных цветов: красный, синий, желтый, зеленый.
— Каким будет по счету зеленый кружок, если считать слева направо? Какой кружок стоит третьим слева (справа)? И т. д.
Показателем усвоения понятия числа на данном этапе является умение охарактеризовать каждое натуральное число.
— Что можно сказать о числе 5?
(5 стоит после 4 и перед 6; 5 больше всех предыдущих чисел: 5 > 4, 5 > 3 и т. д.; 5 меньше всех последующих чисел: 5 < 6, 5 < 7...; 5 — это 4 + 1, 3 + 2, 2 + 3, 1 + 4.)
Программой по математике предусмотрено в этой теме знакомство с числом и цифрой 0.
С числом и цифрой 0 учащиеся знакомятся после изучения числа 7 и ознакомления с понятием длины отрезка. Этому отводится специальный урок (см. с. 82—83), на котором доводится до сознания учащихся, что нуль есть характеристика пустого множества, а это значит, что и числовой фигуры тоже нет. Нам не нужен ни один кружок, камушек или точка, чтобы представить себе это число. Следовательно, пустая карточка будет характеризовать это число, если специально не оговорено что-то другое. Так, в примерах «с окошком» пустой квадратик не означает «нуль». Карточку же с цифрой 0 учитель, разумеется, покажет на этом уроке. И этого вполне достаточно, чтобы ребята хорошо запомнили эту цифру.
Понятие о нуле формируется на основе практических действий с предметными множествами. Нуль как характеристика пустого множества выступает в результате упражнений, показывающих, что, вычитая из какого-либо числа последовательно все его единицы, мы получаем все меньшие и меньшие числа и наконец, вычтя последнюю единицу, получаем нуль.
Выполнение соответствующих упражнений по рисункам учебника должно подвести детей к пониманию того, что 0 получается в результате вычитания 1 из 1, поэтому 0 < 1 и в ряду чисел должен занять место перед 1.
На этом же уроке рассматриваются свойства нуля: 0 + 1 = 1 и 1 – 0 = 1.
После ознакомления с числом 10 проводится работа по закреплению нумерации чисел первого десятка. К этому времени умение вести счет в пределах 10 (прямой и обратный) должно быть доведено у учащихся до автоматизма. Кроме того, они должны знать состав каждого числа первого десятка, уметь сравнивать эти числа.
С этими знаниями связываются геометрические представления о точке, прямой и отрезке, а также их обозначении, об измерении длин отрезков при помощи разных мерок.
Изучение прямой линии связано с очень важным понятием линейной протяженности, являющимся одним из существенных компонентов пространственных представлений. В учебнике формирование понятия «прямая линия» осуществляется постепенно. Впервые это понятие вводится еще в дочисловой период (с. 38—39). Здесь учащиеся учатся видеть такие линии в предметах окружающей обстановки (стороны классной доски, линия сгиба листа тетради, пересечение страниц в книге или тетради и т. п.), на рисунках и т. д. Затем, после ознакомления с числом 2, первоклассники на специально отведенном уроке (с. 50—51) продолжают изучение прямой, рассматривают способы обозначения, учатся соединять две точки прямой, проводя ее по клеточкам (если есть возможность) или по линейке. В ходе небольшой исследовательской работы первоклассники знакомятся со свойствами прямой: через одну точку можно провести много прямых, а через две — только одну прямую. При этом дети осознают явное отличие прямой от кривой линии.
К этому времени учащиеся уже умеют отмечать точки на прямой, обозначать их некоторыми заглавными буквами русского алфавита. Поэтому когда вводится понятие отрезка (с. 56—57) как части прямой, ограниченной двумя точками, и показывается его обозначение двумя буквами, то это не вызывает у первоклассников особых затруднений.
Главное — сначала научить детей отличать на чертеже прямую и отрезок прямой. Учащиеся постепенно усваивают, что концы отрезка отмечаются точками или штрихами, а у прямой таких условий при изображении нет.
По мере выполнения наблюдений и различных упражнений учащиеся подводятся к выводу, что отрезок прямой весь можно поместить на листе бумаги, а вот прямую так поместить на бумаге не удастся, какой бы большой лист бумаги мы ни взяли.
В этот период необходимо научить детей отыскивать в окружающей обстановке предметы (или их части), напоминающие отрезок. Это может быть край линейки, листа тетради, ребро шкафа, край кромки стола или классной доски и т. д.
Важными являются также упражнения на умение находить все отрезки на чертеже, называть имена отрезков, строить отрезок по двум заданным точкам.
При вычерчивании отрезков дети устанавливают между ними отношения «больше», «меньше» и «одинаковой длины» (или «равные»).
Например, пользуясь горизонтальными или вертикальными линиями тетради, они устанавливают, какой отрезок больше: верхний или нижний, крайний справа или крайний слева.

Далее первоклассники учатся сравнивать отрезки на глаз с последующей проверкой с помощью нити или бумажной полоски. В данном разделе вводится понятие «длина отрезка» и ее измерение. Но перед тем как познакомить детей с измерением отрезков с помощью мерок, они должны хорошо усвоить два способа сравнения длин предметов (полосок): путем наложения полос друг на друга и путем приложения их друг к другу.
Прежде всего учитель доводит до сознания детей, что отрезки можно измерять разными мерками. При этом выясняется, какую мерку удобнее использовать в каждом случае. Для этой цели учитель, заранее заготовив полоски длиной 30 см, 15 см и 7,5 см, ставит перед классом задачу.
— На доске начерчены 2 отрезка: зеленого и синего цвета. (Отрезки могут быть длиной 90 см и 120 см.) Они расположены так, что на глаз сравнить трудно. С помощью этой полоски (предлагается полоска в 30 см) выясните, какой из отрезков длиннее.
Прикладывая полоску сначала к одному отрезку, а затем к другому, учащиеся выясняют, что в зеленом отрезке она укладывается 3 раза, а в синем — 4 раза. Самостоятельно делают вывод: так как 4 > 3, то синий отрезок длиннее зеленого.
Далее учитель предлагает доказать тот же вывод, пользуясь второй меркой в 15 см.
В результате измерений учащиеся получают, что 8 > 6.
— А теперь, — говорит учитель, — я сделаю так: зеленый отрезок измерю второй меркой, а синий — первой меркой. Что же получается: 6 > 4, значит, зеленый отрезок больше синего? Может быть, мы допустили ошибку и поспешили с выводом?
При разборе данной ситуации ученики осознают, что для сравнения длин отрезков необходимо измерять их одной меркой.
УРОК 28. Число и цифра 3 (с. 58—59)
Цели урока:
1) показать образование числа 3, научить правильно соотносить цифру 3 с числом предметов, писать цифру 3;
2) повторить образование чисел 1 и 2, закрепить умение писать цифры 1 и 2.
ХОД УРОКА
1. Организационный момент.
2. Устные упражнения и практические работы.
1) Счет прямой и обратный от 1 до 10, от 6 до 10, от 7 до 3.
2) Игра «Покажи цифру».
Учитель поочередно показывает карточки с картинками, на которых изображены разные предметы в количестве 1 или 2. Дети в ответ поднимают и показывают карточки с соответствующими числами.
3) Повторение.
— Положите перед собой одну палочку.
— Сколько палочек надо добавить, чтобы их стало две? (Одну.)
— Положите еще одну палочку перед собой. Сколько всего? (Две.)
— Как получили? (К одной палочке прибавили еще одну палочку.)
3. Физкультминутка.
Скороговорка. В пруду у Поликарпа три карася, три карпа. (Повторяется трижды.)
4. Знакомство с числом 3.
1) Загадка.
| У него глаза цветные, Не глаза, а три огня. Он по очереди ими Сверху смотрит на меня. (Светофор.) |
— О чем идет речь? Сколько цветов у светофора? Назови их. Зачем нужен светофор?
— Положите перед собой два кружка. Добавьте еще один кружок. Сколько кружков стало? Как получили 3 кружка? (К двум прибавили еще один.)
— Число «три» обозначают цифрой 3. (Учитель показывает карточку с цифрой 3.)
— Где вы видели такую цифру? (Ответы детей.)
2) Работа по учебнику. (С. 58—59.)
Беседа по картинке с объяснительным материалом.
— Сколько цыплят у курицы вылупилось раньше? (2.)
— Сколько стало теперь? (3.)
— Как получилось 3 цыпленка? (2 + 1 = 3.)
— Какой цифрой мы обозначим число 3? Покажите. (Дети показывают карточку с цифрой 3.)
— Положите на стол 3 квадрата. Уберите 1 квадрат. Сколько квадратов осталось? (2.) Как получили 2? (3 – 1 = 2.)
Упр. 1, с. 58. Счет тройками. Здесь важно, чтобы дети осознали преимущества счета группами чисел. Полезно также предложить детям картинку, на которой изображены 6 пар коньков и 2 тройки хоккеистов.
— Кого на картинке удобно считать тройками? (Хоккеистов.)
— Сколько троек хоккеистов на поле? (2 тройки.)
— Сколько всего хоккеистов? (6.)
— Что на картинке мы будем считать парами? (Коньки.)
— Сколько пар коньков вы видите? (6 пар.)
— Хватит ли каждому хоккеисту по паре коньков? (Да.)
Упр. 2, с. 58. Это задание направлено на усвоение места числа 3 в числовом ряду, формирование зрительного образа расположения чисел 1, 2 и 3 на числовой прямой и закрепление представлений о взаимном расположении точек на прямой (справа, слева, между).
Упр. 3, с. 59. Все возможные варианты уплаты 3 рублей показываются детьми с помощью монет из Приложения: 1 + 1 + 1, 2 + 1, 1 + 2.
Упр. 4, с. 59. После рассмотрения иллюстрации в учебнике дети сами придумывают и рисуют в тетради другие фигуры из трех клеток.
5. Физкультминутка.
| Белка шла, шла, шла, Белый гриб нашла. Раз грибок, два грибок, три грибок. Положила в кузовок. |
6. Работа в тетради. Письмо цифры 3.
7. Физкультминутка.
| Еж по лесу шел, шел, шел. На обед грибы нашел. Два — под березой, Один — у осины. Сколько грибов в плетеной корзине? |
8. Работа по учебнику. (Продолжение.)
Выборочное выполнение заданий № 5—6, с. 59.
9. Итог урока.
УРОК 3 (вторая четверть).
Число и цифра 7 (Часть 1, с. 78—79)
Цели урока:
1) показать образование числа 7, научить соотносить цифру 7 с числом предметов, писать цифру 7;
2) повторить образование чисел 1, 2, 3, 4, 5 и 6, закрепить умение писать цифры 5 и 6.
ХОД УРОКА
1. Организационный момент.
2. Устные упражнения и практические работы.
1) Счет прямой и обратный от 1 до 10, от 5 до 9, от 7 до 2.
2) Игра «Покажи цифру».
Учитель поочередно показывает карточки с картинками, на которых изображены разные предметы в количестве от 1 до 6. Дети в ответ поднимают и показывают карточки с соответствующими цифрами.
3) Повторение.
— Положите перед собой 5 палочек.
— Сколько палочек надо добавить, чтобы их стало 6? (Одну.)
— Положите еще одну палочку перед собой. Сколько всего? (6.)
— Как получили? (К 5 палочкам прибавили 1 палочку.)
3. Подготовка к знакомству с числом 7.
— Сегодня на уроке у нас гости: Белоснежка и гномики. На наш урок математики они принесли разные задания из сказочной школы. Попробуйте справиться с ними.
1-й гном.
— На доске выставлен ряд чисел:

Какое число заблудилось? Где его место? Переставьте нужные карточки.
2-й гном.
— С помощью кассы цифр покажите самое маленькое число в ряду от 1 до 6; самое большое число. Покажите число, которое стоит слева от 2, справа от 5. Покажите число между 3 и 5, следующее за ним число, число, которое стоит перед 4.
3-й гном.
— Я задумал число, прибавил к нему 1 и получил 6. Какое число я задумал?
4-й гном.
— Сколько дней в неделе? Какой день недели сегодня? Как называют день недели, который будет завтра? который был вчера? Назовите дни недели по порядку, начиная с понедельника. (По ходу ответов учеников учитель прикрепляет к доске таблички со словами: понедельник, вторник, среда, четверг, пятница, суббота, воскресенье. См. учебник на с. 79, № 5.)
5-й гном.
— Отгадайте загадку: «Красивое коромысло над рекою повисло». (Радуга.) (На доске вывешивается картинка с изображением радуги.)
— Сколько цветов у радуги? Какие? (Дети отвечают, а учитель выставляет на доске в виде ромашки 7 цветных кружков: красный, оранжевый, желтый, зеленый, голубой, синий, фиолетовый.)
6-й гном.
— Как бы вы назвали этот цветок? (Дети могут предлагать разные названия, но желательно остановиться на имени «Цветик-семицветик».) Объясните, почему его так назвали.
7-й гном.
— Кто догадался, о каком числе мы будем сегодня говорить? (7.)
— Положите перед собой 6 палочек. Добавьте еще одну палочку. Сколько стало? Как получили 7 палочек? (К 6 палочкам прибавили еще 1 палочку.)
Белоснежка.
— Число семь обозначают цифрой 7. (Показывает карточку с цифрой 7.)
— Где вы видели такую цифру? (Ответы детей.)
4. Физкультминутка.
| Сколько гномиков у нас, Столько и подпрыгнем раз. Сколько здесь цветных кругов, Столько сделаем хлопков. |
5. Работа по учебнику. (С. 78—79.)
Беседа по картинке с объяснительным материалом.
— Сколько цыплят у курицы вылупилось раньше? (6.)
— Сколько стало теперь? (7.)
— Как получилось 7 цыплят? (6 + 1 = 7.)
— Какой цифрой мы обозначим число 7? Покажите. (Дети показывают карточку с цифрой 7.)
— Положите на стол 7 квадратов. Уберите 1 квадрат. Сколько квадратов осталось? (6.) Как получили 6? (7–1 = 6.)
Упр. 1, с. 78. Задание направлено на выяснение состава числа 7. Раскладывая 7 семечек в две тарелки, дети перебирают все возможные способы и приходят к выводу, что 7 — это 6 и 1, 5 и 2, 4 и 3, 3 и 4, 2 и 5, 1 и 6.
Упр. 2, с. 78. Это задание имеет целью познакомить учащихся с местом числа 7 в числовом ряду, закрепить представления о взаимном расположении чисел от 1 до 7 на прямой.
Упр. 3, с. 78. Все возможные варианты уплаты 7 рублей показываются детьми с помощью монет из Приложения.
Упр. 4, с. 79. После рассмотрения иллюстрации в учебнике дети сами придумывают и рисуют в тетради другие фигуры из семи клеток.
6. Физкультминутка.
| Раз — подняться, подтянуться, Два — согнуться, разогнуться, Три — в ладоши три хлопка, Головою три кивка. На четыре — руки шире, Пять — руками помахать, Шесть — за парту сесть опять, Семь — начинаем мы писать. |
7. Работа в тетради. Письмо цифры 7.
8. Физкультминутка.
| Раз, два, три, четыре, пять, Надоело нам писать. Мы немножко постоим, Отдохнем и помолчим. А потом опять Из учебника решать. |
9. Работа с учебником. (Продолжение.)
10. Итог урока.
УРОК-ПУТЕШЕСТВИЕ:
«В гостях у десятка» (с. 90—91)
Цели урока:
1) закрепить знания учащихся о нумерации чисел первого десятка, состав чисел в пределах 10, навыки счета;
2) развивать наблюдательность, смекалку и фантазию.
Материалы и оборудование:
1. Бумажные модели ракет (3 штуки) с отверстием в виде иллюминатора.
2. Кроссворд.
3. Изображения Белочки, Деда Мороза, Золушки, Карлсона, Мышки, Паровоза.
4. 2 набора цифр от 1 до 9 с буквами на оборотной стороне.
5. Касса цифр.
6. Круговой пример с прорезями для карточек с ответами.
ХОД УРОКА
1. Организационный момент. Подготовка к путешествию на сказочную, веселую планету Математика.
2. Игра-эстафета «Запуск ракеты».
— Итак, в путь! Начнем наше необычное путешествие на планету Математика. (Учитель показывает на красочно оформленную доску.)
| Весело живут на той планете Взрослые и дети. Управляют там мальчишки, Хитроумные братишки. Десять их, но братья эти Сосчитают все на свете. |
— Кто же главный на планете Математика? К кому мы полетим? (Числа.)
— Планета эта находится очень далеко от Земли. И лететь нам придется на ракете. Сколько ракет приготовлено к старту? (3.)
— Правильно! Каждый ряд полетит на своей ракете.
3. Выполнение логических упражнений на нумерацию.
— Наконец мы поднялись в небо. Летим день, летим другой, третий... И вот в иллюминаторе показалась планета.
Учитель вставляет в иллюминаторы ракет по одному кругу с заданием и поясняет, что задания разные, так как каждая ракета видит планету со своей стороны.
— Найдите на картинке все цифры от 0 до 9. (На каждом из трех рисунков вразброс даны цифры от 0 до 9 разного цвета, размера, начертания.)

— Мы выполнили все задания и спустились на планету Математика. Вокруг нас цифры. Они приветствуют нас, дарят нам свои фотографии. Не верите, загляните в свои тетради.
Учащиеся находят в учебнике или тетради открытки с цифрами от 1 до 9.
— А у меня, ребята, две фотографии цифр. (Учитель читает стихи и демонстрирует две карточки из кассы цифр.)
| Цифра вроде буквы О — Это ноль, иль ничего. Круглый ноль такой хорошенький, Но не значит ничегошеньки! Если ж слева рядом с ним Единицу примостим, Он побольше станет весить, Потому что это — десять. (С. Маршак) |
— Это число нам хорошо знакомо. Вы знаете, как оно записывается, как читается. Умеете считать до 10, решать примеры и задачи, знаете состав 10 и умеете дополнять любое однозначное число до 10.
Десяток будет вашим экскурсоводом на планете Математика. Он вместе с учебником поможет вам выбрать наиболее интересный маршрут. От имени Десятка учитель обращается к детям со словами:
| Считайте, ребята, точнее считайте, Хорошее дело смелей прибавляйте, Плохие дела поскорей вычитайте. Учебник научит вас точному счету, Скорей за работу, скорей за работу! (Ю. Яковлев) |
Затем учитель просит учащихся выставить по порядку карточки-фотографии цифр сначала с красными цифрами, а потом с синими. На доске появляются два набора карточек.

По команде учителя один ученик переворачивает оборотной стороной красные карточки, а другой — синие, и учащиеся узнают следующий вид заданий, который задал Десяток: ОТГАДАЙТЕ КРОССВОРД.

4. Отгадывание кроссворда. Выполнение упражнений учебника (с. 90, № 1—7).
1) Десяток задает ученикам загадку, ответ на которую есть первое слово кроссворда:
| По десятку на шесточке Сели умные кружочки И считают громко вслух. Только слышно: стук да стук! (Счеты.) |
Далее учитель предлагает детям показать Десятку, как они знают состав числа 9, и выполнить задание № 1 на с. 90.
2) Второе слово кроссворда — ответ к загадке:
| Старик у ворот Тепло уволок, Сам не бежит И стоять не велит. (Мороз.) |
Учитель вспоминает с учащимися о предстоящем празднике Нового года, о Деде Морозе и, показывая на картинку к упражнению № 2 учебника, говорит:
| Мы на елке веселились, И плясали, и резвились. После добрый Дед Мороз Нам подарки преподнес. Дал большущие пакеты, В них же всякие предметы. Стали мы пакет вскрывать, Содержимое считать: Два квадрата очень синих... |
(Далее дети вместе с учителем продолжают перечислять: два синих маленьких треугольника, пять желтых маленьких треугольников, один большой желтый треугольник.)
| Все лежит в пакетах этих! Сколько ж в них фигурок, дети? |
Затем дети определяют, по какому признаку Дед Мороз разделил эти фигуры на два пакета, и дают пояснения к соответствующим примерам.
3) Чтобы узнать третье слово кроссворда, ученики разгадывают загадку Деда