Приложения определенного интеграла
а) Площадь фигуры
Как уже отмечалось,  численно равен площади криволинейной трапеции, ограниченной кривой у = f (x), f (x) ≥ 0, прямыми х = а, х = b и отрезком [ a, b ] оси ОХ (рисунок 1).
численно равен площади криволинейной трапеции, ограниченной кривой у = f (x), f (x) ≥ 0, прямыми х = а, х = b и отрезком [ a, b ] оси ОХ (рисунок 1).
 (1)
(1)
| у |
| у=f (x) |
| a |
| b |
| Рис.2 |
| х |
| х |
| у |
| а |
| b |
| у = f (x) |
| Рисунок 1 |
Учитывая свойства определенного интеграла, эту геометрическую интерпретацию можно обобщить и на случай f (x) £ 0(рис.2). А именно, если f (x) £ 0 на [ a, b ], то
 (2)
(2)
Т.е. площадь криволинейной трапеции, расположенной под осью ОХ, равна соответствующему интегралу, взятому со знаком минус.
Если же на заданном отрезке функция у = f (x) меняет знак, то для вычисления площади фигуры, заключенной между графиком этой функции и осью ОХ, следует разбить отрезок на части, на каждой из которых функция сохраняет знак, и найти площадь каждой части фигуры. Искомая площадь в этом случае есть алгебраическая сумма интегралов по этим отрезкам, причем интегралы, соответствующие отрицательным значения функции, взяты в этой сумме со знаком минус (рис.3):

 –
– 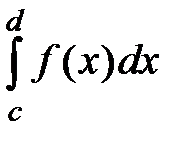 +
+  (3)
(3)
| B |
| C |
| A |
| b |
| d |
| a |
| c |
| + |
| – |
| + |
| Рис.3 |
Если фигура ограничена двумя кривыми у = f 1(x) и у = f 2(x), f 1(x) £ f 2(x) то, как следует из рисунка 4, ее площадь равна разности площадей криволинейных трапеций а ВС b и а АD b, каждая из которых численно равна интегралу. Значит,  .
.
Таким образом,  (4)
(4)
| у = f 1(x) |
| у = f 2(x) |
| b |
| а |
| A |
| B |
| C |
| D |
| Рис.4 |
S = 
(докажите это!). Подумайте, как вычислить площадь фигуры, изображенной на рисунке 5б?
| а |
| у = f 1(x) |
| у = f 1(x) |
| у = f 2(x) |
| у = f 2(x) |
| b |
| b |
| а |
| б) |
| а) |
| Рисунок 5 |
Мы вели речь только о криволинейных трапециях, прилежащих к оси ОХ. Но аналогичные формулы справедливы и для фигур, прилежащих к оси ОУ. Например, площадь фигуры, изображенной на рисунке 6а, находится по формуле
S = 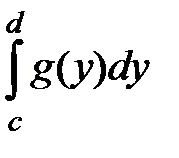 . (5)
. (5)
| x = g (y) |
| d |
| c |
| х |
| у |
| а) |
| x = g 2(y) |
| d |
| c |
| х |
| у |
| x = g 1(y) |
| б) |
| Рисунок 6 |
 ,
,  и прямыми
и прямыми  ,
,  (рисунок 6б), то площадь этой области можно найти по формуле
(рисунок 6б), то площадь этой области можно найти по формуле
 (6)
(6)
Если линия, ограничивающая криволинейную трапецию, задана параметрическими уравнениями  , то площадьэтой криволинейной трапеции равна
, то площадьэтой криволинейной трапеции равна
| В |
| А |
| О |
| р |
| r = r (j) |
| a |
| b |
| Рис.7 |
 . (7)
. (7)
Рассмотрим полярную систему координат. Фигура ОАВ, ограниченная лучами j=a, j=b и кривой r = r (j) (рисунок 7) называется криволинейным сектором. Площадь криволинейного сектора ОАВ находится по формуле
S =  (8)
(8)
б) Длина дуги кривой
Пусть дана кривая у = f (x). Рассмотрим дугу (рисунок 8а). Длина этой дуги кривой находится по формуле
l =  . (9)
. (9)
Если кривая задана уравнением  , и рассматривается дуга
, и рассматривается дуга  этой кривой, соответствующая изменению у на отрезке [ с, d ] (рисунок 8б), длина этой дуги может быть найдена по формуле
этой кривой, соответствующая изменению у на отрезке [ с, d ] (рисунок 8б), длина этой дуги может быть найдена по формуле
l =  . (10)
. (10)
| а |
| b |
| A |
| B |
| х |
| у |
| а) |
| с |
| d |
| A |
| B |
| х |
| у |

|
| у = f (x) |
| Рис.8 |
| б) |
Если кривая задана параметрически  , то длина дуги этой кривой, соответствующей изменению параметра t Î[a, b], находится по формуле
, то длина дуги этой кривой, соответствующей изменению параметра t Î[a, b], находится по формуле
 (11)
(11)
Если дуга кривой задана в полярной системе координат уравнением  , jÎ[a, b], то
, jÎ[a, b], то
 (12)
(12)
| Рис.9 |
| а |
| b |
| x |
| A |
| B |
Рассмотрим криволинейную трапецию а АВ b, ограниченную линией у = f (x), прямыми х = а, х = b и отрезком [ a, b ] оси ОХ (рис.9). Пусть эта трапеция вращается вокруг оси ОХ, в результате получится тело вращения, объем которого выражается формулой
| Рис.10 |
| с |
| d |
| х = j(у), |
 (13)
(13)
Аналогично можно записать формулу объема тела, полученного вращением вокруг оси ОУ криволинейной трапеции, ограниченной графиком функции х = j(у), прямыми y = c, y = d и отрезком [ c, d ] оси ОУ (рис.10):
 (14)
(14)
Пример 1.
Построить фигуру, ограниченную линиями, и найти ее площадь:
а)  ,
,  ,
,  ,
,  ; б)
; б)  ,
,  ,
,  ,
,  ;
;
в)  ,
,  ; г)
; г)  ,
,  ,
,  .
.

|
| х |
| у |
| Рис.11 |
 ,
,  ,
,  ,
,  (рисунок 11). Площадь полученной криволинейной трапеции найдем по формуле (1):
(рисунок 11). Площадь полученной криволинейной трапеции найдем по формуле (1):  , где
, где 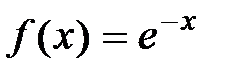 ,
,  ,
,  .
.
Получим
 (кв.ед).
(кв.ед).
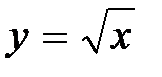
|
| х |
| у |
| Рис.12 |
б) Построим линии  ,
,  ,
,  ,
,  (рисунок 12). Фигура, ограниченная данными линиями, есть криволинейная трапеция, прилежащая к оси О у, поэтому для вычисления её площади воспользуемся формулой (5): S =
(рисунок 12). Фигура, ограниченная данными линиями, есть криволинейная трапеция, прилежащая к оси О у, поэтому для вычисления её площади воспользуемся формулой (5): S = 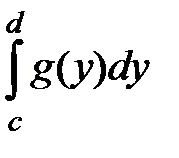 . Здесь
. Здесь  ,
,  , а функцию
, а функцию  получим из уравнения линии
получим из уравнения линии  , если выразим х через у:
, если выразим х через у:  Тогда имеем
Тогда имеем
 (кв.ед).
(кв.ед).
в) Построим линии  ,
,  . Линия
. Линия  есть прямая (биссектриса I и III координатных углов).
есть прямая (биссектриса I и III координатных углов).
Линия  есть парабола, чтобы изобразить её, найдем вершину и точки пересечения параболы с осями координат. Известно, что если парабола имеет уравнение
есть парабола, чтобы изобразить её, найдем вершину и точки пересечения параболы с осями координат. Известно, что если парабола имеет уравнение  , то абсцисса её вершины равна
, то абсцисса её вершины равна  . В случае параболы
. В случае параболы 
 . Тогда абсцисса вершины
. Тогда абсцисса вершины  , а ордината
, а ордината  . Таким образом, вершина параболы – точка (1, 1). Точки пересечения параболы с осью О х найдем из уравнения
. Таким образом, вершина параболы – точка (1, 1). Точки пересечения параболы с осью О х найдем из уравнения  :
:  . Значит, парабола пересекает ось О х в точках (0, 0) и (2, 0). Точка (0, 0) одновременно есть точка пересечения параболы с осью О у.
. Значит, парабола пересекает ось О х в точках (0, 0) и (2, 0). Точка (0, 0) одновременно есть точка пересечения параболы с осью О у.

|
| х |
| у |
| у=х |
| Рис.13 |
 .
.
Здесь  ,
,  . Границы а и b интервала интегрирования можно определить по построению. А можно найти формально как абсциссы точек пересечения данных линий:
. Границы а и b интервала интегрирования можно определить по построению. А можно найти формально как абсциссы точек пересечения данных линий:
 .
.
Тогда получим
 (кв.ед).
(кв.ед).
г) Построим линии  ,
,  ,
,  . Линия
. Линия  есть парабола, которая получается из параболы
есть парабола, которая получается из параболы 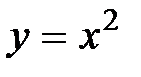 сдвигом всех точек вдоль оси О х на единицу влево. Парабола
сдвигом всех точек вдоль оси О х на единицу влево. Парабола  получается из параболы
получается из параболы  сдвигом вдоль оси О у на единицу вверх. Линия
сдвигом вдоль оси О у на единицу вверх. Линия  есть ось О х. Получим область АВС, изображенную на рисунке 14. Площадь этой области можно найти двумя способами.
есть ось О х. Получим область АВС, изображенную на рисунке 14. Площадь этой области можно найти двумя способами.
| х |
| у |

|

|
| О |
| –1 |
| Рисунок 14 |
| А |
| В |
| С |
 (кв.ед.)
(кв.ед.)
2 способ. Площадь области АВС можно найти по формуле (6):
 .
.
Найдем функции  и
и  , графики которых ограничивают данную область:
, графики которых ограничивают данную область:
 Þ
Þ 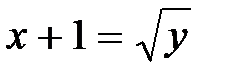 Þ
Þ 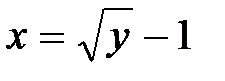 Þ
Þ  ;
;
 Þ
Þ  Þ
Þ  Þ
Þ  .
.
При этом, как видно из рисунка 14, 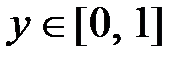 .
.
Тогда

 (кв.ед.)
(кв.ед.)
Как видим, получили тот же ответ.
Пример 2.
Найти длину дуги кривой:
а) 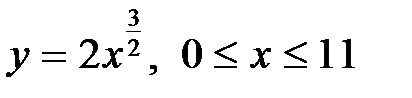 б)
б)  ;
;
в)  .
.
Решение.
а) Поскольку линия задана уравнение вида  , воспользуемся формулой (9):
, воспользуемся формулой (9):
l =  ,
,
где  ,
,  . Но для этого сначала нужно найти
. Но для этого сначала нужно найти  . Имеем
. Имеем
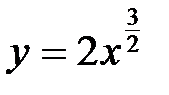 Þ
Þ 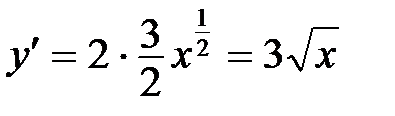 ,
,
поэтому  . Тогда
. Тогда
l = 
 (ед.дл.).
(ед.дл.).
б)  . Здесь используем также формулу (9), считая
. Здесь используем также формулу (9), считая  ,
,  . Находим
. Находим
 ,
,  ,
,
 ,
,
 .
.
Тогда получим
l = 

 (ед.дл.)
(ед.дл.)
в) Линия  задана уравнением вида
задана уравнением вида  , поэтому используем формулу
, поэтому используем формулу
l =  ,
,
где  ,
,  . Находим
. Находим
 ,
,  ,
,
 ,
,
 .
.
Тогда
l = 

 (ед.дл.)
(ед.дл.)
Пример 3.
Найти дину дуги линии:
а)  б)
б) 
Решение.
а) Линия задана параметрически, поэтому будем использовать формулу (11)  . Заметим, что границы изменения параметра t не указаны, но оговорено, что дуга описывается заданными формулами только при
. Заметим, что границы изменения параметра t не указаны, но оговорено, что дуга описывается заданными формулами только при  – значит, исходя из этого требования нужно найти отрезок изменения t. Имеем:
– значит, исходя из этого требования нужно найти отрезок изменения t. Имеем:
 .
.
Находим
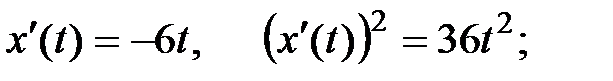
 ;
;
 .
.
Поскольку  , то
, то 
Тогда




 (ед.дл.).
(ед.дл.).
б)  Здесь линия также задана параметрически, значит, вновь будем использовать формулу (11)
Здесь линия также задана параметрически, значит, вновь будем использовать формулу (11)  . Найдем
. Найдем
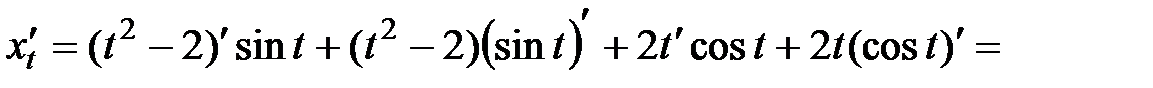
 ;
;

 .
.
Тогда  .
.
Следовательно
 (ед. дл.)
(ед. дл.)
Пример 4.
Вычислить объем тела, полученного вращением фигуры, ограниченной линиями вокруг оси Ох.
Решение.
| Рис.15 |
| С |
| х |
| у |
| О |
| А |
| В |

 есть область ОАВС (рисунок 15). По формуле (13)
есть область ОАВС (рисунок 15). По формуле (13)  искомый объем тела, полученного в результате вращения этой фигуры, равен
искомый объем тела, полученного в результате вращения этой фигуры, равен
 (ед.2)
(ед.2)
Пример 5.
| Рис.16 |
| -2 |
| С |
| х |
| у |
| О |
| А |
| В |
| D |
 , отрезком
, отрезком  оси О х и отрезком прямой
оси О х и отрезком прямой  . Найти объём тела, образованного вращением этой фигуры вокруг оси О х.
. Найти объём тела, образованного вращением этой фигуры вокруг оси О х.
Фигура, ограниченная дугой параболы  , отрезком
, отрезком  оси О х и отрезком прямой
оси О х и отрезком прямой  , изображена на рисунке 16. Найдем абсциссу точки С пересечения параболы
, изображена на рисунке 16. Найдем абсциссу точки С пересечения параболы  с прямой
с прямой  :
:

 Þ
Þ
Þ  .
.
Следовательно, С(1,3). Искомый объем равен разности объёмов V1 и V2 тел, образованных вращением криволинейной трапеции АВСD и треугольника ОСD. По формуле (13)  находим:
находим:
V1= 
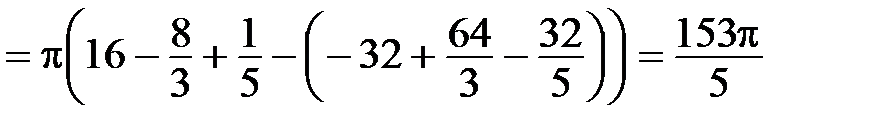 ,
,
V2  .
.
Тогда искомый объем равен
V1 – V2 =  (куб.ед).
(куб.ед).