Программирование циклических вычислительных процессов

Задание №2

Программирование ветвящихся вычислительных процессов

Цель работы

Получить навыки программирования ветвящихся вычислительных процессов. Изучить условные операторы, переменные логического типа, логические отношения и операции.

 

Задание

Пусть на плоскости x, y задана область D. Требуется определить «попадает» ли точка с координатами (x, y) в область D или нет. Если попадает, то необходимо вычислить функцию и переменной M, значение которой является признаком «попадания» или «непопадания», присвоить значение M=1. В противном случае вычислить и положить M=2.

 

Ход работы

Алгоритм решения поставленной задачи:

1. Выписать область D и выписать функци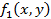и и

2. Записать уравнения, определяющие границы области

3. Подготовить 7 точек, чтобы часть точек находилась внутри D, а часть- вне ее.

4. Написать программу для выполнения поставленной задачи.

5. Для выбранных точек получить и записать результаты счета.

Задание:

f₁₌tg(x)/e^y f₂=

2.Если:

(x>0 и y>0 и X**2+Y**2<=9) или (x<0 и y>0 и y<=x+4) или (x<0 и y<0 и x>(-4) и y>(-2))

то точка принадлежит области D

1)(1;1)
2)(3;3)
3)(-1;2)
4)(-5;2)
5)(-2;-1)
6)(-5;-3)

7)(3;-3)

 

		Fortran	MathCAD
x	y	z	m	c	z	m	c
		0.1573E+01		T	1.573
		0.0751E+01		F	0.751
-1		-0.1211E+01		T	-1.211
-5		0.083E+01		F	0.83
-2	-1	0. 394E+01		T	3.94
-5	-3	0.0282E+01		F	0.282
	-3	0. 0271E+01		F	0.271

 

PROGRAM LAB2

LOGICAL C

REAL X,Y,Z

INTEGER I,M

DO I=1,8

PRINT *,'X=?,Y=?';READ *,X,Y

C=(x>0..and. y>0..and.X**2+Y**2<=9).or.(x<0..and.y>0..and.y<=x+4).or.(x<0..and.y<0..and.x>(-4).and.y>(-2))

IF(C)THEN

PRINT*,'YES'

Z=F1(X,Y);M=1

ELSE

PRINT *,'NO'

Z=F2(X,Y);M=2

END IF

PRINT 2,X,Y,Z,C,M

END DO

2 FORMAT ('X=',F7.3,3X,'Y=',F7.3,3X,'Z=',E11.4,3X,'C=',L2,3X,'M=',I2/)

END PROGRAM LAB2

FUNCTION F1(X,Y)

F1=tan(x)/exp(x)**y

END FUNCTION F1

FUNCTION F2(X,Y)

F2= (sqrt(sin(2*x+3*y)**2)**1./3.)

END FUNCTION F2

MATHCAD

 

 

 

program Lab2

real:: a,b,c

logical:: q,w,e

print*,'a,b,c=?';read '(2F7.3)',a,b,c

do i=1,8

q=a>b.and.a<c.or.&

a<b.and.a>c

w=b>a.and.b<c.or.&

b<a.and.b>c

e=c>a.and.c<b.or.&

c<a.and.c>b

if(q) then

print*,a

elseif(w) then

print*,b

elseif(e) then

print*,c

else

print*,'no'

end if

end do

end

 

28.,558.,345. 345.0000

Задание №3

Программирование циклических вычислительных процессов

Цель работы

Получить навыки программирования циклических вычислительных процессов. Изучить циклы с шагом и циклы с условием.

Задание

1. Записать расчетные формулы для вычисления слагаемого и конечной суммы

ряда

2. Составить алгоритм вычисления с заданной точностью суммы конечного числа членов ряда в указанном диапазоне изменения параметра x с заданным шагом. Для получения шага диапазон изменения x разделить на 10.

3. Составить программу решения задачи. В программе для каждого значения x предусмотреть вычисление как приближенной, так и точной суммы соответствующего ряда y по приведенной в таблице формуле.

4. Отладить и просчитать программу. Результат получить в виде таблицы, содержащей для каждого x из указанного диапазона приближенное и

точное значения суммы ряда, а также количество просуммированных членов.

 

Ход работы

1. Задать x0-начало цикла и xл-конец цикла

2. Задаем шаг h по формуле

3. Рассчитать формулы для вычисление слагаемого и конечной суммы ряда

4. Составить программу решения задач рекуррентным способом

5. Построить таблицу полученных данных

 

Задание:

Формула ряда: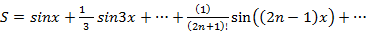

Формула точного вычисления суммы: π/4

1. x0= π/10 xk=9 π/10

2. h=0,09

3.

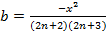
Fortran

program Lab3

real:: a,b,c,eps,h,s,x,x0,xk,y,p

integer:: i,n

pi=3.1415926535

x0=pi/10

xk=9*pi/10

eps=0.0001

h=(xk-x0)/10

do i=0,10

x=x0+h*i

n=0;a=x;s=0.

do

b=(sin*(x)*(2*n)-1+sin*((2*n-1)*x))/4*n-2

s=s+a

a=a*b

n=n+1;

if(abs(a)<eps)exit

end do

y=pi/4

print 2,x,s,y,n; write(1,2)x,s,y,n

end do 2 format('x=',f6.3,3x,'s=',e10.3,3x,'y=',e10.3,3x,'n=',i5)

end program lab3

 

 

1.

 

x	S(x)	y
0.314	0.324	0.785
0.565	0.622	0.785
0.817	0.979	0.785
1.068	1.404	0.785
1.319	1.43	0.785
1.57	-19.257	0.785
1.821	-533.961	0.785
2.072	-8.624E+3	0.785
2.324	-9.986E+4	0.785
2.575	-8.928E+5	0.785
2.826	-6.477E+6	0.785