ЛЕКЦИЯ
Геометрические приложения определенного интеграла
| 1. Площадь плоской фигуры в декартовых и полярных координатах и для кривой, заданной параметрически 2. Длина дуги кривой 3. Площадь поверхности вращения 4. Объем тела с заданным поперечным сечением. Объем тела |
вращения
Содержание
Введение
На предыдущих лекциях мыввели понятие определенного интеграла как предела интегральных сумм, вывели формулу Ньютона-Лейбница для более простого вычисления определенного интеграла. Теперь мы можем рассмотреть ряд задач, связанных с геометрическим приложением определенного интеграла. Следует отметить, что для их решения применяется один и тот же вычислительный метод: разбиение фигуры на 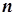 частей, приближенное решение задачи для каждой части, суммирование и предельный переход.
частей, приближенное решение задачи для каждой части, суммирование и предельный переход.
1. Площадь плоской фигуры в декартовых и полярных координатах и для кривой, заданной параметрически
2.
1.1 Кривая задана в виде  .
.
Известно, что площадь фигуры, ограниченной линией  ; прямыми
; прямыми 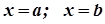 , осью
, осью  вычисляется по формуле:
вычисляется по формуле:
Если  , то
, то  ;
;
если функция 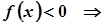
 ;
;
 если функция
если функция  на
на  меняет знак конечное число раз, то площадь
меняет знак конечное число раз, то площадь  или надо найти сумму абсолютных величин определенных интегралов.
или надо найти сумму абсолютных величин определенных интегралов.
Если область ограничена кривыми  , прямыми
, прямыми 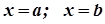 причем на
причем на  ;
; 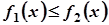 , то
, то



1.2 Пусть функция  задана параметрически на
задана параметрически на  , т.е.
, т.е.
 , где
, где  ; причем
; причем 
Так как 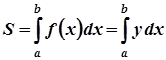 , то сделав подстановку
, то сделав подстановку  , а
, а  , получим
, получим 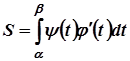
1.3 Пусть кривая задана в полярной системе координат

Площадь криволинейного сектора, ограниченного кривой  и радиус – векторами
и радиус – векторами  вычисляется по формуле
вычисляется по формуле
| |||
 | |||
Пример 1. Найти площадь фигуры, ограниченной кривыми: 
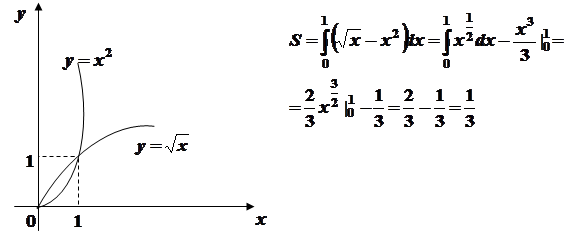 |
Длина дуги кривой
Пусть дана кривая  . Найдем ее длину на отрезке
. Найдем ее длину на отрезке  .
.
 |
Для решения поставленной задачи разобьем дугу  точками
точками
 .
.
Получим ломаную, вписанную в дугу  . Обозначим длину каждого звена ломаной через
. Обозначим длину каждого звена ломаной через  , а через
, а через  .
.
О.2.1. Длиной  кривой
кривой  называется предел, к которому стремится длина вписанной ломаной, когда длина наибольшего звена ломаной
называется предел, к которому стремится длина вписанной ломаной, когда длина наибольшего звена ломаной  стремится к нулю.
стремится к нулю.
Пусть функция  непрерывна на
непрерывна на  вместе с первой производной. Обозначим
вместе с первой производной. Обозначим  и
и  . Тогда по теореме Пифагора из прямоугольного треугольника с катетами
. Тогда по теореме Пифагора из прямоугольного треугольника с катетами  и
и  найдем
найдем
 .
.
Используя теорему Лагранжа, получим
 , где
, где  . Тогда
. Тогда
 .
.
Длина всей ломаной  . Так как функция
. Так как функция  непрерывна, то предел полученной интегральной суммы существует и равен длине кривой
непрерывна, то предел полученной интегральной суммы существует и равен длине кривой  .
.
 .
.
Таким образом, длина дуги кривой в декартовой системе координат находится по формуле
 . (1)
. (1)
2.2. Пусть функция  задана параметрически на
задана параметрически на  , т.е.
, т.е.
 , где
, где  ; причем
; причем  , функции
, функции  и
и  непрерывны и имеют первые непрерывные производные.
непрерывны и имеют первые непрерывные производные.
Известно, что
 ,
,  .
.
Тогда  (2)
(2)
2.3. Пусть кривая задана в полярной системе координат
 ,
,  . Используя формулы перехода от полярной к декартовой системе координат, получим:
. Используя формулы перехода от полярной к декартовой системе координат, получим:
 - параметрическое задание кривой. Используя формулу (2), найдем
- параметрическое задание кривой. Используя формулу (2), найдем
 ;
;
 .
.
Тогда длина дуги кривой в полярных координатах имеет вид 
Теперь можем перейти в нахождению площади поверхности вращения.
Площадь поверхности тела вращения
Требуется вычислить площадь поверхности тела, образованного вращением участка  кривой
кривой  вокруг оси
вокруг оси  .
.
Разобьем  на части точками
на части точками 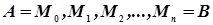 . Соединим точки деления хордами. Обозначим длину каждой хорды через
. Соединим точки деления хордами. Обозначим длину каждой хорды через 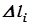
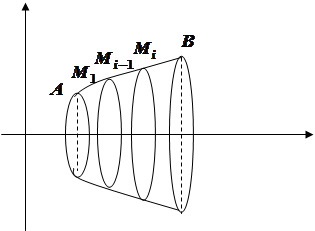 |
В результате вращения каждой хорды вокруг оси  получим усеченный конус, площадь поверхности которого равна произведению длины окружности среднего сечения на образующую, т.е.
получим усеченный конус, площадь поверхности которого равна произведению длины окружности среднего сечения на образующую, т.е.

Известно, что 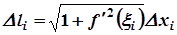 , где
, где  , поэтому
, поэтому

Площадь поверхности всей фигуры будет равна

Предел этой суммы (если он существует) и называется площадью поверхности тела вращения.
Однако, полученная сумма не является интегральной для функции  , но можно доказать, что предел интегральной суммы для этой функции будет равен пределу указанной суммы
, но можно доказать, что предел интегральной суммы для этой функции будет равен пределу указанной суммы  .
.
Преобразуем  к одной точке
к одной точке 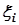
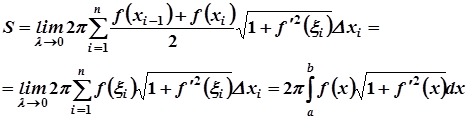
где 

В параметрической форме

В полярной системе координат

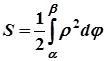 т.к. площадь кругового сегмента равна
т.к. площадь кругового сегмента равна  - центральный угол
- центральный угол