Степенные ряды.
Среди функциональных рядов есть класс степенных и тригонометрических рядов.
Определение. Функциональный ряд вида

называется степенным по степеням  . Выражения
. Выражения  - постоянные числа.
- постоянные числа.
Если 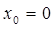 ряд
ряд  является степенным по степеням
является степенным по степеням  .
.
Область сходимости степенного ряда. Теорема Абеля.
Теорема. Если степенной ряд 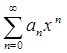 сходится в точке
сходится в точке  , то он сходится и притом абсолютно для всякого значения
, то он сходится и притом абсолютно для всякого значения  , по абсолютной величине меньшего
, по абсолютной величине меньшего  , то есть
, то есть  или в интервале
или в интервале  .
.
Доказательство.
Вследствие сходимости рада 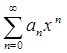 его общий член должен стремиться к нулю, поэтому все члены этого ряда равномерно ограничены: существует такое постоянное положительное число
его общий член должен стремиться к нулю, поэтому все члены этого ряда равномерно ограничены: существует такое постоянное положительное число  , что при всяком
, что при всяком  имеет место неравенство
имеет место неравенство  .
.
Тогда данный ряд можно записать так:

В силу сделанного замечания можно записать ряд
 , который образует геометрическую прогрессию со знаменателем
, который образует геометрическую прогрессию со знаменателем  . Если
. Если  , то
, то  , и прогрессия сходится. Если больший ряд сходится, то будет сходиться и данный ряд. Теорема доказана.
, и прогрессия сходится. Если больший ряд сходится, то будет сходиться и данный ряд. Теорема доказана.
Следствие. Если степенной ряд расходится при значении  , то ряд расходится при всяком значении
, то ряд расходится при всяком значении  , большем по абсолютной величине
, большем по абсолютной величине  ,
,  .
.
Из теоремы Абеля и следствия из этой теоремы вытекает следующее предположение. Для каждого степенного ряда, имеющего как точки сходимости, так и точки расходимости, существует такое положительное число  , что для всех
, что для всех  ,
,  , ряд абсолютно сходится, а для значений
, ряд абсолютно сходится, а для значений  ,
, 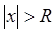 , ряд расходится.
, ряд расходится.
Что касается значений  или
или  , то здесь возможны ситуации, когда ряд сходится в обеих точках, или только в одной из них, или ни в одной.
, то здесь возможны ситуации, когда ряд сходится в обеих точках, или только в одной из них, или ни в одной.
Определение. Число  такое, что для всех
такое, что для всех  ,
,  , степенной ряд сходится, а для всех
, степенной ряд сходится, а для всех  ,
, 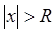 , расходится, называется радиусом сходимости ряда, а интервал
, расходится, называется радиусом сходимости ряда, а интервал  называется интервалом сходимости.
называется интервалом сходимости.
Для ряда  интервал сходимости имеет вид
интервал сходимости имеет вид  с центром в точке
с центром в точке 
 |



Для ряда 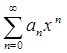 интервал сходимости имеет вид
интервал сходимости имеет вид  с центром в точке
с центром в точке 
 |
-R cx. R x
расх 0 расх
В граничных точках  поведение ряда требует дополнительного исследования.
поведение ряда требует дополнительного исследования.
Можно указать правило для нахождения радиуса сходимости степенного ряда.
Вычисление радиуса сходимости.
Теорема. Если существует предел  , то радиус сходимости ряда равен
, то радиус сходимости ряда равен  , то есть
, то есть  , причем считаем
, причем считаем  , если
, если  , и
, и  , если
, если  .
.
Доказательство.
Предположим, что  , то есть рассмотрим числовой ряд
, то есть рассмотрим числовой ряд  , который является рядом абсолютных величин данного степенного ряда.
, который является рядом абсолютных величин данного степенного ряда.
Тогда  :
:
1. Пусть  - конечное число, отличное от нуля, значит,
- конечное число, отличное от нуля, значит,  . По радикальному признаку Коши ряд, составленный из абсолютных величин ряда, сходится при
. По радикальному признаку Коши ряд, составленный из абсолютных величин ряда, сходится при  , отсюда следует, что
, отсюда следует, что  . При
. При  и
и  ряд расходится для всех значений
ряд расходится для всех значений  .
.
В самом деле, если бы при  ,
, 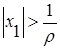 , ряд сходился, то по теореме Абеля для
, ряд сходился, то по теореме Абеля для  , где
, где  , он должен был бы сходиться, чего быть не может. Таким образом, ряд сходится при
, он должен был бы сходиться, чего быть не может. Таким образом, ряд сходится при  и расходится при
и расходится при  и, значит,
и, значит,  .
.
2. Пусть  . Тогда
. Тогда  при всяком значении
при всяком значении  , и ряд сходится для любого
, и ряд сходится для любого  . Значит, ряд абсолютно сходится во всякой точке оси
. Значит, ряд абсолютно сходится во всякой точке оси  и
и  .
.
3. Пусть  . Тогда
. Тогда  при всяком значении
при всяком значении  ,
,  , и значит, ряд не может сходиться ни при каком
, и значит, ряд не может сходиться ни при каком  . На основании теоремы Абеля заключаем, что ряд во всех точках оси
. На основании теоремы Абеля заключаем, что ряд во всех точках оси  (кроме нулевой) расходится и
(кроме нулевой) расходится и  .
.
Теорема. Если 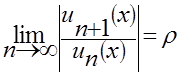 , то радиус сходимости ряда равен
, то радиус сходимости ряда равен  , то есть
, то есть  , причем мы считаем
, причем мы считаем  при
при  и
и  при
при  .
.
Степенные ряды в области сходимости сходятся абсолютно и поэтому можно использовать признаки сходимости рядов с положительными членами.
1. По признаку Даламбера:


Ряд сходится, если  , отсюда радиус сходимости -
, отсюда радиус сходимости -  .
.
2. По интегральному признаку Коши:


Ряд сходится, если  , отсюда следует, что
, отсюда следует, что  .
.
Пример. Найдите область сходимости рядов: 1)  и 2)
и 2)  .
.
1)  .
.
Интервал сходимости 
Исследуем граничные точки.
 расходится;
расходится;
 - сходится условно по признаку
- сходится условно по признаку
Лейбница.
Область сходимости ряда  .
.
2)  , ряд сходится при всех
, ряд сходится при всех  .
.
Свойства степенных рядов.
В силу теоремы Абеля степенной ряд сходится равномерно на  , его можно почленно дифференцировать и интегрировать в интервале сходимости.
, его можно почленно дифференцировать и интегрировать в интервале сходимости.
Теорема. Сумма степенного ряда – это функция, имеющая внутри интервала сходимости производные любого порядка. Эти производные являются суммами степенных рядов, полученных из данного функционального ряда почленным дифференцированием его элементов соответствующее число раз, причем радиус сходимости каждого «производного» ряда тот же, что и у исходного функционального ряда.



Теорема. Сумма степенного ряда есть функция аналитическая в интервале сходимости.
Можно выразить коэффициенты степенного ряда через производные от функции суммы данного ряда

Таким образом, коэффициенты степенного ряда являются соответствующими коэффициентами Тейлора для функции  в точке
в точке  .
.

Если имеется некоторая функция  можно ли ее представить в виде суммы некоторого степенного ряда или, другими словами, можно ли данную функцию разложить в степенной ряд.
можно ли ее представить в виде суммы некоторого степенного ряда или, другими словами, можно ли данную функцию разложить в степенной ряд.
Разложение функций в степенные ряды.
Определение. Функцию  можно разложить в степенной ряд по степеням разности
можно разложить в степенной ряд по степеням разности  , то этот ряд обязательно является рядом Тейлора этой функции.
, то этот ряд обязательно является рядом Тейлора этой функции.

 ,
,
где 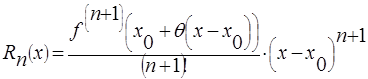 - остаточный член в форме Лагранжа, где
- остаточный член в форме Лагранжа, где  .
.
Необходимым условием разложения функции в ряд Тейлора является дифференцируемость функции бесконечное число раз.
Для того, чтобы ряд Тейлора сходился к данной функции 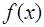 , абсолютные величины всех производных функции
, абсолютные величины всех производных функции  должны быть ограничены одним и тем же числом
должны быть ограничены одним и тем же числом  , где
, где  - постоянная не зависящая от
- постоянная не зависящая от  . Остаточный член
. Остаточный член  определяется неравенством
определяется неравенством  .
.
Разложение элементарных функций в степенные ряды.
1. 

на любом интервале  оси
оси  , значит для всех
, значит для всех  .
.
 (1)
(1)
2. 



 ,
,


……………………………………………

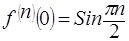 .
.

3. 

4. 
Продифференцируем  и разложим производную по формуле суммы бесконечно убывающей геометрической прогрессии:
и разложим производную по формуле суммы бесконечно убывающей геометрической прогрессии:

Продифференцируем это равенство почленно:
 постоянную интегрирования
постоянную интегрирования  найдем, полагая
найдем, полагая  .
. 

 .
.
5. 
Представим функцию арктангенса в виде интеграла с переменным верхним пределом  . По формуле суммы бесконечно убывающей геометрической прогрессии
. По формуле суммы бесконечно убывающей геометрической прогрессии 



7.  - производное постоянное число.
- производное постоянное число.
 ,
, 
 ,
, 
 ,
, 
………………………………………………………………………
 ,
,
 .
.

 .
.
Область сходимости этого ряда находится по признаку Даламбера:





 .
.