Научный руководитель: Якушенко Татьяна Андреевна, учитель математики

Автор: Якушенко Валентин Александрович

 

МОУ Ярковская средняя общеобразовательная школа, 8 класс

 

Адрес автора: Новосиборская область, Доволенский район, с.Ярки, ул. Ливенская, д.11

тел. 8(383)54-27-295

 

Научный руководитель: Якушенко Татьяна Андреевна, учитель математики

 

Адрес руководителя: Новосиборская область, Доволенский район, с.Ярки, ул. Ливенская, д.11

тел. 8(383)54-27-295

 

Адрес образовательного учреждения: Новосиборская область, Доволенский район, с.Ярки, ул. Ливенская, д.1

тел. 8(383)54-27-248

 

:

с. Ярки, 2010

Оглавление

 

 

I.Введение _________________________________________________стр.3-4

II Основная часть____________________________________________стр.4-10

 

1. Немного о Пифагоре_______________________________________стр.4-5

 

2. Теорема Пифагора ________________________________________стр.5

 

3. Исторические задачи______________________________________стр.5-6

 

4. Теорема Пифагора в

 

· строительстве и архитектуре____________________________стр.6-8

· мобильной связи______________________________________стр.8

· литературе___________________________________________стр.8-10

 

III. Заключение ____________________________________________стр.10-11

 

IV. Литература_____________________________________________стр.11

 

V. Приложение____________________________________________стр.12-16

Приложение №1________________________________________стр.12

Приложение №2________________________________________стр.13

Приложение №3 _______________________________________­­­­­_стр.14

Приложение №4 ________________________________________стр.15

Приложение №5 ________________________________________стр.16

 

 

I. Введение.

В школьном курсе геометрии с помощью теоремы Пифагора решаются только математические задачи. К сожалению, вопрос о практическом применении теоремы Пифагора не рассматривается.

В связи с этим, целью моей работы было выяснить области применения теоремы Пифагора.

В настоящее время всеобщее признание получило то, что успех развития многих областей науки и техники зависит от развития различных направлений математики. Важным условием повышения эффективности производства является широкое внедрение математических методов в технику и народное хозяйство, что предполагает создание новых, эффективных методов качественного и количественного исследования, которые позволяют решать задачи, выдвигаемые практикой.

Рассмотрю примеры практического применения теоремы Пифагора. Не буду пытаться привести все примеры использования теоремы - это вряд ли было бы возможно. Область применения теоремы достаточно обширна и вообще не может быть указана с достаточной полнотой.

Гипотеза:

С помощью теоремы Пифагора можно решать не только математические задачи.

 

По данной исследовательской работе определена следующая цель:

Выяснить области применения теоремы Пифагора.

 

Исходя из вышеназванной цели, были обозначены следующие задачи:

1. Собрать информацию о практическом применении теоремы Пифагора в различных источниках и определить области применения теоремы.
2. Изучить некоторые исторические сведения о Пифагоре и о его теореме.
3. Показать применение теоремы при решении исторических задач.
4. Провести измерения крыши детского садика, решить прикладные задачи по установке ёлки и молниеотвода.
5. Обработать собранные данные по теме.
6. Оформить наработанный материал в виде проекта.

Решению названных задач было посвящено мое исследование, которым я занимался 2 месяца. Я занимался поиском и сбором информации – изучал печатный материал, работал с материалом в интернете, обработкой собранными данными. Решал исторические задачи и занимался задачами по исследованию крыши детского сада, расчетом длины молниеотвода и задачей по установке ёлки. Провел анкетирование учащихся, учителей, родителей и обработал результаты. Было опрошено 27 учащихся 8-11 классов, 14 учителей и 15 родителей учащихся 8 класса (приложение №1). Для своего исследования я вначале изучил вопрос о теореме Пифагора по школьным учебникам «Геометрия 7-9» Атанасяна Л.С. и Руденко В.Н., а также по учебнику Погорелова А.В. «Геометрия 7-11». Рассмотрел в данных учебниках задачи по теореме Пифагора. В Интернете я ознакомился с практическим применением теоремы и историческими задачами. Вопрос о практическом применении теоремы Пифагора и о самом Пифагоре в школьном учебнике геометрии Атанасяна, по которому занимаюсь я, не освещен. Упоминается лишь немного о биографии Пифагора и о том, как древние египтяне строили прямые углы с помощью веревки, разделенной на 12 равных частей (3,4,5). Это же упоминается и в учебнике геометрии Погорелова А.В. А вот в учебнике геометрии Руденко В.Н. по практическому применению теоремы решаются некоторые интересные задачи, хотя вопрос можно сказать, также не освещен. Вопрос о некоторых исторических сведениях, о Пифагоре и его теореме я доработал по книгам Волошинова А.В. «Пифагор» и «Математика и искусство». В книге Литцмана В. «Теорема Пифагора» рассматриваются способы доказательства теоремы.

Исследовав литературные источники, я не нашёл в них вопроса о практическом применении теоремы Пифагора. Поэтому самостоятельно изучить этот вопрос мне удалось только в интернете, где я и выявил некоторые области ее применения.

Меня заинтересовала архитектура с точки зрения применения теоремы Пифагора и я решил провести исследования крыши детского сада «Незабудка», рассмотрел вопрос о возведения молниеотвода на крышу детского сада, а также рассмотрел вопрос об установке новогодней ёлки на площади с. Ярки.

Мне интересно знать, знают ли теорему Пифагора ученики, учителя, родители? И чтобы это выяснить, я провел опрос учеников с 8-11 классы, учителей, родителей.

 

Методика исследования:

1. Изучение теоретического материала.

2. Изучение методик исследования.

3. Практическое выполнение исследования.

4. Коммуникативный (метод измерения, анкетирование).

5. Метод моделирования (модель установки ёлки, молниеотвода).

 

Вид проекта: информационно-исследовательский. Работа выполнялась на занятиях математического кружка, а также я занимался ей в свободное время.

 

 

II. Основная часть

1. Немного о Пифагоре

 

Крепкого телосложения юношу судьи одной из первых в истории Олимпиад не хотели допускать к спортивным состязаниям, так как он не вышел ростом. Но он не только стал участником Олимпиады, но и победил всех противников. Такова легенда. Этот юноша был Пифагор - знаменитый математик. Вся его жизнь – легенда, точнее наслоение многих легенд. Он родился на острове Самос, у берега Малой Азии. Всего 5 километров водной глади отделяло этот остров от большой земли. Совсем юным Пифагор покинул родину. Он прошел по дорогам Египта, 12 лет жил в Вавилоне, где слушал речи жрецов, открывавших перед ним тайны астрономии и астрологии, затем несколько лет – в Италии. Уже в зрелом возрасте Пифагор переселяется в Сицилию и там, в Кротоне, создает удивительную школу, которую назовут пифагорейской. Они были трудолюбивы и аскетичны – Пифагор и его ученики. Вот заповеди пифагорейцев.

• Делай лишь то, что впоследствии не огорчит тебя и не принудит раскаиваться.
• Не делай никогда того, что не знаешь, но научись всему, что следует знать.
• Не пренебрегай здоровьем своего тела.
• Приучайся жить просто и без роскоши.
• Прежде чем лечь спать, проанализируй свой поступки за день.

Трудно сказать, какие научные идеи принадлежали Пифагору, какие – его воспитанникам. Но рассказывают, что Пифагор, доказав свою знаменитую теорему, отблагодарил богов, принеся им в жертву 100 быков.

Пифагор не записал своего учения. Оно известно лишь в пересказах Аристотеля и Платона. Греческий ученый Гераклит утверждал, что Пифагор ученее всех современников, однако порицал его за склонность к магии. Дело в том, что числа для пифагорейцев были наполнены магическим содержанием, они преклонялись перед гармонией чисел.

Пифагор был не только математиком, но и философом. Ему принадлежит немало великих догадок. Вот почему люди помнят его уже две с половиной тысячи лет, а среди знаменитых олимпийских чемпионов Пифагор наиболее знаменит, - ему выпало счастье победить не только соперника, но и время.

2. Теорема Пифагора

Теорема Пифагора доказана более чем 100 способами. Я познакомился с тремя способами доказательства теоремы (Приложение №2) Приведу наиболее простое геометрическое доказательство этой теоремы: площадь квадрата, построенного на гипотенузе прямоугольного треугольника, равна сумме площадей квадратов, построенных на его катетах.

Нарисую два квадрата, стороны которых равны (a+b) – сумме двух катетов (сторон, образующих прямой угол) прямоугольного треугольника (Приложение №3рис. 1). Затем в полученных квадратах выполню построения (Приложение №3рис.2, рис.3).

Все зарисованные на рис.2,3 фигуры – квадраты со сторонами, равными катетам и гипотенузе прямоугольного треугольника. Очевидно, что сумма площадей зарисованных квадратов на рис.2 равна площади зарисованного квадрата на рис.3, а именно площади квадрата со стороной (a+b) за вычетом четырех площадей равных между собой треугольников (Слайд 6).

Итак, теорема Пифагора доказана.

Теорема Пифагора (без доказательства) встречается еще в вавилонских текстах, написанных за 1200 лет до Пифагора. Она была известна в Китае и Индии. Одно из древнейших доказательств теоремы Пифагора, очень громоздкое и трудное, дано Евклидом. О прямоугольном треугольнике со сторонами 3,4,5 единиц длины за 200 лет до н.э. знали и египтяне, считая его магическим.

3. Исторические задачи

Предлагаю несколько исторических задач, найденных в древних источниках.

Задача Бхаскари

( Приложение №3)

«На берегу реки рос тополь одинокий.
Вдруг ветра порыв его ствол надломал.
Бедный тополь упал. И угол прямой
С теченьем реки его ствол составлял.
Запомни теперь, что в этом месте река
В четыре лишь фута была широка
Верхушка склонилась у края реки.
Осталось три фута всего от ствола,
Прошу тебя, скоро теперь мне скажи:
У тополя как велика высота?»

Решение: По теореме Пифагора АВ²= ВС²+АС²;9+16=25, АВ=5 Футов; СD=3+5=8 футов. Ответ: высота тополя 8 футов.

Задача из китайской «Математики в девяти книгах»

(Приложение№3). «Имеется водоем со стороной в 1 чжан = 10 чи. В центре его растет камыш, который выступает над водой на 1 чи. Если потянуть камыш к берегу, то он как раз коснётся его. Спрашивается: какова глубина воды, и какова длина камыша?».

Решение: По теореме Пифагора (x+1)²=x²+25; 2x=24, x=12 чи.; 12+1=13 чи. Ответ: глубина воды-12 чи, длина камыша-13 чи.

Задача из учебника «Арифметика» Леонтия Магницкого

 

«Случися некому человеку к стене лестницу прибрати, стены же тоя высота есть 117 стоп. И обреете лестницу долготью 125 стоп. И ведати хочет, колико стоп сея лестницы нижний конец от стены отстояти имать». Решение: ВС²=АВ²-АС²; ВС²=15625-13689=44 стоп. Ответ: ВС=44 стоп. (Приложение№3).

Задача о бамбуке из древнекитайского трактата "Гоу-гу"

Имеется бамбук высотой в 1 чжан. Вершину его согнули так, что она касается земли на расстоянии 3 чи от корня (1 чжан = 10 чи).Какова высота бамбука после сгибания? Решение: (10-x)²=x²-9; -20x=9-100, -20x=-109, x=109/20 чи.Ответ: x= 4,55 чи. (Приложение№3).

4.Теорема Пифагора в строительстве и архитектуре

Очень легко можно воспроизвести способ построения "натягивателями веревок" прямых углов при помощи прямоугольных треугольников со сторонами 3, 4 и 5. Возьмем веревку длиною в 12 м. и привяжем к ней по цветной полоске на расстоянии 3м. от одного конца и 4 метра от другого. Прямой угол окажется заключенным между сторонами длиной в 3 и 4 метра. ( Приложение №4).

Окно

В зданиях готического и романского стиля верхние части окон расчленяются каменными ребрами, которые не только играют роль орнамента, но и способствуют прочности окон. На рисунке (Приложение №4)представлен простой пример такого окна в готическом стиле. Способ построения его очень прост: из рисунка легко найти центры шести дуг окружностей, радиусы которых равны ширине окна (b) для наружных дуг половине ширины, (b/2) для внутренних дуг. Остается еще полная окружность, касающаяся четырех дуг. Т. к. она заключена между двумя концентрическими окружностями, то ее диаметр равен расстоянию между этими окружностями, т. е. b/2 и, следовательно, радиус равен b/4. А тогда становится ясным и положение ее центра. В рассмотренном примере радиусы находились без всяких затруднений. В других аналогичных примерах могут потребоваться вычисления; покажем, как применяется в таких задачах теорема Пифагора.

В романской архитектуре часто встречается мотив, представленный на рисунке (Приложение №4).Если b по-прежнему обозначает ширину окна, то радиусы полуокружностей будут равны R = b / 2 и r = b / 4. Радиус p внутренней окружности можно вычислить из прямоугольного треугольника, изображенного на рис. пунктиром. Гипотенуза этого треугольника, проходящая через точку касания окружностей, равна b/4+p, один катет равен b/4, а другой b/2-p. По теореме Пифагора имеем: (b/4+p)²=(b/4)²+(b/2-p)²; или b²/16+ bp/2+p²=b²/16+b²/4-bp+p²; откуда bp/2=b²/4-bp. Разделив на b и приводя подобные члены, получим: (3/2)p=b/4, p=b/6.

Строительство крыши

При строительстве домов и коттеджей часто встает вопрос о длине стропил для крыши, если уже изготовлены балки. Например: в доме задумано построить двускатную крышу (форма в сечении). Какой длины должны быть стропила, если изготовлены балки AC=8 м., и AB=BF. (Приложение №4) Решение: Треугольник ADC - равнобедренный AB=BC=4 м., BF=4 м. Если предположить, что FD=1,5 м., тогда из треугольника DBC: DB=2,5 м., из треугольника АВF: АF=√4²+4²=√32≈5,7 м.

Взяв за основу эту задачу, я решил исследовать двускатную крышу детского сада «Незабудка» и проверить, выполняется ли для неё теорема Пифагора. Проведя измерения крыши, получил следующие результаты: длина балки -12,2 м., высота – 3 м., длина стропила – 6,8м. Двускатная крыша в сечении – равнобедренный треугольник, тогда длину стропила вычислю по теореме Пифагора: √6,1²+3² ≈6,8м. Учитывая погрешность измерения, прихожу к выводу, что строители крыши при строительстве крыши пользовались известной теоремой.

Когда я вырасту, и у меня будет своя семья, то я, как настоящий мужчина, обязательно построю дом. Я знаю теперь, что для строительства крыши моего дома обязательно надо применить теорему Пифагора.

При проектировании любых строительных объектов возникает необходимость вычислять стороны прямоугольных треугольников по известным сторонам. Подобные задачи решаются и в нашей повседневной жизни. Например, перед новым годом в центре нашего села Ярки на небольшой площади устанавливается ёлка высотой 5 м. Её всегда устанавливают на прямоугольную призму, сделанную из снега. Ёлка стоит неустойчиво (это проблема) и под воздействием природных явлений (чаще сильного ветра) накреняется, иногда падает. Я предлагаю устанавливать её другим способом. Установить ёлку без снежной призмы высотой 8м. и закрепить её в вертикальном положении. Для этого от вершины ёлки надо сделать проволочные натяжки АВ, АМ, АК одинаковой длины и закрепить на земле на расстоянии 6м от основания елки. Длина натягивающей проволоки должна 10м., т.к. по теореме Пифагора АВ²= АС²+ВС²; АВ= =10 м. (Приложение №5)

А если все-таки высота ёлки 5м., то длину можно рассчитать приближенно. Пусть натягивающую проволоку закрепим на расстоянии 3 м. от основания ёлки, тогда её длина будет равна 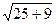= ≈5,8 м.

Молниеотвод

Молниеотвод защищает от молнии все предметы, расстояние до которых от его основания не превышает его удвоенной высоты. Определить оптимальное положение молниеотвода на двускатной крыше, обеспечивающее наименьшую его доступную высоту. Решение: по теореме Пифагора h² ≥ a²+b², значит h ≥ √(a²+b²). Ответ: h ≥√ (a²+b². (Приложение №5)

Гроза и ее непременный атрибут молния – атмосферное явление, таящее в себе достаточно большую опасность. Достаточно сказать, что в год в мире от удара молнии гибнет более 3000 человек (что гораздо больше числа погибших в авиакатастрофах), а материальный ущерб исчисляется миллиардами долларов (в нашей стране - сотнями миллионов рублей). Я считаю, чтовозведение молниеотводов очень актуально для нашего села, т.к. природные катаклизмы не обходят стороной и нас. Так в 2009 году в здание детского сада, во время сильной грозы, «зашла» молния. По предположению заведующей садиком Гельм Т.А. она «зашла» и «вышла» через крышу, повредив электроснабжение. Весь шифер с одной стороны был полностью снесён. К счастью никто не пострадал. На крыше садика молниеотвода нет. Я считаю, что он обязательно должен быть на здании, где находятся дети. Поэтому предлагаю на крыше детского садика восстановить стержневой молниеотвод. Если размеры крыши садика 44м. и 12,2м., то по предыдущей задаче высота молниеотвода должна быть h≥√6,1²+22², h≥22,8м. Так как молниеотвод защищает от молнии все предметы, расстояние до которых от его основания не превышает его удвоенной высоты, то высота молниеотвода должна быть не меньше 11,4 м. По расчетам видно, что высота молниеотвода очень высокая. Можно установить два стержневых молниеотвода, я думаю, это будет экономически выгоднее. Их высоты должны быть не менее 6,3 м., а если учесть ещё и высоту крыши 3 м., то высоты молниеотводов должны быть не менее 3,3 м. (Приложение №5).

· мобильной связи

В настоящее время на рынке мобильной связи идет большая конкуренция среди операторов. Чем надежнее связь, чем больше зона покрытия, тем больше потребителей у оператора. При строительстве вышки (антенны) часто приходится решать задачу какую наибольшую высоту должна иметь антенна, чтобы передачу можно было принимать в определенном радиусе (например, радиусе R=200 км, если известно, что радиус Земли равен 6380 км.?) (Приложение №6). На основе Я на основе задачи, найденной в Интернете, решил решить задачу: какую наименьшую высоту должна иметь вышка мобильной связи, поставленной в селе Утянка, чтобы село Ярки попало в зону связи (расстояние от вышки до Ярков по прямой 10 км.)? Решение: Применив теорему Пифагора, получу уравнение (х+6380)²=10²+6380²; х²+12760х-100=0; D=162817600+400=162818000; 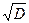≈12760,016; х≈0,008км.

· литературе

Мало кто знает, что Пифагор имел отношение не только к математике, но и к литературе. Он и его теорема воспеты в литературе. О ней писали в своих произведениях римский архитектор и инженер Витрувий, греческий писатель-моралист Плутарх, греческий ученый III в. Диоген Лаэрций, математик V в. Прокл и многие другие.

Существуют много легенд, мифов, рассказов, песен, притчей, небылиц, анекдотов, частушек об этой теореме. Некоторые из них я приведу в своей исследовательской работе (приложения №6, №7). Легенда о том, что в честь своего открытия Пифагор принес в жертву быка или, как рассказывают другие, сто быков, послужила поводом для юмора в рассказах писателей и в стихах поэтов. Так, например, немецкий писатель-романист А. Шамиссо, который в начале XIX в. участвовал в кругосветном путешествии на русском корабле "Рюрик", написал следующие стихи:

Пребудет вечной истина, как скоро
Ее познает слабый человек!
И ныне теорема Пифагора
Верна, как и в его далекий век.
Обильно было жертвоприношенье
Богам от Пифагора. Сто быков
Он отдал на закланье и сожженье.

За света луч, пришедший с облаков.
Поэтому всегда с тех самых пор,
Чуть истина рождается на свет,
Быки ревут, ее почуя, вслед.
Они не в силах свету помешать.
А могут лишь, закрыв глаза, дрожать.

От страха, что вселил в них Пифагор.

 

Теоремой Пифагора и пифагорейской школой восхищается человечество на протяжении всей истории, им посвящают стихи, песни, рисунки, картины. Так художник Ф.А. Бронников (1827-1902) нарисовал картину «Гимн пифагорейцев восходящему солнцу» (Приложение№5).

Картина передает пафос преклонения учеников легендарной школы перед единой гармонией, царящей в мироздании («космосе»), музыке и числе.

 

III Заключение

В результате проведённого исследования я выяснил некоторые области применения теоремы Пифагора. Мной собрано и обработано много материала из литературных источников и интерната по данной теме. Я изучил некоторые исторические сведения о Пифагоре и его теореме, решил ряд исторических задач на применение теоремы Пифагора. Главным в работе считаю предложения по решению выдвинутых мною двух проблем: возведение молниеотвода на крыше детского сада и установке новогодней ёлки на площади села. В результате решения поставленных задач я пришел к выводу, что выдвинутая гипотеза нашла подтверждение. Да, действительно, с помощью теоремы Пифагора можно решать не только математические задачи. Теорема Пифагора нашла своё применение в строительстве и архитектуре, мобильной связи, литературе. А также практическое применение теорема найдёт и при решении тех проблем, которые я обозначил в своей работе и думаю, что администрация нашего села откликнется на мои предложения.

Результатом моей работы является:

1. приобретение навыка работы с литературными источниками;
2. приобретение навыка поиска нужного материала в Интернете;
3. научился работать с большим объёмом информации, отбирать нужную информацию;
4. это мой первый проект по математике, в результате которого я приобрёл опыт обработки данных и написания исследовательского проекта.

Было интересно почувствовать себя исследователем, но главное меня заинтересовал процесс познания. Работа над проектом помогла мне реально применить полученные на уроках знания, навыки, опыт в практической деятельности, в соответствии с моими интересами.

Я предложил заведующей детским садом Гельм Т.А. установить молниеотвод на здании по моим расчетам и вышел к начальнику ЖКХ Горшкову Н.Н. с предложением установить ёлку на следующий год по новой технологии, используя теорему Пифагора.

IV.Литература:

1. Атанасян Л.С. и др. «Геометрия 7-9», М. «Просвещение»,2002, с.383

2. Волошинов А.В. «Математика и искусство», М. «Просвещение», 2000, с.117-119, с.399

3. Волошинов А.В. «Пифагор», М. «Просвещение», 1993,с.223

4. Литцман В. «Теорема Пифагора»,М. «Государственное издательство физико-математической литературы», 1960, с.114

5. Погорелов А.В.«Геометрия 7-11», М.«Просвещение»1992, с.383

6. Руденко В.Н. «Геометрия 7-9», М. «Просвещение»1992,с.383

7. https://encyklopedia.narod.ru/bios/nauka/pifagor/pifagor.html

8. https://moypifagor.narod.ru/use.htm

9. https://moypifagor.narod.ru/literature.htm

V Приложение

Приложение №1

Анкета включала в себя вопросы:

1. Как называется самая известная теорема геометрии?
2. Можете ли вы её сформулировать?

Диаграмма №1 Результаты анкетирования учащихся

 

Диаграмма №2 Результаты анкетирования учителей

 

 

Диаграмма №3 Результаты анкетирования родителей учащихся 8 класса

 

Приложение №2