Описание установки. Вывод рабочей формулы.

ИССЛЕДОВАНИЕ МАЛЫХ ДЕФОРМАЦИЙ ЖЕСТКОУПРУГИХ И ВЯЗКОУПРУГИХ СИСТЕМ. ЗАКОН ГУКА

 

Учебно-методическое пособие к лабораторной работе № 1.2

Владивосток

Исследование малых деформаций жесткоуругих и вязкоупругих систем. Закон Гука.

 

Цель работы: графическим методом исследовать деформацию растяжения жесткоупругой и вязкоупругой систем в области упругой деформации для пружин и резиновой ленты, соответственно.

Задачи: для жесткоупругой системы проверить выполнение закона Гука. С помощью закона Гука рассчитать коэффициенты жесткости данных в работе пружин. Для вязкоупругой системы – резиновой ленты - исследовать механический упругий гистерезис и по графику рассчитать отношение площади под гистерезисом к площади под деформационной кривой нагружения. Показать, что данное отношение пропорционально отношению величины упругой энергии, превращенной в тепловую энергию, к полной упругой энергии, запасенной образцом при деформации.

 

Краткая теория.

Деформация растяжения относится к простейшему виду деформаций. Обобщенной характеристикой деформации растяжения является диаграмма растяжения (рис.1) или график зависимости механического напряжения от относительного удлинения . В диаграмме содержится информация обо всех механических свойствах материала при растяжении. Впервые эта диаграмма была получена Р. Гуком при растяжении металлической проволоки в 1670 г.

Рис. 1. Диаграмма упругой, неупругой и пластической деформации растяжения металлической проволоки

 

Как следует из диаграммы растяжения проволоки, область упругих напряжений имеет два участка, ограниченных пределом пропорциональности и пределом упругости. На первом участке деформационной кривой выполняется закон Гука, устанавливающий линейную зависимость напряжения от относительной деформации , где 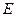- модуль упругости растяжения или модуль Юнга. В настоящее время этот закон Гука в обобщенном виде служит основанием математической теории упругости. А на втором участке соотношение 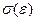нелинейно и закон Гука не выполняется, хотя вплоть до предела упругости тело восстанавливает свои размеры и форму после снятия внешней нагрузки.

Для исследования линейной зависимости и, соответственно, закона Гука хорошей моделью упругого тела является жесткая пружина, для которой предел пропорциональности практически равен пределу упругости (нелинейным участком можно пренебречь). Поэтому важным является практическое использование жесткой пружины в пружинных весах. Взаимосвязь между растяжением пружины и приложенной силой была также впервые исследована Р. Гуком и известна как экспериментальный закон Гука. Достаточно в хорошем приближении можно считать, что сила, требуемая для растяжения пружины, пропорциональна удлинению пружины

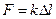(1.1)

где 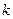- коэффициент жесткости, зависящий от размеров пружины и материала, из которого она изготовлена (рис. 2). При силах, не доходящих до предела упругости, пружина возвращается к своей исходной длине или форме после снятия нагрузки. Под действием внешней силы тело деформируется до тех пор, пока внешняя сила не уравновесится внутренней силой или силой упругости . Переходя к стержню или проволоке заданного материала длиной и площадью поперечного сечения , на которое действует сила , закон Гука можно записать в виде:

, (1.2)

где - механическое напряжение, и перейти к формуле .

 

Рис.2. Зависимость силы растяжения от удлинения пружины.

Под действием внешней приложенной силы в жесткоупругом теле атомы смещаются из своих равновесных положений, что сопровождается увеличением потенциальной энергии тела на величину, равную работе внешней силы. Так средняя сила, требуемая для растяжения пружины, равна

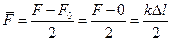, (1.3)

А работа растяжения пружины как мера изменения потенциальной энергии тела при его деформации равна произведению средней силы на удлинение:

, (1.4)

Это означает, что пока удлинение или сжатие пружины пропорционально приложенной силе, отклонения межатомных расстояний от их равновесных значений пропорциональны действующим между атомами силам – силам упругости:

, (1.5)

Таким образом, возвращающие или упругие силы, которые можно получить при дифференцировании потенциальной энергии, согласно условию потенциальности упругих сил , прямо пропорциональны отклонению атомов от положения равновесия. Поэтому тело в области упругих деформаций можно представить как совокупность атомов-шариков, соединенных пружинами, ориентации которых фиксированы другими пружинами.

На втором нелинейном участке деформационной кривой упругой области, лежащей между пределами пропорциональности и упругости, при деформации проявляются вязкоупругие свойства твердых тел. Вязкость или внутреннее трение – это свойство твердых тел (а также газов и жидкостей) оказывать сопротивление деформации. Вязкость твердых тел сопровождается возникновением внутри тела слоев, движущихся относительно друг друга по направлению приложенных сил, и, соответственно, возникновением касательных сил трения между ними. С вязкостью твердых тел связано развитие остаточных деформаций. Однако при очень малых сдвигах внутренних слоев обратный ход деформационной кривой при снятии нагрузки свидетельствует на опыте о восстановлении формы, размеров и объема твердого тела. В этом случае говорят, что данное тело обладает вязкоупругими свойствами. Для таких тел в нелинейной области упругих деформаций наблюдается механический упругий гистерезис, при котором прямой и обратный ход деформационной кривой не совпадают (рис. 3). Механический упругий гистерезис – это проявление внутреннего трения в твердых телах, при котором происходит отставание во времени упругих деформаций от напряжений. Площадь под кривой механического гистерезиса численно определяет ту часть упругой энергии, запасенной телом при деформации, которая превращается во внутреннюю энергию за счет работы сил трения.

Модельным образцом для исследования нелинейного участка упругой области деформационной кривой и наблюдения упругого механического гистерезиса является резиновая лента. Линейный участок деформационной кривой у резиновой ленты как видно на рисунке 3 практически отсутствует или пренебрежимо мал. Кривая упругого гистерезиса называется петлей гистерезиса. Петля упругого гистерезиса может меняться, если образец многократно нагружать и снимать нагрузку, что указывает на связь между явлением внутреннего трения и усталостью материала. Площадь петель гистерезиса при этом увеличивается.

 

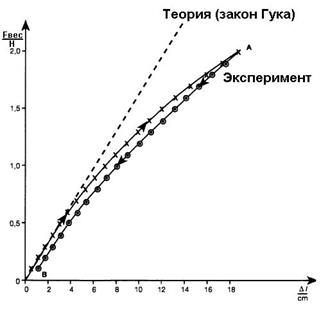
Рис. 3 Зависимость силы растяжения от относительного удлинения резиновой ленты. Петля упругого гистерезиса.

 

Описание установки. Вывод рабочей формулы.

На рисунке 4 показана лабораторная установка. Установка содержит следующее оборудование:

Треножник,

Цилиндрическая опора, вставленная в треножник,

Зажим для образцов на цилиндрической опоре,

Метровая шкала, вставленная в крепежный болт,

Курсоры для шкалы,

Спиральные пружины,

Резиновая лента с квадратным сечением,

Держатель для гирь с отверстиями,

Гири, 10г и гири,50г,

Шелковая нить.

 

Рис. 4. Лабораторная установка

 

Коэффициент жесткости данных в работе пружин определяется из формулы (1.1)

.

 

 

Выполнение работы

1. Подвесьте одну из двух пружин без груза за крепежный болт (рис. 4 и 5).

2. С помощью курсора по шкале линейки снимите отсчет положения нижнего конца пружины , затем подвесьте к пружине держатель массы =10г с грузом массы и снимите отсчет по линейке нового положения нижнего конца пружины , как показано на рис.5. Разность отсчетов 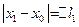, соответствующую удлинению пружины под действием внешней нагрузки, занесите в таблицу 1.

3. Повторите измерения десять раз, пока общая масса грузов не достигнет 200г. Полученные данные измерений занесите в таблицу 1.

4. Повторите опыт по пунктам 2,3 для второй пружины и данные измерений занесите в таблицу 2.

5. По методу случайной ошибки сделайте обработку данных измерения для каждой пружины, получите средние значения коэффициентов жесткости и соответствующие им абсолютные и относительные погрешности для обеих пружин.

 

Рис. 5. Схема измерения абсолютного удлинения пружины

 

6. Постройте графики зависимости растягивающей силы от удлинения для обеих пружин. Рассчитайте по графикам коэффициенты жесткости пружин и сделайте сравнительный анализ результатов, полученных в пунктах 5 и 6.

7. Возьмите резиновую ленту, на обоих концах ее при помощи шелковой нити сделайте маленькие петли как показано на рис.6. Одну из петель пропустите через крепежный болт, а на вторую петлю подвесьте держатель для гирь.

8. Аналогично эксперименту с пружиной подвешивайте к ленте с держателем гирьки с шагом в 10г до тех пор, пока общая масса не достигнет 200г. Полученные значения удлинений на каждом шаге записывайте в таблицу 3. При смене гирек придерживайте рукой ленту.

 

Рис.6. Закрепление резиновой ленты в крепежном блоке

 

9.Снимайте гирьки с держателя также с шагом в 10г. Значения оставшихся удлинений на каждом шаге записывайте в таблицу 3. Последнее измерение должно соответствовать отсчету .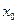

10.Постройте график зависимости растягивающей силы от удлинения резиновой ленты, которая соответствует как увеличению нагружения, так и снятию внешней нагрузки, на миллиметровой бумаге. Определите, какая часть упругой энергии , запасенной при растяжении ленты, затрачивается на внутреннее трение при деформации. Для этого посчитайте на миллиметровой бумаге число целых клеточек и число полуклеточек под кривой нагружения ленты, а затем ту же процедуру повторите для гистерезиса. Отношение суммы целого числа клеточек и деленного пополам числа полуклеточек, соответствующей площади гистерезиса, пропорциональной , к сумме целого числа клеточек и деленного пополам

числа полуклеточек, соответствующей площади под кривой нагружения, пропорциональной запасенной при деформации упругой энергии , даст качественную относительную оценку превращения механической упругой энергии, запасенной при деформации, во внутреннюю энергию в виде тепла . По полученному результату сделайте вывод.

11.Таблицы 1,2 и 3 для внесения в них экспериментальных и расчетных данных начертите самостоятельно.

 

Вопросы к лабораторной работе 1.2 «Исследование малых деформаций жесткоупругих и вязкоупругих систем. Закон Гука»

 

1.Какие деформации твердых тел являются упругими? Какие – неупругими? Какие – пластическими?

2.Определите, что называют диаграммой растяжения? Проведите анализ деформационной кривой и дайте определения всем ее пределам.

3.Сформулируйте физический смысл обобщенного закона Гука и модуля Юнга. От чего зависит модуль Юнга? Запишите размерность модуля Юнга.

4.Объясните схематически, как возникают продольные и поперечные деформации в образце при действии растягивающей силы. Определите физический смысл коэффициента Пуассона. Как коэффициент Пуассона связан с модулем Юнга и модулем сдвига?

5.Сформулируйте закон Гука для деформации пружины. Какой физический смысл имеет коэффициент жесткости пружины? Какова размерность коэффициента жесткости?

6.Определите физический смысл силы упругости. Запишите условие потенциальности упругих сил и нарисуйте модель действия упругих сил в кристалле. Докажите математически линейность закона Гука.

7.Выведите формулу для определения потенциальной энергии упругой деформации.

8.Вчем заключается сущность упругого механического гистерезиса при растяжении полимерных материалов?

9.Какой физический смысл имеет площадь под кривой упругого механического гистерезиса?

10.Как практически можно рассчитать относительную величину, показывающую какую часть от полной упругой энергии, запасенной образцом при деформации, составляет внутренняя энергия, рассеянная в образце.

11.К какому виду фундаментальных взаимодействий относятся силы упругости?

12.Почему для пружин выполняется закон Гука, а для резиновой ленты нет?