ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ «ДОНСКОЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ» (ДГТУ)
Факультет: дорожно-транспортный
Кафедра: Автотранспортные, строительные и дорожные средства
Зав. кафедрой «АСиДС »
В.В. Дерюшев
(подпись)Ф.И.О
«»2018г.
РЕФЕРАТ
на тему: «Вероятность попадания в заданный интервал случайных величин распределенных по нормальному закону»
Автор проекта _______________________.
подпись Ф.И.О
Направление/специальность, профиль/специализация:
23.04.03«Эксплуатация транспортно-технологических машин и комплексов»
код направления наименование направления
профиль «Автосервис» ___________________
наименование профиля
Обозначение реферата Группа АМЭТ21
Руководитель реферата ____________.
(подпись) (должность, Ф.И.О.)
Реферат защищен _____________ ______________ _____________
дата оценка подпись
Ростов-на-Дону
ВВЕДЕНИЕ
Нормальный закон распределения (часто называемый законом Гаусса) играет исключительно важную роль в теории вероятностей и занимает среди других законов распределения особое положение. Это – наиболее часто встречающийся на практике закон распределения. Главная особенность, выделяющая нормальный закон среди других законов, состоит в том, что он является предельным законом, к которому приближаются другие законы распределения при весьма часто встречающихся типичных условиях. Так, к примеру, сумма достаточно большого числа независимых случайных величин, подчиненных каким угодно законам распределения (при соблюдении некоторых весьма нежестких ограничений), приближенно подчиняется нормальному закону. Большинство встречающихся на практике случайных величин, таких, например, как ошибки измерений, ошибки стрельбы и т.д., могут быть представлены как суммы весьма большого числа сравнительно малых слагаемых – элементарных ошибок, каждая из которых вызвана действием отдельной причины, не зависящей от остальных. Каким бы законам распределения ни были подчинены отдельные элементарные ошибки, особенности этих распределений, в сумме большого числа слагаемых нивелируются, и сумма оказывается подчиненной закону, близкому к нормальному.
Вероятность попадания в заданный интервал нормальной случайной величины
Уже известно, что если случайная величина X задана плотностью распределения f (х), то вероятность того, что X примет значение, принадлежащее интервалу (a,b), такова:
P(a<X<b)=

Пусть случайная величина X распределена по нормальному закону. Тогда вероятность того, что X примет значение, принадлежащее интервалу (a,b), равна
P (a< X< b) =

Преобразуем эту формулу так, чтобы можно было пользоваться готовыми таблицами. Введем новую переменную z = (x -- а) /--s. Отсюда x = sz+a, dx = sdz. Найдем новые пределы интегрирования. Если х= a, то z= (a- a) /--s; если х = b, то z = (b- а) /--s.
Таким образом, имеем
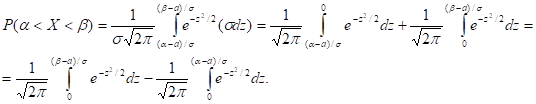
Пользуясь функцией Лапласа
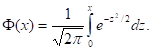
окончательно получим

(*)
Вычисление вероятности заданного отклонения
Часто требуется вычислить вероятность того, что отклонение нормально распределенной случайной величины X по абсолютной величине меньше заданного положительного числа d, т. е. требуется найти вероятность осуществления неравенства | Х -- а |<--d.
Заменим это неравенство равносильным ему двойным неравенством
-- d <Х -- а <--d, или а -- d < X<a+ --d.
Пользуясь формулой (*) (см. § 5), получим

Приняв во внимание равенство
Ф(----d / -- s) = --Ф(d /--s)
(функция Лапласа -- нечетная), окончательно имеем
Р (| X -- а |< d) = 2Ф (d /--s).
В частности, при а = 0
Р (| X |< d) = 2Ф (d /--s).
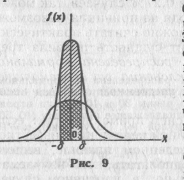
На рис. 9 наглядно показано, что если две случайные величины нормально распределены и а= О, то вероятность принять значение, принадлежащее интервалу (--d,d), больше у той величины, которая имеет меньшее значение s. Этот факт полностью соответствует вероятностному смыслу параметра s (s есть среднее квадратическое отклонение; оно характеризует рассеяние случайной величины вокруг ее математического ожидания).
Замечание. Очевидно, события, состоящие в осуществлении неравенств | X -- а |<d и | Х--а |d, -- противоположные. Поэтому, если вероятность осуществления неравенства | X -- а| < d равна р, то вероятность неравенства | Х--а |d равна 1-- р.
ЗАКЛЮЧЕНИЕ
В работе показаны основные определения и свойства нормального распределения: плотность, функция распределения, связь между нормальными с.в. и стандартными нормальными с.в., подсчитаны начальные и центральные моменты. Указаны значения моды, медианы, асимметрии и эксцесса, характеристические функции и некоторые квантили нормального распределения. Приведены примеры решения некоторых задач, в частности связанных с теоремой Муавра-Лапласа, которая на примере биномиального распределения показывает глубокую связь между нормальным распределением и другими распределениями.