Исторические проблемы физики. Сила, масса, инерциальная система отсчета.
А.И. Сомсиков
Определение силы и массы
В физике смысл каждой вновь вводимой величины, кроме первоначальных, считается выясненным в том случае, когда найдено уравнение, в котором эта величина выражается через ранее введенные, первоначальные же величины не выводимы.
Например, скорость определяется как отношение пройденного пути ко времени, в течение которого путь пройден (путь и время – первоначальные понятия, не поддающиеся дальнейшему разложению); ускорение есть отношение величины изменения скорости ко времени, в течение которого произошло изменение; работа есть произведение силы на пройденный путь; мощность есть отношение работы к промежутку времени, в течение которого она совершалась и т.д.
Не все величины, однако, имеют столь ясно определенный физический смысл и, прежде всего, две фундаментальные величины классической механики - сила и масса.
Причина состоит в том, что Ньютон ввел одновременно обе эти величины в одном уравнении второго закона механики, вследствие чего одна неизвестная величина - сила определялась через другую неизвестную - массу и наоборот.
Логический круг может быть преодолен путем добавления второго уравнения, содержащего те же неизвестные, исключения одной из неизвестных и выражения второй неизвестной через известные.
Недостающее уравнение было также дано Ньютоном (закон всемирного тяготения для неподвижных и медленно движущихся относительно скорости света тел), так что полная система двух уравнений есть:
 ,
,
 .
.
Для того чтобы выяснить физический смысл входящих величин  и
и  , нужно, как сказано, решить эту систему.
, нужно, как сказано, решить эту систему.
Итак, пусть сила, вызывающая ускоренное движение тела с массой  , является силой тяготения:
, является силой тяготения:
 .
.
После сокращения  получим:
получим:  .
.
Откуда:  .
.
Положив теперь 
 , приходим к следующему определению массы:
, приходим к следующему определению массы:  .
.
Массой тела называется произведение ускорения, приобретаемого другим телом, находящимся на заданном расстоянии от него, на квадрат расстояния между телами.
Из формулы видно, что возможно как скалярное, так и векторное истолкование массы:
 .
.
Второй закон механики является феноменологическим определением силы (если положить  ):
):
 .
.
Сила есть произведение ускорений взаимодействующих тел на квадрат расстояния между телами.
Из определения следует, что правильно говорить “сила тел” вместо “сила, приложенная к телу”, т.к. сила не является самостоятельной сущностью, могущей быть приложенной, но лишь указанным выше произведением.
Полная система уравнений ньютоновой динамики состоит из 4-х уравнений:

 ,
,
 ,
,
 ,
,
и содержит 4 неизвестных -  ,
,  ,
,  ,
, 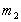 .
.
Решение этой системы есть:
 ,
,
 ,
,
 .
.
Заметим, что отсутствие или изменение любого из приведенных уравнений делает в первом случае невозможным однозначное определение силы и массы, т.к. при этом остается 3 уравнения с 4-мя неизвестными, а во втором равносильно полному изменению смысла  и
и  .
.
А потому, если где-нибудь равенство  , например, заменяется равенством
, например, заменяется равенством  , (
, ( ), то здесь следует начать с того, что неизвестно, что такое
), то здесь следует начать с того, что неизвестно, что такое  и
и  , и то, что обозначено прежней буквой, является совершенно новым понятием.
, и то, что обозначено прежней буквой, является совершенно новым понятием.
Система отсчета
Система отсчета СО, в которой измеряются ускорения  ,
, 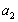 , носит наименование инерциальной системы отсчета (ИСО).
, носит наименование инерциальной системы отсчета (ИСО).
Основным свойством ИСО является независимость ускорения тела 1 от самого этого тела (постоянство массы тела 2 при изменении тела 1), точно так же ускорение тела 2 не зависит от самого тела 2 (постоянство массы тела 1 при изменении тела 2).
Это означает, что в ИСО приращение ускорения с изменением тела 1 относится каждый раз к телу 2, соответственно с изменением тела 2 считается относящимся к телу 1.
Иными словами, с изменением тела 1 ускорение системы отсчета относительно тела 1 не изменяется (система отсчета остается прежней), точно так же с изменением тела 2 ускорение системы отсчета относительно тела 2 не меняется.
Отсюда следует, что для любой пары 1', 2' ИСО остается той же самой, что и для 1, 2.
В самом деле, произвольную пару 1', 2' можно получить из заданной пары 1, 2 путем последовательной замены вначале тела 1 на тело 1', при этом относительно 1' ИСО движется с прежним ускорением  , т.е. не изменяется, а ускорение тела 2 измеряется в этой же системе отсчета; затем тела 2 на тело 2', при этом относительно 2' ИСО движется с прежним ускорением (не изменяется), а ускорение тела 1' измеряется относительно этой же системы отсчета.
, т.е. не изменяется, а ускорение тела 2 измеряется в этой же системе отсчета; затем тела 2 на тело 2', при этом относительно 2' ИСО движется с прежним ускорением (не изменяется), а ускорение тела 1' измеряется относительно этой же системы отсчета.
В итоге, ускорения тел 1', 2' измеряются относительно той же системы отсчета, что и ускорения тел 1, 2, с точностью до любой другой системы, движущейся относительно первой без ускорения.
В ИСО ускорение тела 1 и связанной с ним системы отсчета СО1 равно  , соответственно ускорение тела 2 и системы СО2 -
, соответственно ускорение тела 2 и системы СО2 - 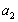 .
.
В СО1 ускорение ИСО равно минус  , а ускорение СО2 равно:
, а ускорение СО2 равно:  .
.
Присоединим к телу 1 некоторое тело 3.
При этом ускорение СО2 в ИСО становится равным  (
( от добавления тела 3 не меняется).
от добавления тела 3 не меняется).
В СО1 ускорение СО2 становится равным  .
.
Таким образом, приращение  от добавления тела 3 в ИСО и в СО1 имеет одинаковую величину и, следовательно, его можно определить измерением в СО1.
от добавления тела 3 в ИСО и в СО1 имеет одинаковую величину и, следовательно, его можно определить измерением в СО1.
Но это приращение в ИСО однозначно определяет массу тела 3!
Заметим, что как только найдена масса хотя бы одного из тел (в данном случае - тела 3), массы всех остальных тел находятся легко, для чего следует последовательно помещать исследуемые тела на заданном расстоянии от тела 3 и измерять ускорение исследуемых тел относительно тела 3.
При этом получим:  ,
,
где  - ускорение i-го тела относительно тела 3,
- ускорение i-го тела относительно тела 3,
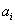 - ускорение i-го тела относительно ИСО,
- ускорение i-го тела относительно ИСО,
 - ускорение тела 3 относительно ИСО.
- ускорение тела 3 относительно ИСО.
Откуда:  ,
,
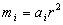 ,
,
где 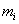 - масса i-го тела.
- масса i-го тела.
Вышесказанное является анализом исторически данного материала.
Правильный порядок построения феноменологической теории динамики следующий.
Начало построения
Геометрическое сравнение тел осуществляется путем сравнения их размеров; в физике тела сравнивают по их движениям,  при этом характеристики движений служат характеристиками тел.
при этом характеристики движений служат характеристиками тел.
Опытным путем установлено, что тела, могущие свободно перемещаться друг относительно друга, самопроизвольно приходят в движение (взаимодействуют), причем в системе отсчета, связанной с телом 1 (СО1) тело 2 приобретает ускорение 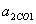 , зависящее от тела 1 (соответственно в СО2 тело 1 имеет ускорение
, зависящее от тела 1 (соответственно в СО2 тело 1 имеет ускорение  , где
, где  ).
).
Однако это ускорение еще не может служить характеристикой тела 1 прежде всего потому, что это величина неоднозначная, а зависит еще и от расстояния: 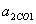 ~
~  .
.
Величиной, не зависящей от расстояния, является произведение:  .
.
Однако и эта величина еще не может служить характеристикой тела 1, т.к. она зависит не только от тела 1, но и от тела 2, иными словами с изменением тела 2 ускорение 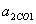 меняется:
меняется:
 .
.
Сделать это ускорение не зависящим от тела 2 можно путем перехода к другой системе отсчета (названной инерциальной СО или ИСО), движущейся ускоренно относительно СО1 (самого тела 1) с некоторым ускорением  .
.
Найти ИСО значит определить  , зная
, зная 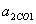 .
.
Пусть даны тело 1 совместно с его системой отсчета СО1 и тело 2.
В СО1 ускорение тела 2 равно 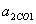 .
.
В искомой ИСО ускорения тел 1, 2 составляют:  ,
,  .
.
При этом:  .
.
Неподвижно присоединим к телу 1 некоторое тело 3.
В искомой ИСО совместное ускорение тел (1 + 3) не зависит от тела 1 и составляет по-прежнему  .
.
Ускорения тела 2 равны теперь: в ИСО - 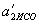 , в СО1 -
, в СО1 - 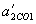 .
.
При этом:  .
.
Пусть:  .
.
Имеем:  , т.е. изменения ускорений тела 2 в СО1 и в ИСО одинаковы, равны
, т.е. изменения ускорений тела 2 в СО1 и в ИСО одинаковы, равны  и могут быть найдены измерениями в СО1.
и могут быть найдены измерениями в СО1.
Уберем теперь тело 1.
В искомой ИСО ускорение оставшегося тела 3 не изменится и составляет по-прежнему  .
.
Ускорения тела 2 равны теперь: в ИСО -  , в СО1 -
, в СО1 -  .
.
При этом:  .
.
Оба ускорения  и
и  изменятся в сравнении с
изменятся в сравнении с  ,
, 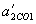 на одинаковую величину, равную
на одинаковую величину, равную  :
:
 ,
,
 .
.
Зная  и
и  , найдем теперь
, найдем теперь  :
:
 .
.
Зная  , найдем
, найдем  :
:
 .
.
При заданном  ускорение
ускорение  теперь уже не зависит от тела 2, а зависит только от тела 1.
теперь уже не зависит от тела 2, а зависит только от тела 1.
В свою очередь произведение  уже не зависит ни от тела 2, ни от расстояния
уже не зависит ни от тела 2, ни от расстояния  и потому может служить однозначной характеристикой тела 1.
и потому может служить однозначной характеристикой тела 1.
Эта характеристика получила наименование массы:
 .
.
Выбор ИСО, не связанной ни с одним из взаимодействующих тел, движущейся ускоренно относительно каждого из тел и притом с разными ускорениями объясняется именно тем, что при этом достигается однозначность характеристик каждого из взаимодействующих тел.
Коэффициенты
Исходные формулы при построении систем единиц динамики Ньютона следующие:  ,
,
 .
.
В системе единиц, предложенной В. Томпсоном, оба коэффициента  принимаются равными единице:
принимаются равными единице:
 ,
,

при этом сам эталон массы оказывается вполне определенным (~ 15 т, при единице длины - см и единице времени - с).
Покажем, как появляются коэффициенты в формулах Ньютона в случае, если эталон массы выбирается произвольно.
Пусть, например, новый эталон массы составляет 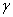 томсоновых эталонов (g имеет произвольное, отличное от единицы числовое значение).
томсоновых эталонов (g имеет произвольное, отличное от единицы числовое значение).
Тогда: 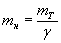 .
.
В системе единиц типа “динамической”  :
:
 .
.
Поскольку:  ,
,  и
и  ,
,  ,
,
то получаем:  или
или  , откуда
, откуда  .
.
В системе единиц типа “гравитационной”  :
:
 .
.
Второй закон Ньютона:  в новой системе единиц:
в новой системе единиц:
 или
или  откуда:
откуда:  .
.
В частном случае, когда коэффициент в точности равен “гравитационной постоянной”, мы получаем собственно гравитационную и собственно динамическую системы единиц.
Если новый эталон массы, измеряемый в долях от томсонова эталона массы, сохраняет прежнюю размерность [см3/c2], то коэффициент есть число, показывающее во сколько раз новый эталон больше или меньше томсонова эталона.
Если же новому эталону дано и новое название (например, грамм), то коэффициент приобретает размерность:
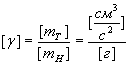 .
.
Итак, гравитационная и динамическая постоянные появляются вследствие произвольности выбора эталона массы при построении систем единиц измерения и не имеют собственного физического смысла.