ВВЕДЕНИЕ
Томография - одно из бурно развивающихся направлений в области получения и обработки информации. Томография позволяет заглянуть внутрь наблюдаемого объекта. Основная проблема томографии - как по получаемым в томографическом эксперименте проекционным данным (например, по рентгеновским снимкам) "увидеть" внутреннюю структуру анализируемого объекта. Область математики, в которой разрабатываются методы решения подобных задач, известна как "интегральная геометрия" [1].
Хронология развития вычислительной томографии:
1895 г. – открытие рентгеновских лучей;
1917 г. – преобразование Радона;
1920 г. – рентгенограмма в медицине;
1930 г. – линейная томография, вращательная томография;
1942 г. – РВТ в радиоастрономии;
1961 г. – сверточный алгоритм;
1964 г. – алгоритм РВТ А. Кормака;
1972 г. – серийный томограф Г. Хаунсфилда;
1977 г. – учебный курс по вычислительной томографии в университете штата Нью-Йорк;
1979 г. – Нобелевская премия А. Кормаку и Г. Хаунсфилду.
1.2 В настоящее время существуют следующие виды томографии:
1) рентгеновская томография;
2) радионуклеидная томография;
3) ЯМР – томография;
4) ультразвуковая томография;
5) оптическая томография;
6) протонно-ионная томография;
7) томография в радиодиапазоне;
8) ЭПР - томография.
Особенно важное значение методы томографии имеют для медицинской диагностики [2].
Все виды томографии по свойствам изучаемых объектов можно разделить на два больших класса: трансмиссионную вычислительную томографию (ТВТ) и эмиссионную вычислительную томографию (ЭВТ). В ТВТ внешнее излучение зондирует пассивный (неизлучающий) объект, частично поглощаясь им. В ЭВТ активный (излучающий) объект представляет собой пространственное распределение источников излучения, при этом выходящее вдоль какого-либо направления излучение является суперпозицией излучений всех источников, лежащих на линии проецирования.
Рассмотрим вначале физический закон распространения внешнего излучения в веществе. Пусть тонкий пучок, например  - излучения, с интенсивностью
- излучения, с интенсивностью  падает на слой вещества с распределением линейного коэффициента поглощения (ослабления)
падает на слой вещества с распределением линейного коэффициента поглощения (ослабления)  вдоль распространения пучка. При этом феноменологически
вдоль распространения пучка. При этом феноменологически  определяют через вероятность
определяют через вероятность  поглощения
поглощения  - кванта при прохождении элементарного пути
- кванта при прохождении элементарного пути  соотношением
соотношением 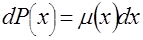 .
.
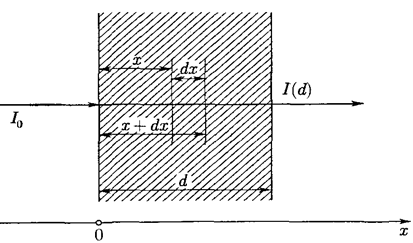 |
 Рисунок 1. К выводу уравнения переноса излучения (1.1).
Рисунок 1. К выводу уравнения переноса излучения (1.1).
Стационарное уравнение переноса излучения в чисто поглощающей неоднородной среде, описывающее процесс излучения в веществе, представляет собой баланс частиц или энергии и имеет вид
 (1.1)
(1.1)
Решением уравнения (2.1) будет закон Бугера-Ламберта-Бэра для неоднородной поглощающей среды, который составляет основу расчетов ТВТ.
 , (1.2)
, (1.2)
где  - интенсивность источника излучения.
- интенсивность источника излучения.
Рассмотрим теперь закон распространения излучения при действии внутренних источников излучения (самоизлучающие объекты).
 |
Рисунок 2. К выводу закона переноса излучения при действии внутреннего источника.
Пусть точечный источник излучает в телесный угол  с интенсивностью
с интенсивностью  в веществе с распределением линейного коэффициента ослабления
в веществе с распределением линейного коэффициента ослабления  вдоль прямой, соединяющей источник с небольшой площадкой
вдоль прямой, соединяющей источник с небольшой площадкой  , наклоненной под углом
, наклоненной под углом  к этой прямой. Тогда для интенсивности
к этой прямой. Тогда для интенсивности  , приходящейся на площадку
, приходящейся на площадку  , получаем [3]
, получаем [3]
 . (1.3)
. (1.3)
Выражение (1.3) учитывает четыре основных фактора: пространственное распределение источника излучения, геометрическое ослабление, ослабление излучения в веществе и наклон площадки детектора. Формула (1.3) лежит в основе ЭВТ.
ПРЕОБРАЗОВАНИЕ РАДОНА
2.1 Рассмотрим задачу восстановления двумерного распределения коэффициента ослабления  при просвечивании объекта излучением внешнего источника. Источник излучения проходит дискретно вдоль объекта. Синхронно с источником с другой стороны объекта движется детектор излучения. Набор отсчетов, полученный таким образом, определяет одномерную функцию, называемую проекцией. Затем система «Источник-детектор» поворачивается относительно объекта на некоторый угол
при просвечивании объекта излучением внешнего источника. Источник излучения проходит дискретно вдоль объекта. Синхронно с источником с другой стороны объекта движется детектор излучения. Набор отсчетов, полученный таким образом, определяет одномерную функцию, называемую проекцией. Затем система «Источник-детектор» поворачивается относительно объекта на некоторый угол 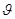 , и снимает новый набор отсчетов, определяющий следующую проекцию. По полученному набору одномерных проекций необходимо восстановить двумерное распределение
, и снимает новый набор отсчетов, определяющий следующую проекцию. По полученному набору одномерных проекций необходимо восстановить двумерное распределение  . Такую схему измерений называют круговой геометрией измерений, а проекции называют параллельными проекциями.
. Такую схему измерений называют круговой геометрией измерений, а проекции называют параллельными проекциями.
 |
Рисунок 3. Схема кругового сканирования с параллельными проекциями.
Пусть на плоскости, где введена прямоугольная система координат  задана функция
задана функция  . Проинтегрируем эту функцию по некоторой прямой, лежащей в данной плоскости. Очевидно, что результат интегрирования, который обозначим
. Проинтегрируем эту функцию по некоторой прямой, лежащей в данной плоскости. Очевидно, что результат интегрирования, который обозначим  , зависит от того, по какой именно прямой проводится интегрирование.
, зависит от того, по какой именно прямой проводится интегрирование.
 |
Рисунок 4. К выводу формул преобразования Радона.
Известно, что всякая прямая может быть описана уравнением
 , (2.1)
, (2.1)
где  - расстояние от начала координат до этой прямой;
- расстояние от начала координат до этой прямой;  - угол, образованный с осью
- угол, образованный с осью  перпендикуляром, опущенным из начала координат на эту прямую.
перпендикуляром, опущенным из начала координат на эту прямую.
Произвольная прямая  однозначно задается двумя параметрами
однозначно задается двумя параметрами  и
и  . Поэтому и результат интегрирования функции
. Поэтому и результат интегрирования функции  по некоторой прямой будет зависеть от этих же параметров, т.е.
по некоторой прямой будет зависеть от этих же параметров, т.е.  . Предположим, что функция
. Предположим, что функция  интегрируется по всевозможным прямым. Подобное интегрирование можно также рассматривать как некоторое преобразование, которое данной функции
интегрируется по всевозможным прямым. Подобное интегрирование можно также рассматривать как некоторое преобразование, которое данной функции  на плоскости
на плоскости  ставит в соответствие функцию
ставит в соответствие функцию  на множестве всех прямых, задаваемую интегралами от
на множестве всех прямых, задаваемую интегралами от  вдоль прямых. Это преобразование называют преобразованием Радона [4,5], а функцию
вдоль прямых. Это преобразование называют преобразованием Радона [4,5], а функцию  часто называют образом функции
часто называют образом функции  в пространстве Радона или проекцией, которая в обозначениях (1.2) имеет вид
в пространстве Радона или проекцией, которая в обозначениях (1.2) имеет вид
 . (2.2)
. (2.2)
Задача ставится следующим образом: функция  неизвестна, но известна функция
неизвестна, но известна функция  , являющаяся образом
, являющаяся образом  в пространстве Радона; требуется по функции
в пространстве Радона; требуется по функции  определить
определить  . Другими словами решение поставленной задачи сводится к отысканию явной формулы обращения или к поиску преобразования, обратного преобразованию Радона. Впервые формула обращения была получена в статье Иоганна Радона, опубликованной в 1917 году в Трудах Саксонской академии наук. Однако эта работа была незаслуженно забыта и формула обращения была открыта заново в 1961 году.
. Другими словами решение поставленной задачи сводится к отысканию явной формулы обращения или к поиску преобразования, обратного преобразованию Радона. Впервые формула обращения была получена в статье Иоганна Радона, опубликованной в 1917 году в Трудах Саксонской академии наук. Однако эта работа была незаслуженно забыта и формула обращения была открыта заново в 1961 году.
Согласно определению радоновского образа и с учетом того, что интеграл от заданной функции вдоль прямой равен интегралу по всей плоскости произведения этой функции на  - функцию, аргументом которой является левая часть уравнения (2.3), имеем [6,7]
- функцию, аргументом которой является левая часть уравнения (2.3), имеем [6,7]
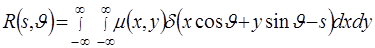 . (2.3)
. (2.3)
Интегрирование, осуществляемое по двум переменным, можно свести к интегрированию по одной переменной. Для этого введем еще одну прямоугольную систему координат  , повернутую относительно
, повернутую относительно  на угол
на угол  . Вспомним, что при переходе от одной из этих систем координат к другой координаты меняются следующим образом:
. Вспомним, что при переходе от одной из этих систем координат к другой координаты меняются следующим образом:

 (2.4)
(2.4)

 (2.5)
(2.5)
Сделаем в (2.3) замену переменных (2.4)
 =
=
=  (2.6)
(2.6)
Для функции  , отличной от нуля в пределах некоторой ограниченной области, ее радоновский образ также определяется выражением (2.3), только интегрирование проводится не по всей плоскости, а задается границами данной области. Так, если
, отличной от нуля в пределах некоторой ограниченной области, ее радоновский образ также определяется выражением (2.3), только интегрирование проводится не по всей плоскости, а задается границами данной области. Так, если  отлична от нуля внутри круга радиуса
отлична от нуля внутри круга радиуса  , то вместо (2.6) имеем
, то вместо (2.6) имеем
 . (2.7)
. (2.7)
В общем случае функция, описывающая радоновский образ, обладает одним важным свойством
 . (2.8)
. (2.8)
Физический смысл этого свойства состоит в том, что любые пары  и
и  согласно (2.1) задают одну и ту же прямую.
согласно (2.1) задают одну и ту же прямую.
Приведем примеры, которые иллюстрируют вычисление радоновских образов.
Пример 1.
Пусть  . Подставим это выражение в (2.6) и получим (см. Приложение А)
. Подставим это выражение в (2.6) и получим (см. Приложение А)
 =
=
=  . (2.9)
. (2.9)
Из (2.9) следует, что если функция  отлична от нуля в точке
отлична от нуля в точке  , то функция, описывающая ее образ в пространстве Радона
, то функция, описывающая ее образ в пространстве Радона  , отлична от нуля на линии
, отлична от нуля на линии
 , (2.10)
, (2.10)
 |
где
 .
.
 |
Рисунок 5.  - функция (а) и ее радоновский образ (б)
- функция (а) и ее радоновский образ (б)
Пример 2.
Пусть  . Подставляя это выражение в (2.6), получим
. Подставляя это выражение в (2.6), получим
 . (2.11)
. (2.11)
 | |||
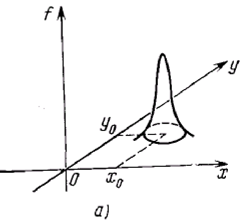 | |||
Рисунок 6. Функция (а) и ее радоновский образ (б)
Область, где  принимает максимальные значения, представляет собой линию, которая определяется выражением (2.10).
принимает максимальные значения, представляет собой линию, которая определяется выражением (2.10).
Пример 3.
При  (2.12)
(2.12)
получаем
 (2.13)
(2.13)
 |  | ||
Рисунок 7. Функция (а) и ее радоновский образ (б)
2.2 В случае самоизлучающего объекта основной задачей ЭВТ является задача восстановления двумерного распределения источников излучения 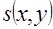 . Для простоты будем считать, что область, в которой распределены источники излучения, целиком расположена в области поглощения излучения, характеризующейся функцией распределения коэффициента ослабления
. Для простоты будем считать, что область, в которой распределены источники излучения, целиком расположена в области поглощения излучения, характеризующейся функцией распределения коэффициента ослабления 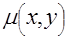 . Обычно при измерениях с помощью ЭВТ, также как и при ТВТ, используют круговую схему с параллельными проекциями.
. Обычно при измерениях с помощью ЭВТ, также как и при ТВТ, используют круговую схему с параллельными проекциями.
 |
Рисунок 8. Круговая геометрия измерений в ЭВТ.
В [3] показано, что для ЭВТ с постоянным коэффициентом ослабления 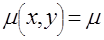 экспоненциальное преобразование Радона в декартовых координатах имеет вид
экспоненциальное преобразование Радона в декартовых координатах имеет вид
 , (2.14)
, (2.14)
а в полярных координатах
 . (2.15)
. (2.15)
Выражение (2.15) можно переписать в другом виде
 . (2.16)
. (2.16)
2.3 Выражения (2.3), (2.6) позволяет по функции  найти ее радоновский образ
найти ее радоновский образ 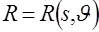 . Существует соотношение, определяющее аналогичную связь между преобразованием Фурье этих функций. Пусть
. Существует соотношение, определяющее аналогичную связь между преобразованием Фурье этих функций. Пусть  - одномерное преобразование Фурье функции
- одномерное преобразование Фурье функции  по переменной
по переменной  , а
, а  - двумерное преобразование Фурье функции
- двумерное преобразование Фурье функции 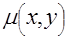 по переменным
по переменным  . Согласно определению
. Согласно определению
 , (2.17)
, (2.17)
 . (2.18)
. (2.18)
В трехмерном пространстве введем прямоугольную систему координат, у которой по одной оси отложены значения  , а по двум другим – значения
, а по двум другим – значения 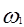 и
и  .
.
 |
Рисунок 9. Центральное сечение двумерного преобразования Фурье
Проведем плоскость, перпендикулярную плоскости  и проходящую через начало координат, такую, что линия ее пересечения с плоскостью
и проходящую через начало координат, такую, что линия ее пересечения с плоскостью  составляет с осью
составляет с осью  угол, равный
угол, равный  (центральное сечение двумерного преобразования Фурье). В сечении этой плоскости со значениями функции
(центральное сечение двумерного преобразования Фурье). В сечении этой плоскости со значениями функции  получается некоторая одномерная функция, зависящая от положения точки на этой прямой, например от ее расстояния до начала координат. Если это расстояние равно
получается некоторая одномерная функция, зависящая от положения точки на этой прямой, например от ее расстояния до начала координат. Если это расстояние равно  , координаты точки этой прямой в плоскости
, координаты точки этой прямой в плоскости  равны
равны  и
и  . Следовательно,
. Следовательно,  подстановкой
подстановкой  ,
,  превращается в
превращается в  .
.
Теорема.
Пусть функция  и ее радоновский образ
и ее радоновский образ  таковы, что существуют их преобразования Фурье. Тогда одномерное преобразование Фурье радоновского образа
таковы, что существуют их преобразования Фурье. Тогда одномерное преобразование Фурье радоновского образа  по переменной
по переменной 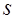 равно функции, описывающей центральное сечение двумерного преобразования Фурье, соответствующее тому значению
равно функции, описывающей центральное сечение двумерного преобразования Фурье, соответствующее тому значению  , при котором вычисляется преобразование Фурье функции
, при котором вычисляется преобразование Фурье функции 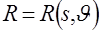
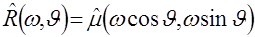 . (2.19)
. (2.19)
Для доказательства (2.19) подставим в (2.17) вместо  выражение (2.6) и сделаем замену переменных, аналогичную (2.4), полагая в (2.4)
выражение (2.6) и сделаем замену переменных, аналогичную (2.4), полагая в (2.4)  . Тогда получаем
. Тогда получаем
 =
=
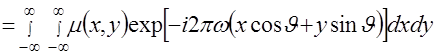 . (2.20)
. (2.20)
Сравнивая последний интеграл в (2.20) с (2.18), видим, что они равны, если в (2.20) под 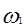 и
и  понимать соответственно
понимать соответственно  и
и  . Следовательно, последний интеграл в (2.20) равен
. Следовательно, последний интеграл в (2.20) равен 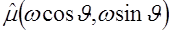 , что и доказывает сформулированную теорему. Легко убедиться, что теорема о центральном сечении справедлива и для случая, когда верно равенство (2.7).
, что и доказывает сформулированную теорему. Легко убедиться, что теорема о центральном сечении справедлива и для случая, когда верно равенство (2.7).
2.4 Рассмотрим теперь формулы обращения и алгоритмы реконструкции, основанные на теореме о центральном сечении. Известно, что по двумерному преобразованию Фурье 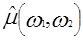 можно найти
можно найти  :
:
 . (2.21)
. (2.21)
Сделаем в (2.21) замену переменных, перейдя в плоскости  к полярным координатам
к полярным координатам  , так что
, так что  ,
,  . Тогда (2.21) принимает вид:
. Тогда (2.21) принимает вид:
 . (2.22)
. (2.22)
Теперь воспользуемся равенством (2.19) и вместо  подставим в (2.22) функцию
подставим в (2.22) функцию  , после чего получим
, после чего получим
 (2.23)
(2.23)
Равенство (2.23) и является искомой формулой обращения, позволяющей с учетом (2.17) по  найти функцию
найти функцию  . Однако привлечение этого равенства для обработки данных томографических экспериментов оказывается не очень удобным из-за используемой в нем области интегрирования. Принимая во внимание равенство
. Однако привлечение этого равенства для обработки данных томографических экспериментов оказывается не очень удобным из-за используемой в нем области интегрирования. Принимая во внимание равенство
 , (2.24)
, (2.24)
получим окончательное выражение для обращения преобразования Радона (см. Приложение Б)
 . (2.25)
. (2.25)
Для выявления детальной структуры алгоритма восстановления перепишем
(2.25) в несколько ином виде. Обозначим
 (2.26)
(2.26)
и введем функцию от  и
и 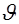 равную
равную
 . (2.27)
. (2.27)
Тогда (2.25) принимает вид
 , (2.28)
, (2.28)
где при вычислении интеграла по 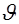 величина
величина  должна быть заменена в соответствии с (2.26) на
должна быть заменена в соответствии с (2.26) на 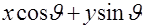 . В целом, алгоритм обращения преобразования Радона можно интерпретировать как последовательность операций:
. В целом, алгоритм обращения преобразования Радона можно интерпретировать как последовательность операций:
1) для данного радоновского образа  определяется его преобразование Фурье
определяется его преобразование Фурье  ;
;
2) функция 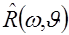 умножается на
умножается на  ;
;
3) вычисляется обратное преобразование Фурье произведения  и тем самым определяется функция
и тем самым определяется функция  ;
;
4) аргументу  функции
функции  присваивается значение (2.26);
присваивается значение (2.26);
5) проводится интегрирование функции  по углу
по углу 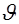 .
.
Рассмотрим теперь иной вид формулы обращения по сравнению с (2.25). Обозначим через  импульсную реакцию фильтра с частотной характеристикой
импульсную реакцию фильтра с частотной характеристикой  . Связь между этими функциями устанавливается прямым и обратным преобразованием Фурье
. Связь между этими функциями устанавливается прямым и обратным преобразованием Фурье
 (2.29)
(2.29)
 (2.30)
(2.30)
Заметим, что функция 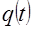 обладает свойством
обладает свойством  .
.
Подставим в (2.25) вместо  правую часть (2.30), а вместо
правую часть (2.30), а вместо  - (2.17). Тогда получим
- (2.17). Тогда получим

 (2.31)
(2.31)
Интегрирование по  дает
дает  , а последующее интегрирование по
, а последующее интегрирование по  приводит к выражению
приводит к выражению
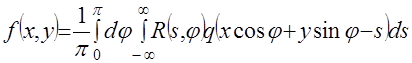 (2.32)
(2.32)
Выражение (2.32) отличается от (2.25) тем, что в последнем участвует преобразование Фурье радоновского образа, а в (2.32) сам радоновский образ. Алгоритм (2.32) можно представить как совокупность трех последовательных операций:
1) вычисляется свертка данного радоновского образа с функцией 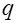 ;
;
2) аргументу  функции
функции  , описывающей получаемую свертку, присваивается значение (2.26);
, описывающей получаемую свертку, присваивается значение (2.26);
3) проводится интегрирование функции  по углу
по углу  .
.
2.5 Обращение экспоненциального преобразования Радона (2.14) – (2.16) представляет существенно более сложную задачу. Ограничимся здесь рассмотрением только случая радиально-симметричной функции  . Тогда экспоненциальное преобразование Радона
. Тогда экспоненциальное преобразование Радона  превращается в экспоненциальное преобразование Абеля
превращается в экспоненциальное преобразование Абеля  [2]
[2]
 =
= 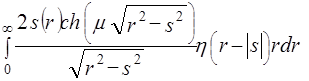 =
=  .
.
В [2] показано, что обратное экспоненциальное преобразование Абеля имеет вид
 =
=
 . (2.33)
. (2.33)
МЕТОД РАЗЛОЖЕНИЯ В РЯД ФУРЬЕ (МЕТОД А. КОРМАКА)
В этом разделе рассмотрим восстановление функции изображения  по ее проекциям, полученным при помощи внешнего источника излучения. Запишем искомую функцию
по ее проекциям, полученным при помощи внешнего источника излучения. Запишем искомую функцию  в полярной системе координат
в полярной системе координат  . Тогда по переменной
. Тогда по переменной  ,
,  , произвольная двумерная функция будет периодической и ее можно разложить в ряд Фурье
, произвольная двумерная функция будет периодической и ее можно разложить в ряд Фурье
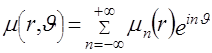 ,
,  . (3.1)
. (3.1)
Аналогично разложим в ряд Фурье по переменной  проекцию
проекцию 
 ,
,  . (3.2)
. (3.2)
В полярной системе координат (2.3) имеет вид
 , (3.3)
, (3.3)
Далее найдем гармонику
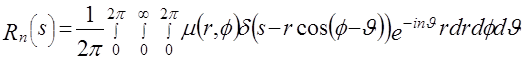 =
=
=  , (3.4)
, (3.4)
где  . Преобразуем функцию
. Преобразуем функцию  , используя свойство
, используя свойство  - функции от сложного аргумента
- функции от сложного аргумента
 ,
,
где  - функция Хевисайда,
- функция Хевисайда, 
 ,
,  . Следовательно,
. Следовательно,
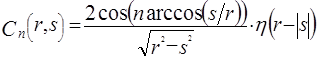 ,
,  =
=
=  (3.5)
(3.5)
где  - многочлен Чебышева 1-го рода порядка
- многочлен Чебышева 1-го рода порядка 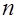 . Выражение (3.5) представляет собой интегральное уравнение относительно неизвестной функции
. Выражение (3.5) представляет собой интегральное уравнение относительно неизвестной функции  . В [3] показано, что решение (3.5) имеет вид:
. В [3] показано, что решение (3.5) имеет вид:
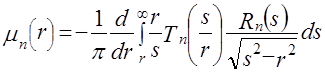 . (3.6)
. (3.6)
Итак, зная проекции  , можно по формуле (3.2) найти гармоники
, можно по формуле (3.2) найти гармоники  , а затем вычислить гармоники
, а затем вычислить гармоники  по формуле (3.6) и, подставляя их в (3.1), найти искомую функцию
по формуле (3.6) и, подставляя их в (3.1), найти искомую функцию  .
.
Для радиально-симметричной функции  в полярной системе координат преобразование Радона
в полярной системе координат преобразование Радона  превращается в частный случай преобразования Абеля
превращается в частный случай преобразования Абеля 
 =
=  =
=
=  . (3.7)
. (3.7)
В [3] показано, что решение интегрального уравнения (3.7) имеет вид
 . (3.8)
. (3.8)