Экспериментальная проверка.
В 1845 году голландский метеоролог из Утрехта, Христофор Хенрик Дидерик Бёйс-Баллот, подтвердил эффект Доплера для звука на железной дороге между Утрехтом и Амстердамом. Локомотив, достигший невероятной на то время скорости 64 км/ч, тянул открытый вагон с группой трубачей. Баллот слушал изменения тона во время движения вагона при приближении и удалении. В тот же год Доплер провел эксперимент, используя две группы трубачей, одна из которых двигалась от станции, а вторая оставалась неподвижной. Он подтвердил, что, когда оркестры играют одну ноту, они находятся в диссонансе. В 1846 году он опубликовал пересмотренную версию своей теории, в которой он рассматривал как движение источника, так и движение наблюдателя. Позднее в 1848 году французский физик Арман Физо обобщил работы Доплера, распространив его теорию и на свет (рассчитал смещение линий в спектрах небесных светил). В 1860 году Эрнст Мах предсказал, что линии поглощения в спектрах звёзд, связанные с самой звездой, должны обнаруживать эффект Доплера, также в этих спектрах существуют линии поглощения земного происхождения, не обнаруживающие эффект Доплера. Первое соответствующее наблюдение удалось провести в 1868 году Уильяму Хаггинсу.
Эффект Доплера для звуковых волн.
Вы могли заметить, что высота звука сирены пожарной машины, движущейся с большой скоростью, резко падает после того, как эта машина пронесется мимо вас. Возможно, вы замечали также изменение высоты сигнала автомобиля, проезжающего на большой скорости мимо вас.
Это связано с тем, что в процессе своего движения автомобиль «догоняет» испущенные ранее волны. Таким образом, наблюдатель у дороги заметит большее число волновых гребней, проходящих мимо него в единицу времени, и, следовательно, для него частота звука будет выше. С другой стороны, волны, распространяющиеся позади автомобиля, будут дальше отстоять друг от друга, поскольку автомобиль как бы «отрывается» от них. Следовательно, за единицу времени мимо наблюдателя, находящегося позади автомобиля, пройдет меньшее количество волновых гребней, и высота звука будет ниже.
Рассмотрим два последовательных гребня волны, причем один из них только что испущен источником звука. Расстояние между этими гребнями равно длине волны λ. Если частота колебаний источника звука равна f, то время, прошедшее между испусканиями волновых гребней, равно Т = 1/f.
Источник звука приближается к наблюдателю.
Источник звука движется со скоростью v ист. За время Т (оно только что было определено) первый гребень волны пройдет расстояние d = vT, где v − скорость звуковой волны в воздухе. За это же время источник звука переместится на расстояние d ист = v ист Т. Тогда расстояние между последовательными гребнями волны, равное новой длине волны λ', запишется в виде
λ' = d – d ист = (v – v ист)T = (v – v ист)/f
поскольку Т= 1/f.
Частота f' волны дается выражением
f’ = v /λ' = v f/(v – v ист),
или
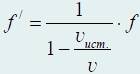
Поскольку знаменатель дроби меньше единицы, мы имеем f’ > f. Например, если источник создает звук на частоте 400 Гц, когда он находится в покое, то, когда источник начинает двигаться в направлении к наблюдателю, стоящему на месте, со скоростью 30 м/с, последний услышит звук на частоте (при температуре 0 °С) 440 Гц.
Источник звука удаляется от наблюдателя.
Новая длина волны для источника, удаляющегося от наблюдателя со скоростью v ист, будет равна
Λ’ = d + d ист.
При этом частота f’ дается выражением
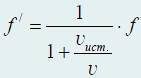
Наблюдатель приближается к источнику звука
Эффект Доплера возникает также в том случае, когда источник звука покоится (относительно среды, в которой распространяются звуковые волны), а наблюдатель движется. Если наблюдатель приближается к источнику звука, то он слышит звук большей высоты, нежели испускаемый источником. Если же наблюдатель удаляется от источника, то звук кажется ему ниже. Количественно изменение частоты здесь мало отличается от случая, когда движется источник, а наблюдатель покоится. В этом случае расстояние между гребнями волны (длина волны λ) не изменяется, а изменяется скорость движения гребней относительно наблюдателя. Если наблюдатель приближается к источнику звука, то скорость волн относительно наблюдателя будет равна v ’ = v + v набл, где v − скорость распространения звука в воздухе (мы предполагаем, что воздух покоится), а v набл − скорость наблюдателя. Следовательно, новая частота будет равна
f = v '/λ = (v + v набл)/λ,
или, поскольку λ = v /f,
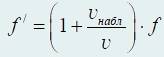
Наблюдатель удаляется от покоящегося источнику звука.
В случае же, когда наблюдатель удаляется от источника звука, относительная скорость будет равна v ’ = v – v набл, и мы имеем
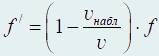
Открытие эффекта Доплера сыграло важную роль в ходе становления современной физики. Одно из подтверждений теории Большого взрыва основывается на этом эффекте. Согласно теории Большого взрыва, Вселенная расширяется. При наблюдении удаленных галактик наблюдается красное смещение – сдвиг спектральных линий в красную сторону спектра. Объясняя красное смещение при помощи эффекта Доплера, можно сделать вывод, согласующийся с теорией: галактики удаляются друг от друга, Вселенная расширяется.