Практическое занятие №3
По теме
Импульс фотона. Световое давление. Эффект Комптона. Корпускулярно-волновой дуализм света.



№ 6.25. Фотон с энергией 0.46 МэВ рассеялся под углом 1200 на покоившемся свободном электроне. Определить относительное изменение частоты фотона.
Дано: e=0,46 МэВ = 7,36×10-14 Дж,
q =1200,
Найти:  .
.
Решение. В задаче рассматривается эффект Комптона: упругое рассеяние коротковолнового электромагнитного излучения на свободных электронах вещества. сопровождающееся увеличением длины волны. Изменение длины волны при этом определяется формулой:
 ,
,
где q - угол рассеяния, 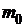 - масса покоя электрона.
- масса покоя электрона.  м - комптоновская длина волны электрона.
м - комптоновская длина волны электрона.
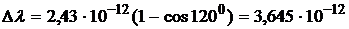 (м).
(м).
Энергия фотона равна
 Þ
Þ 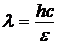 ,
,
вычислим
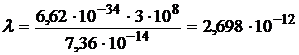 (м)
(м)
- длина волны фотона до рассеяния.
Тогда частота фотона до рассеяния
 (Гц).
(Гц).
После рассеяния частота фотона будет равна
 (Гц)
(Гц)
Вычисляем искомую величину
 .
.
Знак минус означает уменьшение частоты фотона.
Ответ: – 0,575.
551. Красная граница фотоэффекта для цинка l0 = 310 нм. Определить максимальную кинетическую энергию Тmax фотоэлектронов в электрон-вольтах, если на цинк падает свет с длиной волны l= 200 нм.
Дано:
l0 = 31∙10-8 м
l= 2∙10-7 м.
Найти: Тmax-?
Решение. При освещении цинковой пластины светом наблюдается явление фотоэффекта, описываемое уравнением Эйнштейна:
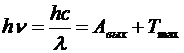 .
.
Здесь Ткин – максимальная кинетическая энергия электронов фототока.
Красная граница фотоэффекта соответствует минимальной энергии фотона, равной работе выхода:
 .
.
Подставим в первое уравнение:
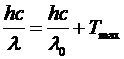 Þ
Þ 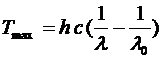 .
.
Вычисляем:
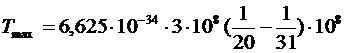 =3,53∙10-19 (Дж)=2,204 (эВ).
=3,53∙10-19 (Дж)=2,204 (эВ).
Ответ: 2,2 эВ.
561. Фотон при эффекте Комптона на свободном электроне был рассеян на угол q=p/2. Определить импульс р (в МэВ/с)*, приобретенный электроном, если энергия фотона до рассеяния была e1 = 1,02 МэВ.
Дано:
q=p/2
 9,11∙10-31 кг - масса покоя электрона
9,11∙10-31 кг - масса покоя электрона
e1 = 1,02 МэВ=
=1,02∙1,6∙10-13 Дж
1 МэВ/с=5,33∙10-32 кг∙м/с
Найти: р -?
Решение. Изменение длины волны фотона при комптоновском рассеянии равно:
 , т.к. по условию q=p/2.
, т.к. по условию q=p/2.
Тогда длина волны фотона увеличилась на 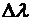 , а его энергия
, а его энергия  уменьшилась на величину
уменьшилась на величину
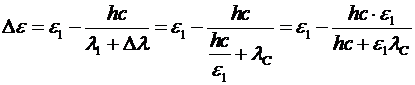 .
.
В соответствии с законом сохранения эта часть энергии e1 фотона перешло к электрону. Т.е. кинетическая энергия электрона будет равна
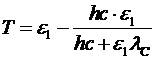 .
.
Вычислим ее:
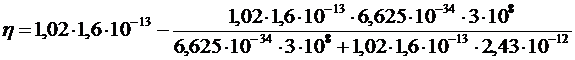 =
=
=1,087∙10-13 (Дж).
Тогда, зная кинетическую энергию электрона, найдем его импульс. Релятивистская формулу связи импульса с кинетической энергией:
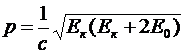 .
.
Вычислим:
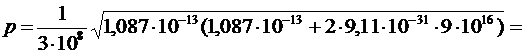
=5,34∙10-22 (кг∙м/с) =
=8,59∙10-9 (МэВ/с).
Ответ: 8,59∙10-9 МэВ/с.
573. Определить коэффициент отражения r поверхности, если при энергетической освещенности Ее = 120 Вт/м2 давление р света на нее оказалось равным 0,5 мкПа.
Дано:
Ее = 120 Вт/м2
р = 5∙10-7 Па
с =3∙108 м/с - скорость света
Найти: r -?
Решение. При нормальном падении света его давление на поверхность вычисляется по формуле:
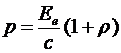 ,
,
где  - энергетическая освещенность поверхности.
- энергетическая освещенность поверхности.
Выражаем искомую величину:
 .
.
Вычислим:
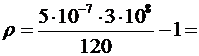 0,25.
0,25.
Ответ: 0,25.
564.Определить максимальное изменение длины волны ∆lmax при комптоновском рассеянии света на свободных электронах и свободных протонах.
Дано:
 9,11∙10-31 кг - масса электрона
9,11∙10-31 кг - масса электрона
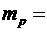 1,6726∙10-27 кг - масса протона
1,6726∙10-27 кг - масса протона
Найти: ∆lmax -?
Решение. В задаче рассматривается эффект Комптона – упругое рассеяние фотонов на свободных частицах вещества (электронах или протонах). В результате передачи части энергии электрону (или протону) энергия фотона уменьшается, а следовательно его длина волны увеличивается. Изменение длины волны фотона при комптоновском рассеянии равно:
 Þ
Þ  .
.
Вычислим:
1) для случая рассеяния на электронах
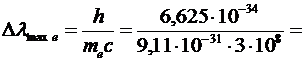 2,424∙10-12 (м),
2,424∙10-12 (м),
2) для случая рассеяния на протонах
 1,32∙10-15 (м).
1,32∙10-15 (м).
Ответ: 2,424∙10-12 м; 1,32∙10-15 м.
574.Давление света, производимое на зеркальную поверхность, р =5 мПа. Определить концентрацию n 0 фотонов вблизи поверхности, если длина волны света, падающего на поверхность, l= 0,5 мкм.
Дано:
r=1
р =5∙10-3 Па
l= 5∙10-7 м.
Найти: n 0 -?
Решение. Для зеркальной поверхности коэффициент отражения r равен единице.
При нормальном падении света его давление на поверхность вычисляется по формуле:
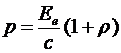 ,
,
где  - энергетическая освещенность поверхности – величина, равная отношению светового потока Ф, падающего на поверхность, к площади S этой поверхности:
- энергетическая освещенность поверхности – величина, равная отношению светового потока Ф, падающего на поверхность, к площади S этой поверхности:
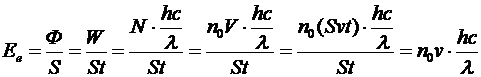 ,
,
где W – энергия падающего излучения, N – число фотонов, «приносящих» энергию, v – скорость движения фотонов, т.е. скорость света. Тогда получаем:
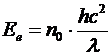 .
.
Подставляем в формулу давления света:
 Þ
Þ
 .
.
Вычислим:
 6,642∙1027 (1/м3).
6,642∙1027 (1/м3).
Ответ: 6,642∙1027 1/м3.
565. Фотон с длиной волны l1= 15 пм рассеялся на свободном электроне. Длина волны рассеянного фотона l2 = 16 пм. Определить угол qрассеяния.
Дано:
l1= 15∙10-12 м
l2= 16∙10-12 м
 =2,43∙10-12 м
=2,43∙10-12 м
Найти: q -?
Решение. В задаче рассматривается эффект Комптона – упругое рассеяние фотонов на свободных частицах вещества (электронах). В результате передачи части энергии электрону (или протону) энергия фотона уменьшается, а следовательно его длина волны увеличивается. Изменение длины волны фотона при комптоновском рассеянии равно:
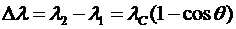 Þ
Þ
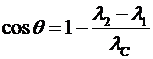 Þ
Þ 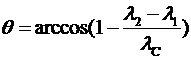 .
.
Вычислим:
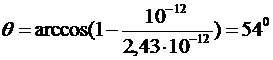 .
.
Ответ: 540.
575. На расстоянии r = 5 м от точечного монохроматического (l = 0,5 мкм) изотропного источника расположена площадка (S = 8 мм2) перпендикулярно падающим пучкам. Определить число N фотонов, ежесекундно падающих на площадку. Мощность излучения Р =100 Вт.
Дано:
r = 5 м
l = 5∙10-7 м
S = 8∙10-6 м2
Р =100 Вт
Найти: N -?
Решение. Мощность излучения – это энергия, которая излучается за 1 с источников во все стороны равномерно. Тогда эта энергия приходится на площадь сферы данного радиуса. А на данную площадку ежесекундно приходится энергия:
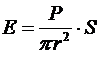 .
.
Считая, что эту энергию приносят фотоны, каждый из которых имеет энергию 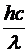 , найдем искомое число фотонов:
, найдем искомое число фотонов:
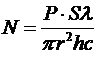 .
.
Вычислим:
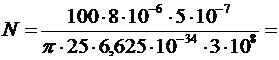 2,563∙1013 (1/с).
2,563∙1013 (1/с).
Ответ: 2,563∙1013 1/с.
556. На металлическую пластину направлен пучок ультрафиолетового излучения (l = 0,25 мкм). Фототок прекращается при минимальной задерживающей разности потенциалов U min=0,96 В. Определить работу выхода А электронов из металла.
Дано:
l = 0,25∙10-6 м
U min=0,96 В
Найти: А -?
Решение. При освещении металлической пластины ультрафиолетом наблюдается явление фотоэффекта, описываемое уравнением Эйнштейна:
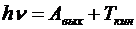 .
.
Здесь Ткин – максимальная кинетическая энергия электронов фототока. Проходя минимальную задерживающую разность потенциалов электроны теряют эту кинетическую энергию, причем в соответствии с законом сохранения энергии:
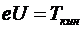 .
.
Энергия фотона связана с его длиной волны соотношением
 .
.
С учетом этого перепишем уравнение Эйнштейна:
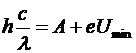 Þ
Þ  .
.
Вычислим:
 6,414∙10-19 (Дж)= 4,0 (эВ).
6,414∙10-19 (Дж)= 4,0 (эВ).
Ответ: 4,0 эВ.
566. Фотон с энергией e1= 0,51 МэВ был рассеян при эффекте Комптона на свободном электроне на угол q = 180°. Определить кинетическую энергию Т электрона отдачи.
Дано:
 =2,43∙10-12 м
=2,43∙10-12 м
e1= 0,51 МэВ
q = 180°
Найти: Т -?
Решение. Изменение длины волны фотона при комптоновском рассеянии на свободном электроне равно:
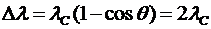 , т.к. по условию q=p.
, т.к. по условию q=p.
Тогда длина волны фотона увеличилась на 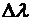 , а его энергия
, а его энергия  уменьшилась на величину
уменьшилась на величину
 .
.
В соответствии с законом сохранения эта часть энергии e1 фотона перешло к электрону. Тогда искомая величина равна
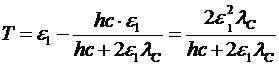 .
.
Вычислим:
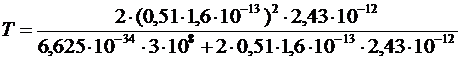 =5,44∙10-14 (Дж) =
=5,44∙10-14 (Дж) =
= 0,34 (МэВ).
Ответ: 0,34 МэВ.
576. На зеркальную поверхность под углом α= 60° к нормали падает пучок монохроматического света (l = 590 нм). Плотность потока энергии светового пучка j=1 кВт/м2. Определить давление р, производимое светом на зеркальную поверхность.
Дано:
α= 60°
r=1
l = 59∙10-8 м
j=1000 Вт/м2
Найти: р -?
Решение. Для зеркальной поверхности коэффициент отражения r равен единице.
При падении света под углом к нормали к поверхности его давление на поверхность вычисляется по формуле:
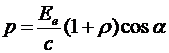 ,
,
где  - энергетическая освещенность поверхности – величина, равная отношению светового потока Ф, падающего на поверхность, к площади S этой поверхности, т.е. по величине она равна плотности потока энергии светового пучка, приходящего на эту поверхность:
- энергетическая освещенность поверхности – величина, равная отношению светового потока Ф, падающего на поверхность, к площади S этой поверхности, т.е. по величине она равна плотности потока энергии светового пучка, приходящего на эту поверхность:
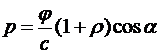 ,
,
Вычислим:
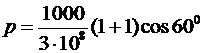 =3,3∙10-6 (Па)=3,3 (мкПа).
=3,3∙10-6 (Па)=3,3 (мкПа).
Ответ: 3,3 мкПа.
568. Определить угол q, на который был рассеян квант с энергией e1 = 1,53 МэВ при эффекте Комптона, если кинетическая энергия электрона отдачи Т=0,51 МэВ.
Дано:
e1 = 1,53 МэВ
 =2,43∙10-12 м
=2,43∙10-12 м
Т=0,51 МэВ
Найти: q -?
Решение. Изменение длины волны фотона при комптоновском рассеянии на свободном электроне равно:
 .
.
Тогда длина волны фотона увеличилась на 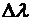 , а его энергия
, а его энергия  уменьшилась на величину
уменьшилась на величину
 .
.
В соответствии с законом сохранения эта часть энергии e1 фотона перешло к электрону. Тогда кинетическая энергия электрона отдачи равна
 .
.
Выражаем отсюда искомый угол рассеяния:
 Þ
Þ  ,
,
 ,
,
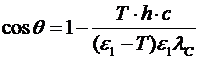 Þ
Þ 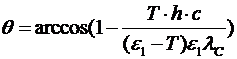 .
.
Вычислим:
 =33,60.
=33,60.
Ответ: 33,60.
578. Свет с длиной волны l= 600 нм нормально падает на зеркальную поверхность и производит на нее давление р=4 мкПа. Определить число N фотонов, падающих за время t=10 с на площадь S= 1 мм2 этой поверхности.
Дано:
l= 6∙10-7 м
р=4∙10-6 Па
t=10 с
S= 10-6 м2
Найти: N -?
Решение. Для зеркальной поверхности коэффициент отражения r равен единице.
При нормальном падении света его давление на поверхность вычисляется по формуле:
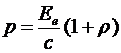 ,
,
где  - энергетическая освещенность поверхности – величина, равная отношению светового потока Ф, падающего на поверхность, к площади S этой поверхности:
- энергетическая освещенность поверхности – величина, равная отношению светового потока Ф, падающего на поверхность, к площади S этой поверхности:
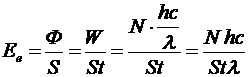 ,
,
где W – энергия падающего излучения, N – число фотонов, падающих на поверхность за время t.
Подставим в формулу давления:
 Þ
Þ  .
.
Вычислим:
 =1,811∙1016 .
=1,811∙1016 .
Ответ: 1,811∙1016.
569.Фотон с энергией e1 = 0,51 МэВ при рассеянии на свободном электроне потерял половину своей энергии. Определить угол рассеяния q.
Дано:
e1 = 0,51 МэВ=
=0,51∙1,6∙10-13 Дж
n=2
 =2,43∙10-12 м
=2,43∙10-12 м
Найти: q -?
Решение. В задаче рассматривается эффект Комптона – упругое рассеяние фотонов на свободных частицах вещества (электронах). В результате передачи части энергии электрону энергия фотона уменьшается, а следовательно его длина волны увеличивается. Изменение длины волны фотона при комптоновском рассеянии равно:
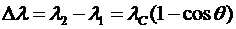 .
.
Энергия фотона через длину волны выражается так:
 Þ
Þ  ,
,
отсюда следует, что при уменьшении энергии фотона в 2 раза, т.к. по условию потеряна половина энергии, длина волны увеличивается в 2 раза, т.е.  .
.
Получаем:
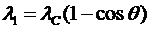 ,
,
 Þ
Þ 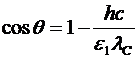 .
.
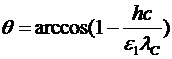 .
.
Вычислим:
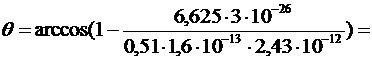 890.
890.
Ответ: 890.
579. На зеркальную поверхность площадью S = 6 см2 падает нормально поток излучения Фе = 0,8 Вт. Определить давление р и силу давления F света на эту поверхность.
Дано:
S = 6∙10-4 м2
Фе = 0,8 Вт
r =1
Найти: р -? F -?
Решение. Для зеркальной поверхности коэффициент отражения r равен единице.
При нормальном падении света его давление на поверхность вычисляется по формуле:
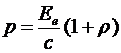 ,
,
где  - энергетическая освещенность поверхности – величина, равная отношению светового потока Ф е, падающего на поверхность, к площади S этой поверхности:
- энергетическая освещенность поверхности – величина, равная отношению светового потока Ф е, падающего на поверхность, к площади S этой поверхности:
 ,
,
тогда
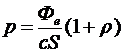 .
.
По определению давление равно отношению силы давления к площади поверхности:
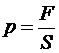 Þ
Þ 
Вычислим:
 =8,9∙10-6 (Па) = 8,9 (мкПа),
=8,9∙10-6 (Па) = 8,9 (мкПа),
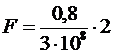 =0,53∙10-8=5,3∙10-9 (Н).
=0,53∙10-8=5,3∙10-9 (Н).
Ответ: 8,9 мкПа; 5,3 нН.
№ 570. Определить импульс ре электрона отдачи, если фотон с энергией e1 = 1,53 МэВ в результате рассеяния на свободном электроне потерял 1/3 своей энергии.
Дано:
e1 = 1,53 МэВ=
=1,53∙1,6∙10-13 Дж=
=2,45∙10-13 Дж
k=1/3
Найти: ре -?
Решение. Считаем, что до столкновения электрон покоился. Тогда после столкновения кинетическая энергия электрона отдачи согласно закону сохранения энергии равна:
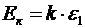 =0,816∙10-13 Дж,
=0,816∙10-13 Дж,
т.е энергию, которую потерял фотон. приобрел электрон отдачи.
Зная кинетическую энергию электрона, найдем его импульс. Поскольку кинетическая энергия электрона сравнима с его энергией покоя:
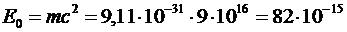 Дж=0,82∙10-13 Дж,
Дж=0,82∙10-13 Дж,
то используем релятивистскую формулу связи импульса с кинетической энергией:
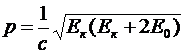 .
.
Вычислим:
 4,72∙10-22 (кг∙м/с).
4,72∙10-22 (кг∙м/с).
Ответ: 4,72∙10-22 кг∙м/с.
№ 580. Точечный источник монохроматического (l= 1 нм) излучения находится в центре сферической зачерненной колбы радиусом R= 10 см. Определить световое давление р, производимое на внутреннюю поверхность колбы, если мощность источника Р= 1 кВт.
Дано:
l= 10-9 м
R =0,1 м
Р= 103 Вт
r=0
Найти: р -?
Решение. Для зачерненной поверхности коэффициент отражения r равен нулю.
При нормальном падении света его давление на поверхность вычисляется по формуле:
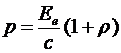 ,
,
где  - энергетическая освещенность поверхности – величина, равная отношению светового потока Ф, падающего на поверхность, к площади S этой поверхности:
- энергетическая освещенность поверхности – величина, равная отношению светового потока Ф, падающего на поверхность, к площади S этой поверхности:
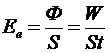 ,
,
где W – энергия падающего излучения.
Так как источник света находится внутри колбы, то его мощность равна световому потоку. Площадь сферической поверхности колбы равна
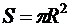 .
.
Подставляем:
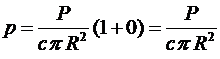 .
.
Вычислим:
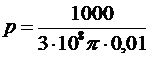 =1,061∙10-4 (Па).
=1,061∙10-4 (Па).
Ответ: 0,106 мПа.
Задачи для самостоятельного решения:
