10-7
| Криволинейное движение . | ||||
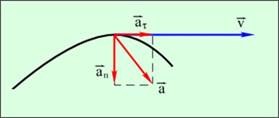
| При криволинейном движении вектор скорости всегда направлен по касательной к траектории движения. Любое криволинейное движение можно представить в виде суммы прямолинейных движений и движений по окружностям разных радиусов. Скорость изменяется как по величине, так и по направлению. Вектор ускорения направлен под углом к вектору скорости. |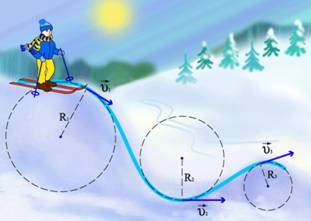 
| |||
| РАВНОМЕРНОЕ ДВИЖЕНИЕ ТОЧКИ ПО ОКРУЖНОСТИ. | ||||
Равномерное движение точки по окружности- движение точки с постоянной по модулю скоростью (v=const) по траектории, представляющей собой окружность.
Но, т.к. скорость всегда направлена по касательной к траектории движения, то по направлению она изменяется.
Значит равномерное движение по окружности – ускоренное движение!
Точка совершает перемещение с постоянной по модулю скоростью, следовательно:
 .
В этом случае скорость точки называется линейной скоростью (l – длина дуги).
Вектор линейной скорости направлен по касательной к окружности в данной точке.
| 
| |||
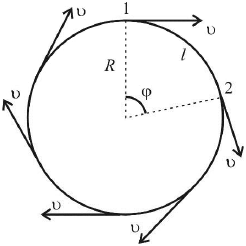
Можно характеризовать изменение положения тела с помощью углового перемещения (угла поворота) j.
Возьмем несколько концентрических окружностей и построим для всех центральный угол j так, чтобы радиусы этих окружностей, образующие угол, накладывались друг на друга. Из рисунка видно, что одному и тому же углу j соответствуют у одной окружности дуга l и радиус r, а у другой – дуга L и радиус R. За меру угла можно принять отношение длины дуги к радиусу:  .
Единица измерения угла в этом случае наз. радианом (сокращение – рад).
1 радиан — центральный угол, длина дуги которого равна радиусу окружности.
| 
| |||
Если точка совершила полный оборот, то длина дуги равна длине окружности.
Следовательно:  - полный оборот точки соответствует 2p радиан.
Для перевода единиц составим пропорцию:  . Следовательно: 
| ||||
Равномерное движение точки по окружности – это движение, при котором точка за любые равные промежутки времени совершает одинаковые угловые перемещения (поворачивается на одинаковые углы).
Если характеризовать движение углом поворота, то удобно ввести
угловую скорость: 
- угловая скорость показывает, на какой угол поворачивается точка при равномерном движении по окружности за единицу времени.
Единица измерения в СИ - 1 рад/с.
| ||||
Можно сказать, что равномерным движением по окружности наз. движение с постоянной угловой скоростью. Линейная и угловая скорости связаны между собой:
 , т.е. 
| ||||
К важным характеристикам вращательного движения относятся частота и период. Период - физическая величина, показывающая, чему равно время, за которое точка совершает один полный оборот.
Если обозначить N – число оборотов, а Т – период, то:  .
Единица измерения в СИ – 1 с.
Т.к. за период точка поворачивается на угол 2p, то  .
Частота – количество оборотов, которое совершила точка за единицу времени:
 .
Единица измерения в СИ – 1 Гц (герц).
Частота равна одному герцу, если за 1 секунду точка совершает один полный оборот (1Гц=1с-1). Частота и период – взаимно обратные величины:  .
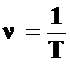Следовательно:  .
| ||||
| Центростремительное ускорение. | ||||
| При движении по окружности с постоянной по модулю скоростью она постоянно изменяется по направлению. Характеристикой этого изменения является центростремительное или нормальное ускорение. Ускорение нормально, т.е. перпендикулярно скорости в любой момент времени. | 
| |||
| В ектор ускорения при равномерном движении по окружности направлен к центру окружности (центру вращения). Поэтому ускорение называется центростремительным ускорением. |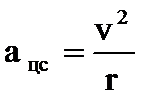 
| |||
Центростремительное ускорение показывает изменение скороститолько по направлению, но не меняет по величине.
Используя связь между угловой и линейной скоростями, получим:
| ||||
| 
| 
| ||
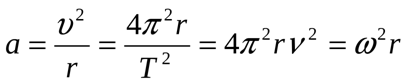
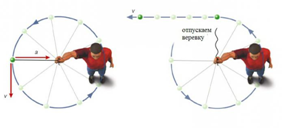
При прекращении действия цетростремительной силы тело будет двигаться по прямой:
| ||||