Раздел 5. Предикаты. Исчисление предикатов
5.1.1 Недостаточность логики высказываний. Средствами логики высказываний удается описать и анализировать далеко не всякие рассуждения. В первую очередь это касается рассуждений, правильность которых основана на связи между элементами внутренней структуры элементарных высказываний, которая логикой высказываний не учитывается. Но они могут быть описаны на языке логики предикатов, которая является расширением логики высказываний, то есть вместе со всеми понятиями логики высказываний содержит ряд других понятий.
5.1.2 Предикаты и способы их задания. Рассмотрим высказывательную форму « ». Каждому значению переменной х на множестве действительных чисел эта форма ставит в соответствие высказывание и тем самым одно из значений истинности (элемент множества
». Каждому значению переменной х на множестве действительных чисел эта форма ставит в соответствие высказывание и тем самым одно из значений истинности (элемент множества  ). Так, значению х, равному 0, соответствует истинное высказывание
). Так, значению х, равному 0, соответствует истинное высказывание  ; при
; при  получаем ложное высказывание
получаем ложное высказывание  ; при
; при  снова получаем истинное высказывание
снова получаем истинное высказывание  . Вообще, всякому значению х, кратному
. Вообще, всякому значению х, кратному  , соответствует истинное высказывание, а всем остальным значениям х соответствуют ложные высказывания.
, соответствует истинное высказывание, а всем остальным значениям х соответствуют ложные высказывания.
Таким образом, данная высказывательная форма задает отображение множества R действительных чисел на множество  , иначе говоря, задает функцию с областью определения R и множеством значений
, иначе говоря, задает функцию с областью определения R и множеством значений  .
.
Функция, задаваемая на R высказывательной формой  , всюду принимает значение 1.
, всюду принимает значение 1.
Высказывательная форма  на любом числовом множестве задает функцию с единственным значением 0.
на любом числовом множестве задает функцию с единственным значением 0.
Определение: Функция, все значения которой принадлежат множеству  , называется предикатом.
, называется предикатом.
Предикаты, как правило, обозначают буквами P, Q, R или  ,
, 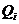 ,
, 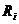 , где
, где  – натуральное число. Под символом
– натуральное число. Под символом  понимают значение предиката Р, соответствующее элементу а из его области определения.
понимают значение предиката Р, соответствующее элементу а из его области определения.
Чаще всего предикаты задают высказывательными формами. Однако существуют и другие способы задания предикатов. Так, например, таблица
| а | б | в | г | д |
задает предикат на множестве 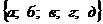 . Табличный способ задания пригоден только для предикатов, область определения которых – конечное множество.
. Табличный способ задания пригоден только для предикатов, область определения которых – конечное множество.
Пусть, например, даны высказывательные формы: 1)  ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4)  . Положим для определенности, что все переменные в этих формах принимают значения из множества R действительных чисел. Форма 1) содержит одну переменную и называется одноместной; форма 2) содержит две переменные х и у и называется двуместной; формы 3) и 4) будут называться трехместными. Вообще форму с п различными переменными называют п-местной формой. Высказывание считается нуль-местной высказывательной формой. Различные переменные могут принимать значения из разных множеств, либо из одного и того же множества независимо друг от друга. Одинаковые переменные в одной и той же форму имеют одно и то же множество значений и одновременно принимают одинаковые значения.
. Положим для определенности, что все переменные в этих формах принимают значения из множества R действительных чисел. Форма 1) содержит одну переменную и называется одноместной; форма 2) содержит две переменные х и у и называется двуместной; формы 3) и 4) будут называться трехместными. Вообще форму с п различными переменными называют п-местной формой. Высказывание считается нуль-местной высказывательной формой. Различные переменные могут принимать значения из разных множеств, либо из одного и того же множества независимо друг от друга. Одинаковые переменные в одной и той же форму имеют одно и то же множество значений и одновременно принимают одинаковые значения.
Для дальнейшего удобно принять следующее соглашение: если высказывательная форма, не содержащая знаков логических операций, при каком-нибудь наборе входящих в нее переменных теряет смысл, то будем считать, что этому набору соответствует значение 0.
Одноместная высказывательная форма задает предикат на множестве значений входящей в нее переменной.
Пример 5.1. Если переменная х в высказывательной форме «Река х впадает в Каспийское море» принимает значения из множества М названий рек, то эта форма задает предикат Р с областью определения М.
Пример 5.2. Если переменные в высказывательных формах 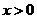 и
и  принимают значения из одного и того же числового множества, например, из множества R. Тогда эти формы задают на R один и тот же предикат
принимают значения из одного и того же числового множества, например, из множества R. Тогда эти формы задают на R один и тот же предикат  .
.
Пример 5.3. Высказывательная форма  задает на R предикат
задает на R предикат  , причем
, причем  .
.
Для рассмотрения вопроса о задании высказывательными формами п -местных предикатов (при  ) нам понадобятся понятия «упорядоченная п -ка» и «декартово произведение множеств».
) нам понадобятся понятия «упорядоченная п -ка» и «декартово произведение множеств».
Будем называть упорядоченной п-кой («энкой») совокупность п не обязательно различных объектов вместе с заданным порядком их расположения. Если  , то п -ка называется парой; если
, то п -ка называется парой; если 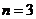 , то тройкой и так далее. Объекты, составляющие п -ку, называют ее компонентами. Будем записывать упорядоченную п -ку с помощью круглых скобок, внутри которых компоненты п -ки располагаются в заданном порядке. Две упорядоченные п -ки считаются равными, если их компоненты и порядок их расположения совпадают. Например,
, то тройкой и так далее. Объекты, составляющие п -ку, называют ее компонентами. Будем записывать упорядоченную п -ку с помощью круглых скобок, внутри которых компоненты п -ки располагаются в заданном порядке. Две упорядоченные п -ки считаются равными, если их компоненты и порядок их расположения совпадают. Например,  и
и  – различные упорядоченные пары;
– различные упорядоченные пары;  и
и  – различные упорядоченные тройки.
– различные упорядоченные тройки.
Для описания игры в шахматы каждой клетке шахматной доски ставится в соответствие пара, первая компонента которой есть элемент множества  , а вторая – элемент множества
, а вторая – элемент множества  . Множество таких пар называется декартовым произведением множеств
. Множество таких пар называется декартовым произведением множеств  и
и  (взятых именно в таком порядке).
(взятых именно в таком порядке).
Вообще, декартовым произведением 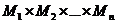 непустых множеств
непустых множеств  ,
,  , …,
, …,  называется множество всевозможных упорядоченных п-ок, первая компонента каждой из которых принадлежит
называется множество всевозможных упорядоченных п-ок, первая компонента каждой из которых принадлежит  , вторая –
, вторая –  и так далее, а последняя принадлежит
и так далее, а последняя принадлежит  .
.
Для декартова произведения п различных множеств М введем сокращенное обозначение  : при
: при 
 , при
, при 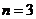
 .
.
Рассмотрим двуместную высказывательную форму  . Пусть х принимает значения из множества
. Пусть х принимает значения из множества  , а у – из множества
, а у – из множества  . Эта форма задает два предиката
. Эта форма задает два предиката  и
и  соответственно на множествах
соответственно на множествах  и
и  .
.

| 
| 
| 
| 
| 
|
| (1; 2) | 1 < 2 | (2; 1) | 1 < 2 | ||
| (1; 4) | 1 < 4 | (2; 2) | 2 < 2 | ||
| (2; 2) | 2 < 2 | (2; 3) | 3 < 2 | ||
| (2; 4) | 2 < 4 | (4; 1) | 1 < 4 | ||
| (3; 2) | 3 < 2 | (4; 2) | 2 < 4 | ||
| (3; 4) | 3 < 4 | (4; 3) | 3 < 4 |
Таким образом, двуместная высказывательная форма определяет, вообще говоря, два различных предиката.
Для того чтобы с помощью высказывательной формы с более чем одной переменной задать предикат однозначно, достаточно выбрать и указать для переменных какой-либо порядок. Если для переменных высказывательной формы  выбран порядок
выбран порядок  и
и  – соответственно множества значений переменных
– соответственно множества значений переменных  , то эта форма задает предикат на множестве
, то эта форма задает предикат на множестве  .
.
Условимся, говоря «предикат, заданный высказывательной формой Ф» и не указывая при этом порядка переменных, полагать, что для переменных принят алфавитный порядок либо порядок возрастания их номеров. Иногда для краткости будем говорить просто «предикат Ф», например, «предикат  » (подразумевается алфавитный порядок переменных) или «предикат
» (подразумевается алфавитный порядок переменных) или «предикат  » (считаем, что переменные упорядочены по возрастанию номеров).
» (считаем, что переменные упорядочены по возрастанию номеров).
Предикат, заданный на множестве упорядоченных п -ок, называется п -местным. При п, равном 1, 2, 3, имеем соответственно одноместный, двуместный, трехместный предикаты.
Остановимся на происхождении термина «предикат» и на эволюции его значения. На латыни слово «предикат» (praedicatum) означает «сказуемое». Традиционная логика выделяет в элементарном высказывании (суждении) субъект и предикат. Субъект (логическое подлежащее) – то, о чем говорится в высказывании; предикат (логическое сказуемое) – то, что говорится (утверждается или отрицается) о субъекте. Например, в высказывании «Кошка имеет четыре ноги» «кошка» – субъект, «имеет четыре ноги» – предикат. Если вместо слова «кошка» поставить слово «собака», то снова получится истинное высказывание «Собака имеет четыре ноги». Если же в качестве субъекта взять слово «курица», то получится ложное высказывание «Курица имеет четыре ноги». Заменив субъект переменной, получим высказывательную форму «Х имеет четыре ноги» и предикат как функцию, задаваемую этой формой. Естественным обобщением понятия «одноместный предикат» является понятие «п -местный предикат».
Одноместные предикаты иногда называют предикатами-свойствами, а п -местные при n > 1 – предикатами-отношениями. Так, например, предикат  выражает свойство чисел (быть отрицательным числом), а предикат
выражает свойство чисел (быть отрицательным числом), а предикат  – отношение между числами (быть меньше).
– отношение между числами (быть меньше).
5.1.3 Множество истинности предиката. Каждому предикату Р, заданному на множестве М, соответствует подмножество этого множества, состоящее из тех и только тех элементов М, которым соответствует значение 1 предиката Р. Это подмножество М называется множеством истинности предиката Р. Множество истинности предиката Р обозначают 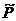 . Заметим, что
. Заметим, что  .
.
Пример 5.4. Предикат Р задан высказывательной формой «Река Х впадает в Каспийское море» на множестве М названий всевозможных рек. Здесь  .
.
Пример 5.5. Предикат  задан высказывательной формой
задан высказывательной формой  , переменные которой принимают значения из множества
, переменные которой принимают значения из множества 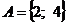 . Областью определения предиката
. Областью определения предиката  является множество
является множество  . Составим таблицу для предиката
. Составим таблицу для предиката  :
:

| 
| 
|
| (2; 2) | 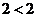
| |
| (2; 4) | 
| |
| (4; 2) | 
| |
| (4; 4) | 
|
Из таблицы видно, что 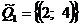 . Приняв для переменных обратный порядок, получим предикат
. Приняв для переменных обратный порядок, получим предикат  , для которого
, для которого  .
.
Пример 5.6. Для предикатов Р и Q, заданных на R высказывательными формами  и
и  , соответственно имеем
, соответственно имеем  ,
,  .
.
Если множество истинности предиката совпадает с его областью определения, то такой предикат называется тождественно истинным. Если множество истинности предиката пусто, то такой предикат называется тождественно ложным.
Два предиката с одной и той же областью определения различны тогда и только тогда, когда их множества истинности не совпадают.
5.1.4 Равносильность высказывательных форм. Пусть в высказывательных формах Ф1 и Ф2 одинаковые переменные принимают одни и те же значения из одного и того же множества. Такие высказывательные формы называются равносильными, если при всяком наборе значений входящих в них переменных они принимают одинаковые значения истинности.
Утверждение о равносильности высказывательных форм Ф1 и Ф2 записывают так:  .
.
Пример 5.7. Пусть переменные в перечисленных примерах принимают значения из R.
1.  , так как обе формы становятся истинными высказываниями при
, так как обе формы становятся истинными высказываниями при  и ложными – при всех других значениях х.
и ложными – при всех других значениях х.
2.  ; обе формы становятс2я истинными высказываниями тогда и только тогда, когда х принимает значения из множества
; обе формы становятс2я истинными высказываниями тогда и только тогда, когда х принимает значения из множества  .
.
3. 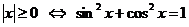 , так как обе формы истинны при любом значении переменной х.
, так как обе формы истинны при любом значении переменной х.
4.  ; обе формы ложны при любом значении х.
; обе формы ложны при любом значении х.
5.  ; обе формы истинны при
; обе формы истинны при 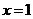 и любом значении у и ложны при
и любом значении у и ложны при  .
.
6. Формы 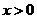 и
и  не равносильны; форма
не равносильны; форма 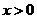 истинна при положительных значениях х и любых значениях у, а форма
истинна при положительных значениях х и любых значениях у, а форма  истинна только при положительных значениях у.
истинна только при положительных значениях у.
7. Формы  и
и  не равносильны; при
не равносильны; при  форма
форма  истинна, а
истинна, а  ложна.
ложна.
Если в качестве множества значений переменной для форм  и
и  взять любое подмножество R, не содержащее 0 (например,
взять любое подмножество R, не содержащее 0 (например, 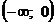 ), то эти формы окажутся равносильными. Таким образом, истинность высказывания
), то эти формы окажутся равносильными. Таким образом, истинность высказывания 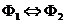 зависит, вообще говоря, от множества значений переменных, входящих в эти формы.
зависит, вообще говоря, от множества значений переменных, входящих в эти формы.
Отношение равносильности высказывательных форм рефлексивно, симметрично и, при условии, что одинаковые переменные принимают значения из одного и того же множества, транзитивно.
Замену формы  равносильной ей формой
равносильной ей формой  называют равносильным преобразованием формы
называют равносильным преобразованием формы  .
.
5.1.5 Логические операции и операции над множествами. Выясним связь между логическими операциями над высказывательными формами и операциями над множествами истинности предикатов, определяемыми этими формами.
Отрицанием высказывательной формы Ф называется высказывательная форма, ложная при тех наборах значений переменных, которые обращают Ф в истинное высказывание, и истинная при тех наборах значений переменных, которые обращают Ф в ложное высказывание. Отрицание высказывательной формы Ф обозначается  .
.
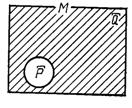 Пример 5.8. (переменная принимает значения из R). 1.
Пример 5.8. (переменная принимает значения из R). 1.  . 2. Высказывательные формы
. 2. Высказывательные формы  и
и  не равносильны, так как при
не равносильны, так как при  форма
форма  истинна, а форма
истинна, а форма  ложна (см. п. 5.1.2).
ложна (см. п. 5.1.2).
Теорема 1. Если предикаты P и Q заданы на М соответственно высказывательными формами  и
и  , то
, то  (рис.).
(рис.).
Конъюнкцией высказывательных форм  и
и  называется высказывательная форма, истинная при тех и только тех значениях входящих в нее переменных, которые обращают обе формы
называется высказывательная форма, истинная при тех и только тех значениях входящих в нее переменных, которые обращают обе формы  и
и  в истинные высказывания. Конъюнкция высказывательных форм
в истинные высказывания. Конъюнкция высказывательных форм  и
и  обозначается
обозначается  .
.
Пример 5.9. (переменные принимают значения из R). 1.  . 2.
. 2.  . 3.
. 3.  .
.
Теорема 2. Если предикаты  ,
,  и
и  заданы на М соответственно высказывательными формами
заданы на М соответственно высказывательными формами 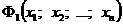 ,
,  и
и  , то
, то  .
.
Из школьного курса алгебры известно, что множество решений системы (то есть конъюнкции) уравнений или неравенств есть пересечение множеств решений входящих в нее уравнений или неравенств. При этом: 1) во всех высказывательных формах, составляющих систему, подразумевается один и тот же (как правило, алфавитный) порядок переменных; 2) если высказывательные формы, образующие систему, содержат не одни и те же переменные, то (явно или неявно) вводятся так называемые «фиктивные» переменные с нулевыми коэффициентами так, чтобы множества переменных во всех предложениях совпали. Например, система уравнений  рассматривается как система
рассматривается как система  ; иначе множество её решений нельзя было бы рассматривать как пересечение множеств решений составляющих уравнений. В самом деле, множество
; иначе множество её решений нельзя было бы рассматривать как пересечение множеств решений составляющих уравнений. В самом деле, множество  решений первого уравнения есть
решений первого уравнения есть  , а каждый элемент множества
, а каждый элемент множества  решений второго уравнения – это пара чисел, то есть
решений второго уравнения – это пара чисел, то есть  , тогда как множество решений данной системы имеет вид
, тогда как множество решений данной системы имеет вид  .
.
Дизъюнкцией высказывательных форм  и
и  называется высказывательная форма, ложная при тех и только тех наборах значений входящих в неё переменных, которые обращают обе формы
называется высказывательная форма, ложная при тех и только тех наборах значений входящих в неё переменных, которые обращают обе формы  и
и  в ложные высказывания. Дизъюнкция высказывательных форм
в ложные высказывания. Дизъюнкция высказывательных форм  и
и  обозначается
обозначается  .
.
Пример 5.10. (переменные принимают значения из R). 1.  . 2.
. 2.  , так как при
, так как при  форма
форма  обращается в ложное высказывание, а форма
обращается в ложное высказывание, а форма  – в истинное высказывание.
– в истинное высказывание.
Теорема 3. Если предикаты  ,
,  и
и  заданы на М соответственно высказывательными формами
заданы на М соответственно высказывательными формами 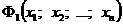 ,
,  и
и 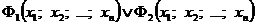 , то
, то  .
.
Все сказанное выше о системах уравнений (неравенств) относится и к совокупностям (дизъюнкциям) уравнений (неравенств) с той разницей, что множество решений совокупности уравнений (неравенств) есть объединение множеств решений входящих в неё уравнений (неравенств).
Импликацией высказывательных форм  и
и  называется высказывательная форма, ложная при тех и только тех наборах значений входящих в неё переменных, которые обращают
называется высказывательная форма, ложная при тех и только тех наборах значений входящих в неё переменных, которые обращают  в истинное высказывание, а
в истинное высказывание, а  – в ложное высказывание. Импликация высказывательных форм
– в ложное высказывание. Импликация высказывательных форм  и
и  обозначается
обозначается  .
.
Пример 5.11. 1. Импликация «х – простое число, следовательно, х – нечетное число» ложна только при  . 2. Импликация
. 2. Импликация  ложна только при отрицательных значениях х и у. 3. Импликация
ложна только при отрицательных значениях х и у. 3. Импликация  истинна при всех действительных значениях х. (При
истинна при всех действительных значениях х. (При  действует соглашение, принятое в п. 5.1.2.) 4. Импликация
действует соглашение, принятое в п. 5.1.2.) 4. Импликация 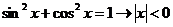 ложна при любых значениях переменных.
ложна при любых значениях переменных.
Эквиваленцией высказывательных форм  и
и  называется высказывательная форма, которая становится истинным высказыванием, если формы
называется высказывательная форма, которая становится истинным высказыванием, если формы  и
и  обе становятся истинными либо ложными высказываниями; если же одна из форм
обе становятся истинными либо ложными высказываниями; если же одна из форм  и
и  становится истинным высказыванием, а другая ложным, то их эквиваленция становится ложным высказыванием. Эквиваленция высказывательных форм
становится истинным высказыванием, а другая ложным, то их эквиваленция становится ложным высказыванием. Эквиваленция высказывательных форм  и
и  обозначается
обозначается  .
.
Пример 5.12. 1. Эквиваленция  истинна при любых значениях переменных. 2. Эквиваленция
истинна при любых значениях переменных. 2. Эквиваленция 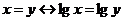 ложна, когда переменные х и у принимают равные неположительные значения; при всех остальных значениях переменных эта эквиваленция истинна. Например, при
ложна, когда переменные х и у принимают равные неположительные значения; при всех остальных значениях переменных эта эквиваленция истинна. Например, при 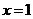 ,
, 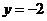 формы
формы  и
и  обращаются в ложные высказывания (соглашение п. 5.1.2); следовательно, форма
обращаются в ложные высказывания (соглашение п. 5.1.2); следовательно, форма 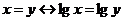 становится истинным высказыванием. 3. Эквиваленция
становится истинным высказыванием. 3. Эквиваленция  ложна при всех значениях переменной.
ложна при всех значениях переменной.
5.1.6 Следование и включение. Говорят, что высказывательная форма Ф2 следует из высказывательной формы Ф1, если  обращается в истинное высказывание при любых наборах значений входящих в нее переменных.
обращается в истинное высказывание при любых наборах значений входящих в нее переменных.
Утверждение «Из Ф1 следует Ф2» кратко будем записывать так:  .
.
Поскольку импликация  обращается в ложное высказывание только в тех случаях, когда Ф1 обращается в истинное высказывание, а Ф2 – в ложное, данное определение можно переформулировать так: из Ф1 следует Ф2, если всякий раз, когда Ф1 становится истинным высказыванием, Ф2 также становится истинным высказыванием.
обращается в ложное высказывание только в тех случаях, когда Ф1 обращается в истинное высказывание, а Ф2 – в ложное, данное определение можно переформулировать так: из Ф1 следует Ф2, если всякий раз, когда Ф1 становится истинным высказыванием, Ф2 также становится истинным высказыванием.
Пример 5.13 (в пунктах 1-5  )
)
1. Из равенства  следует равенство
следует равенство  .
.
2. Из равенства  не следует равенство
не следует равенство  , так как при
, так как при 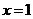 первое равенство верно, а второе – неверно.
первое равенство верно, а второе – неверно.
3. Из равенства  следует неравенство
следует неравенство  , так как корни 0 и 1 уравнения являются решениями неравенства.
, так как корни 0 и 1 уравнения являются решениями неравенства.
4. Из неравенства  следует любая высказывательная форма Ф, так как это неравенство не выполняется ни при каком значении переменной, и поэтому форма
следует любая высказывательная форма Ф, так как это неравенство не выполняется ни при каком значении переменной, и поэтому форма  истинна при любых значениях входящих в нее переменных.
истинна при любых значениях входящих в нее переменных.
5. Форма  следует из любой формы Ф, так как неравенство
следует из любой формы Ф, так как неравенство  верно при любых значениях х, и поэтому форма
верно при любых значениях х, и поэтому форма  истинна при любых значениях входящих в нее переменных.
истинна при любых значениях входящих в нее переменных.
6. Из формы «x – сын y и z » следует форма «y и z – родители x », но из формы «y и z – родители х » не следует форма «х – сын y и z », так как существует набор значений переменных (дочь, отец, мать), при которых форма «y и z – родители х » становится истинным высказыванием, а форма «х – сын y и z » – ложным высказыванием.
7. Из формы «х четно» не следует форма «х кратно 3», если  и следует, если
и следует, если  . В самом деле, на последнем множестве всякий раз, когда истинна первая форма, истинна и вторая.
. В самом деле, на последнем множестве всякий раз, когда истинна первая форма, истинна и вторая.
Из последнего примера видно, что наличие отношения следования (так же как и отношения равносильности) между высказывательными формами зависит, вообще говоря, от множества, на котором они рассматриваются. В отличие от следования и равносильности в логике высказываний, где переменные обозначают произвольные элементарные высказывания, здесь идет речь о предложениях с переменными, заменяющими какой-либо член предложения (чаще всего подлежащее или дополнение). С каждой переменной связывается множество ее значений – чисел или каких-либо других объектов (предметов). Переменные такого рода называются предметными (напомним, что переменные для высказываний мы называли высказывательными или истинностными).
Отношение следования между высказывательными формами с предметными переменными связано с отношением включения между множествами истинности предикатов, определяемых этими формами.
Теорема 4. Если высказывательные формы 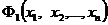 и
и  определяют предикаты
определяют предикаты  и
и  , то
, то  тогда и только тогда, когда
тогда и только тогда, когда  .
.
Свойства и отношения
5.2.1 Свойства как одноместные предикаты. Пусть дано непустое множество  . Всякая одноместная высказывательная форма Ф с переменной, принимающей значения из
. Всякая одноместная высказывательная форма Ф с переменной, принимающей значения из  , выражает свойство, присущее некоторым элементам множества
, выражает свойство, присущее некоторым элементам множества  . Множество М таких элементов есть подмножество
. Множество М таких элементов есть подмножество  ; в частности, оно может совпадать с
; в частности, оно может совпадать с  либо быть пустым. Например, высказывательная форма «х – простое число» выделяет из множества
либо быть пустым. Например, высказывательная форма «х – простое число» выделяет из множества  его подмножество
его подмножество 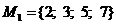 , из множества
, из множества  – подмножество
– подмножество  , из множества
, из множества  – подмножество
– подмножество  . Заменив переменную х любой другой переменной, мы, очевидно, выразим то же самое свойство; все эти формы определяют на множестве
. Заменив переменную х любой другой переменной, мы, очевидно, выразим то же самое свойство; все эти формы определяют на множестве  один и тот же предикат, поэтому свойство элементов множества можно рассматривать как одноместный предикат, заданный на этом множестве. Так как предикат полностью определен, если задано его множество истинности, то понятие «свойство элементов данного множества» можно свести к понятию «подмножество элементов данного множества». Множество элементов, обладающих свойством Р, называют объемом данного свойства. Приняв такую точку зрения, мы должны будем считать одинаковыми любые два «равнообъемных» свойства, например такие два свойства элементов множества параллелограммов, как свойства быть ромбом с прямым углом или прямоугольником с равными смежными сторонами.
один и тот же предикат, поэтому свойство элементов множества можно рассматривать как одноместный предикат, заданный на этом множестве. Так как предикат полностью определен, если задано его множество истинности, то понятие «свойство элементов данного множества» можно свести к понятию «подмножество элементов данного множества». Множество элементов, обладающих свойством Р, называют объемом данного свойства. Приняв такую точку зрения, мы должны будем считать одинаковыми любые два «равнообъемных» свойства, например такие два свойства элементов множества параллелограммов, как свойства быть ромбом с прямым углом или прямоугольником с равными смежными сторонами.
5.2.2 Классификация. Пусть на множестве  задано свойство Р, то есть так или иначе выделено подмножество
задано свойство Р, то есть так или иначе выделено подмножество 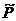 множества
множества  ; тогда имеем разбиение
; тогда имеем разбиение  на два подмножества:
на два подмножества: 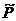 и
и  . Такое разбиение называется классификацией множества
. Такое разбиение называется классификацией множества  по основанию Р.
по основанию Р.
Пусть задано множество  однозначных натуральных чисел:
однозначных натуральных чисел:  . Классифицируем его по основанию «быть простым числом»(рис.).
. Классифицируем его по основанию «быть простым числом»(рис.).

 | |||||
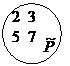 | |||||
 | |||||
Если предикат Р задать высказывательной формой Р (х) = «х – простое число», то эта классификация описывается формой 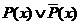 .
.
Зададим на множестве  еще одно свойство
еще одно свойство  . Тогда получим разбиение множества
. Тогда получим разбиение множества  на четыре подмножества (рис.), причем некоторые из них могут быть пустыми.
на четыре подмножества (рис.), причем некоторые из них могут быть пустыми.

Такое разбиение есть классификация элементов множества  по основаниям Р и
по основаниям Р и  . Эту классификацию можно описать следующим образом:
. Эту классификацию можно описать следующим образом:

Если  означает свойство «быть четным числом», то элементы множества
означает свойство «быть четным числом», то элементы множества  однозначных натуральных чисел окажутся расклассифицированы на: а) простые четные
однозначных натуральных чисел окажутся расклассифицированы на: а) простые четные 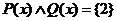 ; б) простые нечетные
; б) простые нечетные  ; в) четные и непростые
; в) четные и непростые  ; г) нечетные и непростые
; г) нечетные и непростые  .
.
Если на множестве  заданы три свойства Р, Q и R, то имеем разбиение множества
заданы три свойства Р, Q и R, то имеем разбиение множества  на восемь подмножеств (рис.).
на восемь подмножеств (рис.).

Это разбиение есть классификация множества  по трем основаниям Р, Q и R, которая описывается высказывательной формой:
по трем основаниям Р, Q и R, которая описывается высказывательной формой:

 .
.
Аналогично проводится классификация по любому числу оснований. Классификация элементов множества  по п основаниям есть разбиение этого множества на
по п основаниям есть разбиение этого множества на  подмножеств (некоторые из них могут оказаться пустыми).
подмножеств (некоторые из них могут оказаться пустыми).
Очевидно, что при правильной классификации: 1) пересечение двух любых классов пусто; 2) объединение всех классов равно множеству, элементы которого классифицируются.
Эти два условия называют правилами классификации; невыполнение хотя бы одного из них свидетельствует о том, что классификация произведена неправильно.
5.2.3 Отношения как одноместные предикаты. Равенство, неравенство, параллельность, перпендикулярность, подобие, следование, равносильность, а также дружба, родство, соседство – все это примеры отношений. Понятие «отношение» можно уточнить с помощью понятия «предикат».
Пример 5.14.
1. Высказывательная форма « » выделяет из множества пар прямых на плоскост
» выделяет из множества пар прямых на плоскост