Определение динамической нагрузки на подшипники

Министерство образования Республики Беларусь

 

 

Учреждение образования

«МОГИЛЕВСКИЙ ГОСУДАРСТВЕННЫЙ

УНИВЕРСИТЕТ ПРОДОВОЛЬСТВИЯ»

 

 

Кафедра прикладной механики

 

Т Е О Р Е Т И Ч Е С К А Я М Е Х А Н И К А

 

Примеры решения задач расчетно-графических, контрольных
и самостоятельных работ для студентов специальностей
1-36 09 01 «Машины и аппараты пищевых производств» и
1-36 20 01 «Низкотемпературная техника» специализации
1-36 20 01 01 «Холодильные машины и установки»
дневного и заочного обучения

 

Могилев 2007

 

 

УДК 531(076)

 

Рассмотрены и рекомендованы к изданию кафедрой ПМ
Протокол № 1 от 30 августа 200 7 г.

 

 

Составитель к.т.н., доцент А.Я.Протас

 

 

Рецензент к.т.н., доцент Б.И.Игнатов

 

 

Протас А.Я. Теоретическая механика. Примеры решения задач
расчетно-графических, контрольных и самостоятельных работ для студентов
специальностей 1-36 09 01 «Машины и аппараты пищевых производств» и
1-36 20 01 «Низкотемпературная техника» специализации «Холодильные машины и установки» дневного и заочного обучения. – Могилев: УО МГУП, 2007. – 43с.

 

 

Настоящее пособие включает примеры решения задач контрольных,
расчетно-графических работ по курсу и может использоваться также при
самостоятельном (дистанционном) освоении теоретической механики. Включены примеры по основным темам статики, кинематики и динамики, приведены схемы, расчеты и даны пояснения. Электронный вариант может использоваться через Интернет.

Рис. 39, библ. 3 названия.

 

© Протас Анатолий Яковлевич, 2007

 

© УО «Могилевский государственный университет продовольствия», 2007

 

 

 

С о д е р ж а н и е

 

ВВЕДЕНИЕ……………….………………………………………………….4

СТАТИКА

1. Задача С1…………………………………………………………………..5

2. Задача С2…………………………………………………………………..6

3. Задача С3…………………………………………………………………..8

4. Задача С4………………………………………………………………....10

КИНЕМАТИКА

5. Задача К1……………………………………………………………...….12

6. Задача К2……………………………………………………………...….13

7. Задача К3……………………………………………………………...….15

8. Задача К4………………………………………………………………....17

ДИНАМИКА

9. Задача Д1………………………………………………………………....20

10. Задача Д2……………………………………………………………...….22

11. Задача Д3……………………………………………………………...….24

12. Задача Д4………………………………………………………………....26

13. Задача Д5……………………………………………………………...….29

14. Задача Д6………………………………………………………………....34

15. Задача Д7………………………………………………………………....35

16. Задача Д8………………………………………………………………....38

 

СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ……………………....42

 

 

 

ВВЕДЕНИЕ

 

Настоящая разработка предназначена, прежде всего, для студентов заочного обучения, но с успехом может использоваться студентами стационара и даже при самостоятельном изучении курса. Во всех случаях рассмотренные примеры решения соответствуют многовариантным заданиям по теоретической механике [1], [2] и рабочей программе курса [3].

В ы б о р в а р и а н т о в з а д а ч. Каждому студенту-заочнику в начале изучения дисциплины выдается трехзначный шифр, который не зависит от номера зачетки, года рождения, фамилии и т.п. По таблице, приведенной в конце пособия [2], он выбирает двухзначные варианты для каждой отдельной задачи контрольной работы. Буквенные индексы из названий задач в таблице не использются, а только №№ по порядку, как они включены в контрольную работу. Например, по шифру 234 для контрольной работы № 1 значится:
«17 40 73 07». Следовательно, это будет соответствовать задачам:

№ 17 № 40 № 73 № 07

обычное заочное обучение С2 С4 К3 К4.

сокращенное заочное обучение С2 К3 Д1 Д5.

Хотя в пособии [2], например, имеются и другие задачи (С3, К2, Д7, Д8 и др.), но в контрольную работу № 1 они не включены. Какие задачи включаются в конкретную контрольную работу объявляется преподавателем во время сессии.

В ы б о р д а н н ы х п о в а р и а н т у. В каждой задаче имеется 10 схем и две таблицы с 10-ю наборами исходных данных. По 1-й цифре двузначного варианта выбирается № схемы, а по 2-й цифре – данные из первой (основной) таблицы. Например, по варианту 25 цифра 2 будет соответствовать № схемы, а цифра 5 – номеру строки или столбца в основной таблице, в которой заданы величины.

Для трехзначного варианта используются не только данные по тексту условия и основной таблице, но и параметры, приведенные в дополнительной таблице, имеющейся в каждой задаче. В этом случае данные дополнительной таблицы заменяют соответствующие данные, приведенные в тексте условия. Например, по варианту 357 следует выбирать: схему под № 3, данные из основной таблицы под № 5, а данные из дополнительной таблицы под № 7.

Конкретную методику использования трехзначных вариантов и выдачи вариантов для студентов дневного обучения определяет преподаватель, ведущий занятия.

 

 

 

 

СТАТИКА

 

Задача С1

Равновесие тела под действием плоской системы сил

 

Возьмем двузначный вариант 97, согласно которому схема должна быть по рис. С1.9(см. рис. С1 а), а данные – по тексту условия задачи и строке 7 таблицы С1.1 [1].

Из текста условия задачи следует, что на конструкцию действуют силы F₁ = 8кН,
F₂ = 12кН, направление которых определяется углами j₁=j₂= 30⁰, и пара сил с моментом М = 10кНм. Кроме этого, указано, что угол
g = 30⁰ а размер а нужно принять равным 0,4м.

В таблице С1.1 задано, что α=β=270⁰, а силы F₁ и F₂ приложены в точках Е и Д.

Тогда конкретная конструкция по варианту 97 с учетом приведенных данных будет выглядеть, как представлено на рис. С1 б, при этом построение начато с точки А.

Требуется определить реакции и моменты связей в точках В и А, а также произвести проверку полученных результатов.

Таким образом, задано: F₁ = 8, F₂ = 12кН; М = 10кНм; j₁= j₂= 30⁰, g=30⁰, α=β=270⁰, а =0,4м;

определить: R_A, R_B, M_B.

Решение

Освободим конструкцию от связей, заменим их действие реакциями и выберем систему отсчета в виде декартовых координат. Тогда расчетная схема будет выглядеть, как представлено на рис. С1 в.

Составим уравнения равновесия тела, включая в них заданные силы а также реакции и моменты связей.

=R_Acos60⁰+F₁cos30⁰+F₂cos60⁰=0; (1)

=R_Asin60⁰+F₁sin30⁰+F₂sin60⁰+R_B=0; (2)

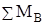= –R_Asin60⁰7 a –R_Acos60⁰2 a +M–F₁sin30⁰3 a –F₁cos30⁰2 a –F₂sin60⁰3 a +M_B=0. (3)

Решение уравнений начнем с простейшего:

(1)→ R_A= – (F₁cos30⁰+F₂cos60⁰)/cos60⁰= –(8cos30⁰+12cos60⁰)/cos60⁰= – 25,856кН.

Полученный результат показывает, что опорная плоскость должна обеспечить реакцию в точке А противоположного направления, в противном случае равновесие тела невозможно. Этого можно достигнуть поворотом опорной плоскости на 180⁰ и некоторым изменением конструкции для обеспечения контакта как, например, показано на рис. С1 г. Будем считать, что эти операции проведены и полученное направление реакции обеспечивается.

Тогда из других уравнений получим:

(2)→ R_B= –(R_Asin60⁰+F₁sin30⁰+F₂sin60⁰)=
= –((– 25,856)sin60⁰+8sin30⁰+12sin60⁰)=8,00кН;

(3)→ M_B=R_A(sin60⁰7+cos60⁰·2) a -M+F₁(sin30⁰·3+cos30⁰·2) a +F₂sin60⁰·3 a =
(–25,856)(sin60⁰·7+cos60⁰·2)0,4 –10 +8(sin30⁰·3+cos30⁰·2)0,4+12sin60⁰·3∙0,4=

= –60,227кНм.

Для проверки полученных результатов составим уравнение моментов сил относительно точки Е:

= –R_Asin60⁰4 a +M+F₂соs60⁰2 a +M_B+R_B3 a =
= –(–25,856)sin60⁰·4∙0,4+10+12соs60⁰·2∙0,4+(–60,227)+8,0∙3∙0,4=0,0001 ≈ 0.

Полученное отклонение от нулевого значения вполне можно объяснить погрешностями расчетов.

 

4 a

Задача С2

Равновесие плоской сочлененной конструкции

 

Берем двузначный вариант 36, согласно которому схема должна быть по рис. С2.3, а данные – по строке 6 таблицы С2.1 и тексту условия.

Из текста условия следует, что на конструкцию действуют: пара сил с моментом М=6кНм, распределенная нагрузка с интенсивностью, изменяющейся по линейному закону, для которой q_max = 3кН/м и две силы F₁=4кН и F₂=10кН. Кроме этого, указано, что размер а нужно принять равным 0,5м, а углы j₁ = j₂=60⁰. Угол γ в пособия [1] оказался пропущенным, поэтому примем его равным 30⁰.

По таблице С2.1 задано, что угол α=180⁰, β=270⁰, сила F₁ приложена в точке Д, сила F₂ – в точке Р, а распределенная нагрузка приложена на участке СД(АД). Заданная схема представлена на рис. С2 а.

Требуется определить реакции и моменты внешних связей, а также усилия в

промежуточном соединении, если конструкция находится в состоянии равно-весия.

С учетом приведенных выше данных скомпонуем конкретную схему и представим ее на рис. С2 б. В качестве связей, как видно по схеме, используются: стержень АС, неподвижный шарнир В, подвижный шарнир Р и скользящая плоская заделка Е.

Таким образом,

задано: М=6кНм, q_max = 3кН/м, F₁=4, F₂=10кН, а =0,5м, j₁=j₂=60⁰, γ=30⁰, α=180⁰, β=270⁰;

определить: X_B, Y_B, R_P, R_Е, М_Е, S_C.

 

Решение

Расчленим конструкцию в точках А и С, заменим действие связей реакциями и моментами, а вместо распределенной нагрузки представим ее равнодействующую Q. Тогда в качестве расчетных будем иметь две схемы, представленные на рисунках С2 в и С2 г. Системой координат «х,у» воспользуемся одной, которая показана на рис. С2 в. Таким образом, вместо одного сочлененного тела будем иметь два, для каждого из которых составим уравнения равновесия. При этом учтем, что

Q=0,5q_max·3 a =0,5·3·3·0,5=2,25кН.

Левая часть (рис. С2 в)

∑F_X=X_B+R_P+F₂cos30⁰+S_Csin30⁰=0; (1)

∑F_Y=Y_B+F₂sin30⁰+S_Ccos30⁰=0; (2)

∑M_B=R_P3 a +F₂cos30⁰3 a +S_Csin30⁰3 a +S_Ccos30⁰2 a =0. (3)

Правая часть (рис. С2 г)

∑F_X= –S_Аsin30⁰+F₁cos60⁰=0 (4)

∑F_Y=R_Е–S_Аcos30⁰+F₁sin60⁰–Q=0 (5)

∑M_А=F₁cos30⁰3 a +М+М_Е–Q2 а +R_Е7 а =0 (6)

Учитывая, что S_C=S_А, решение уравнений дает:

 

(4)→ S_А=F₁cos60⁰/sin30⁰=F₁=4кН;

(5)→ R_Е=S_Аcos30⁰–F₁sin60⁰+Q=4cos30⁰–4sin60⁰+2,25=2,25кН;

(6)→ М_Е= –F₁cos30⁰3 a -М+Q2 а –R_Е7 а = –4cos30⁰·3·0,5-6+2,25·2·0,5–2,25·7·0,5 =

= –16,821кНм;

(3)→ R_P= –(F₂cos30⁰·3+S_Csin30⁰·3+S_Ccos30⁰·2)/3=

= –(10cos30⁰·3+4sin30⁰·3+4cos30⁰·2)/3= –12,969кН;

(2)→ Y_B= –(F₂sin30⁰+S_Ccos30⁰)= –(10sin30⁰+4cos30⁰)= –8,464кН;

(1)→ X_B= –R_P–F₂cos30⁰–S_Csin30⁰= –(–12,969)–10cos30⁰–4sin30⁰=2,309кН.

Как видно по результатам расчетов, действительное направление реакций R_P, Y_B, а также момента скользящей заделки М_Е оказалось противоположным показанному на рисунках.

Проверка полученных результатов также может быть проведена аналогично той, которая выполнена при решении задачи С1. Но в этом случае одного уравнения моментов может оказаться недостаточно

 

 

Задача С3

Определение усилий в стержнях плоской фермы

 

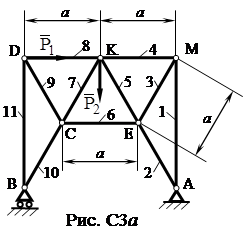Берем трехзначный вариант 674, согласно которому схема должна соответствовать рис. С3.6, основные данные взяты из текста и таблицы С3.1 по строчке 7, дополнительные данные – из колонки 4 таблицы С3.2.

Тогда из условия задачи следует, что заданные силы Р₁=20, Р₂=50кН, геометрический размер a составляет 1м.

В таблице С3.1 указано, что точками приложения сил являются Д и К, а требуется определить усилия в стержнях № 2 и № 7.

Из таблицы С3.2 следует, что уголы α₁=0, а α₂=270⁰.

Согласно этим данным исходная схема должна выглядеть как представлено на рис С3 а.

Используя метод «вырезания узлов», необходимо определить усилия в стержнях № 2 и № 7 и указать, какому воздействию они подвержены – сжатию или растяжению.

Таким образом, задано: Р₁=20(в точке Д), Р₂=50кН(в точке К), a = 1м, α₁=0, α₂=270⁰;

определить: S₂, S₇.

Решение

Стержень 2 входит в узел А, связанный с неподвижным шарниром, поэтому возникающее в нем усилие можно определить после нахождения реакций этого шарнира. А вот стежень 7 входит в узлы С и К, в которых сходятся по 4 стержня. Так как для одного «вырезанного узла» можно определить через уравнения равно-

весия только 2 неизвестных, то придется «вырезать» сначала узел В, затем Д и после этого узел С.

Прежде всего, составим расчетную схему для определения реакций связей в точках А и В и представим ее на рис С3 б. Тогда, рассматривая всю ферму как одно целое, получим уравнеия равновесия.

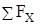=Х_А+Р₁=0; (1)

= –Р₁2 а cos30⁰+P₂ a –R_B2 a =0 (2)

= –Р₁2 а cos30⁰–P₂ a +Y_A2 a =0. (3)

Решение уравнений дает:

(1)→ Х_А= –Р₁= –20кН(направлено в противоположную сторону);

(2)→ R_B=(–Р₁2cos30⁰+P₂)/2=(–20∙2cos30⁰+50)/2=7,680кН;

(3)→ Y_A=(Р₁2cos30⁰+P₂)/2=(20∙2cos30⁰+50)/2=42,320кН.

Рассмотрим теперь равновесие узла А, представив расчетную схему на рис С3 в. При этом уже вычисленные проекции реакций Х_А и У_А покажем на схеме с учетом их действительного направления и предположим, что стержни 1 и 2 подвергнуты растяжению. Тогда

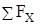= –S₂sin30⁰ –X_A=0; (4)

=S₁+Y_A=0. (5)

Решение уравнений дает:

(4)→ S₂= –X_A/sin30⁰= –20/sin30⁰= –40кН (стержень сжат).

Усилие S₁ по условию задачи определять не требуется.

Следующим «вырезаем» узел В. Для известных по величине сил показываем их действительное направление, а неизвенстные реакции S₁₀ и S₁₁ направим от узла, предполагая растяжение стержней. Расчетная схема узла представлена на рис. С3 г.

Уравнения равновесия узла будут иметь вид

=S₁₀sin30⁰=0; (6)

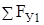=S₁₁+R_B=0. (7)

Из уравнения (6) следует, что S₁₀=0, а уравнения (7) дает:

S₁₁= –R_B= –7,680кН (стержень сжат).

Для рассмотрения равновесия узла Д также условимся заданные силы показывать по их действительному направлению, а стержни 8 и 9 предположим растянутыми. Тогда схема сил будет выглядеть, как представлено на рис. С3 д. Уравнения равновесия узла Д будут иметь вид:

=Р₁ +S₈+S₉sin30⁰=0; (8)

=S₁₁+-S₉соs30⁰=0. (9)

Требуемое усилие S₉ получим из уравнения (9):

S₉=S₁₁/соs30⁰=7,680/соs30⁰=8,868кН (стержень растянут).

Так как усилие S₈ определять не требуется, то уравнение (8) остается не использованным.

Расчетная схема, касающаяся равновесия узла С, представлена на рис. С3 е, при этом предполагается, что все стержни подвергнуты усилиям растяжения, хотя ранее уже получено, что S₁₀=0. Уравнения равновесия узла будут иметь вид:

= –S₉sin30⁰+S₇sin30⁰–S₁₀sin30⁰+S₆=0; (10)

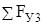=S₉соs30⁰+S₇соs30⁰–S₁₀соs30⁰=0. (11)

Решение уравнения (11) дает:

S₇=S₁₀ – S₉=0–8,868= –8,868кН (стержень сжат).

Если бы требовалось определить усилие в стержне 6, то можно было бы использовать и уравнение (10).

 

 

Задача С4

Равновесие тела под действием произвольной
пространственной системы сил

 

Возьмем трехзначный вариант 978, что соответствует схеме по рис. С4.9, основным данным по строчке 7 таблицы С4.1 и дополнительным данным по колонке 8 таблицы С4.2.

Из текста условия задачи следует, что вес большей плиты Р₁ составляет 5кН, вес меньшей – Р₂ =3кН, а на конструкцию действуют сила F=50кН, пара сил и усилия в ветвях ремня Т=1,0 и t=0,5кН, передающиеся на шкив. Кроме этого, заданы линейные размеры и углы: а =0,4м, радиус шкива R=0,1м, y=60⁰, q=30⁰.

В таблице С4.1 указано, что сила F должна быть приложена в точке N, угол j, определящий ее направление, должен отсчитываться от оси «х» в сторону оси «у», а момент пары сил М₁ = –30кНм.

Из дополнительной таблицы С4.2 следует, что угол j нужно принять равным –150⁰, в отличие от того, что задано по тексту.

Требуется определить реакции связей в точках А и В конструкции и усилия, возникающие в стержнях.

Таким образом, задано:

Р₁=5, Р₂ =3, F=50, Т=1,0, t=0,5кН;
М₁= – 30кНм; y =60⁰, q =30⁰, j= –150⁰; а =0,4, R=0,1м;

определить: Х_А, У_А, Z_A, Х_В,У_В, S_L.

 

Решение

С учетом приведенных данных представим схему по варианту на рис. С4 а и превратим ее в расчетную. Для этой

цели в центрах тяжести С₁ и С₂ приложим силы тяжести обеих плит 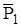и , в точке N –заданную силу с учетом угла j =-150⁰, а действие связей заменим

соответствующими реакциями. При этом предполагается, что стержень в точке L подвержен растяжению, а момент пары сил М₁ показан без учета его знака.

Составим уравнения равновесия всей конструкции согласно схеме, представленной на рис. С4 а.

=0 (1)

=0; (2)

=0; (3)

–S_Lsinψ4 a –P₁2 a –P₂2 a –Fsin30⁰2 a –Tsinθ5 a =0; (4)

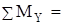S_Lsinψ3 a +S_Lcosψ2 a +Fcos30⁰2 a +P₁1,5 a +P₂3 a +TR–tR=0; (5)

–X_B4 a +S_Lcosψ4 a –Fsin30⁰3 a +M₁+t5 a +Tcosθ5 a =0. (6)

Решение уравнений дает:

(2)→ Y_A=Fsin30⁰=50sin30⁰=25кН;

(5)→ S_L= –[(Fcos30⁰·2+P₁·1,5+P₂·3) a +(T–t)R]/(sinψ3+cosψ2) a =

–[(50cos30⁰·2+5·1,5+3·3)0,4+(1–0,5)0,1]/(sin60⁰·3+cos60⁰·2)0,4= –28,690кН;

(6)→ X_B=[(S_Lcosψ·4–Fsin30⁰·3+t·5+Tcosθ·5) a +M₁]/4 a =

=[((–28,69)cos60⁰·4–50sin30⁰·3+0,5·5+1·cos30⁰·5)0,4+(–30)]/(4·0,4)= –50,137кН;

(4)→ Z_B=(S_Lsinψ·4+P₁·2+P₂·2+Fsin30⁰·2+Tsinθ·5)/5=

((–28,69)sin60⁰·4+5·2+3·2+50sin30⁰·2+1·sin30⁰·5)/5= – 6,177кН;

(3)→ Z_A= –Z_B+S_Lsinψ+P₁+P₂+Tsinθ=

= –(–6,177)+(–28,69)sin60⁰+5+3+1·sin30⁰= – 10,169кН;

(3)→ X_A=-X_B+S_Lcosψ+Fcos30⁰+Tcosθ+t=

= –(–50,137)+(–28,69)cos60⁰+50cos30⁰+1·cos30⁰+0,5 = 80,459кН.

Полученные результаты показывают, что действительные реакции X_B, Z_A и Z_B оказались противоположными показанному на схеме, а стержень О₁L вместо растягивающей испытывает сжимающую нагрузку.

 

 

КИНЕМАТИКА

 

 

Задача К1

Кинематика точки

 

Возьмем вариант 77, согласно которому должны использоваться данные рис. К1.7 и таблицы К1.1 –7-й столбец [1], в которых заданы уравнения движения точки в декартовых координатах в виде х=4соs²(pt/6); у = 5sin(pt/6),см.

По тексту условия задачи указано, что в момент t=2с движущаяся точка М достигает точки Д и далее движется по окружности радиуса R=5см с ускорением а _t= 2t₁–1 см/с² в течение t₁ = 3с до точки Е.

Требуется определить: для 1-го участка – уравнение траектории, скорость, ускорение и радиус кривизны траектории в точке Д; для 2-го участка – положение точки Е, ее скорость, касательное и нормальное ускорения. Кроме этого, необходимо построить графически оба участка траектории и показать все полученные величины.

Таким образом, задано: х=4соs²(pt/6), у = 5sin(pt/6)см, t=2с; R=5см,
а _t= 2t₁–1,см/с², t₁ = 3с;

определить: у=f(x), ρ_Д, V_Д, а _Д; φ_Е, V_Е, , .

Решение

Возведем второе уравнение движения в квадрат и получим

х/4=соs²(pt/6);

(у/5)²=sin²(pt/6).

После сложения уравнений имеем уравнение траектории в виде

,

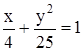которое показывает, что это парабола

. (1)

В момент времени t=2с точка занимает положение, определяемое координатами:

х=4соs²(pt/6)=4соs²(2p/6)=4соs²60⁰=4·0,25=1см;

у=5sin(pt/6)=5sin(2p/6)=5·0,866=4,33см.

При t=0 координаты точки составляли:

х=4соs²0=4см; у=5sin0см=0.

Проекции скорости точки:

при t=2c→ V_x= –(4p/3)sin(2p/3)= –(4p/3)sin120⁰= –3,6275см/с.

при t=2c→ V_у=(5p/6)соs(2p/6)=(5p/6)соs60⁰=1,309см/с.

Следовательно,

V_Д= 3,856см/с.

Проекции ускорения точки:

;

при t=2c→ а _х= –(4π²/9)соs(2π/3)= –(4π²/9)соs(120⁰)=2,193cм/c².

при t=2c→ а _у= –(5π²/36)sin(2π/3)= –(5π²/36)sin120⁰= –1,187cм/c².

Тогда

а _Д= =2,493см/с².

Далее

а _τ=(V_x а _x+V_y а _y)/V=[(–3,6275)(2,193) + (1,309)(–1,187)]/3,856= –2,466см/с².

а _n= =0,366см/с².

Следовательно,

ρ=V_Д²/ а _n=3,856²/0,366=40,625см.

Представим полученные данные на рис К1 а.

Дальнейшее движение по окружности:

= .

При t₁=0→ V_Д=C₁=3,865см/с, поэтому

.

В момент времени t₁=3c скорость в точке Е будет

V_E=3² –3 +3,865=9,865см/с.

Следовательно, для точки Е

а _n=V²/R=9,865²/5=19,464cм/с²;

а _t= 2t₁–1=2·3-1=5см/с².

Положение точки Е

s= .

Так как для точки Д→ s=0, следовательно, С₂=0, а

s_Е=3³/3-3²/2+3,865·3=16,095см,

что соответствует углу

φ=s/R=16,095/5=3,219рад=3,219·180/π=184,4⁰

как и представлено на рис К1 а.

 

Задача К2

 

Возьмем трехзначный вариант 729, согласно которому схема должна быть по рис. К2.7, основные данные – из табл. К2.1 (столбец 2), дополнительные данные – из табл. К2.2 (столбец 9).

Из текста условия следует, что радиусы ступеней колес составляют: r₁=4, R₁=10, r₂=5, R₂=12, r₃=8, R₃=16см, а расчетный момент времени t = 2с.

В табл. К2.1 задан закон изменения 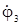= 3t²-2t с^-1, при этом положительное направление отсчета – против хода часовой стрелки.

По таблице К2.2 для заданного момента времени требуется определить: скорость груза 4 V₄, угловую скорость блока 1 w₁, угловое ускорение блока 3 e₃, ускорение точки С блока 1 а _С, количество оборотов блока 2 z₂ за заданное время.

Таким образом, задано: 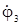= 3t²-2t, с^-1; r₁=4, R₁=10, r₂=5, R₂=12, r₃=8, R₃=16см; t = 2с;

определить: V₄, w₁, e₃, а _С, z₂.

 

Решение

Прежде всего, определим угловое ускорение блока 3.

с^-2.

Следовательно, при t =2с

e₃=6·2–2=10с^-2.

Используем заданную схему, приведенную на рис. К2 а, в качестве расчетной.

В момент времени t = 2с угло-вая скорость

w₃=3t²-2t=3·2²-2·2=8с^-1.

С учетом этого

V₄=w₃r₃=8·8=64см/с.

Используя передаточные отношения, получим

,

следовательно,

( 3t²-2t)16/5=3,2(3t²–2t)с^-1.

При t =2с

w₂=3,2(3t²–2t)=3,2(3·2²–2·2) =25,6с^-1;

при t =0→ w₂=0.

Однако угловая скорость w₂ становится равной нулю еще в один момент времени, а именно

3,2(3t²-2t)=0 → t=2/3=0,667с.

Это означает, что механизм движется сначала в одну сторону, а затем – в другую. Поэтому определим углы поворота.

=3,2(t³–t²) +С₁.

Так как отсчет угла предусмотрен от нулевого положения, то С₁=0 и угол φ₂ соответственно равен

t=0,667с→ φ₂₁=3,2(t³–t²)=3,2(0,667³–0,667²)= –0,474рад;

t=2с→ φ₂₂=3,2(2³-2²)=12,8рад.

Тогда общее количество оборотов шестерни 2 в ту и другую стороны составит

z₂=2(|φ₂₁|/2π) +(φ₂₂/2π) = 2(0,447/2π)+(12,8/2π)=2(0,071)+2,037= 2,179об.

Так как заданная точка С принадлежит блоку 1, необходимо определить его угловую скорость и угловое ускорение. Используя передаточные отношения, получим:

w₁=w₂(R₂/r₁)=w₃(R₂R₃/r₁r₂)=8(12·16/4·5)=76,8с^-1;

e₁=e₂(R₂/r₁)=e₃(R₂R₃/r₁r₂)=10(12·16/4·5)=96с^-2.

Тогда

а _Сⁿ=w₁²R₁=76,8²·10=58982,4см/с²=589,8м/с²;

а _С^τ=e₁R₁=96·10=960см/с²=9,6м/с²;

а _С= =589,9м/с².

Все полученные величины представлены на рис. К2 а.

 

 

Задача К3

Плоскопараллельное движение твердого тела

 

Возьмем двузначный вариант 49, для которого схема должна быть по рис. К3.4, а данные – по таблице К3.1 столбец 9.

По тексту условия заданы: угловая скорость и угловое ускорение звена 1
w₁ = 4с^-1, e₁ = 10 с^-2; размеры звеньев механизма l ₁ = 0,4м, l ₂ = 4 l ₁, l ₄ = 5 l ₁, l ₅ =2 l ₁,
r₃ = 0,2м, R₃ = 1,5r₃, R = 3R₃; углы g = 60⁰, j₃ = 120⁰.

Из таблицы К3.1 следует: j₁=0, j₂=60⁰, b=150⁰.

Исходная схема с учетом этих данных представлена на рис. К3 а, при этом АД=ДВ.

Требуется определить скорости точек А, К, Е; угловые скорости звеньев w₂, w₃, w₄; ускорение точки В и угловое ускорение e₂, т.е. звена 2.

Таким образом, задано: w₁ = 4с^-1, e₁ = 10 с^-2,
l ₁ = 0,4, l ₂ = 1,6, l ₄ = 2,0, l ₅= 0,8м, r₃ = 0,2, R₃ = 0,3,
R = 0,9м; j₁=0, j₂=60⁰, j₃ = 120⁰, b=150⁰, g = 60⁰; АД= ДВ=0,8м;

определить и построить: , w₂, w₃, w₄, 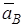, e₂.

Решение

Воспользуемся схемой, представленной на рис К3 а и построим векторы скоростей точек А, В, Д, Е, К, мгновенные центры скоростей Р₂ и Р₃ и покажем угловые скорости w₂, и w₃. Мгновенный центр скоростей звена 4 уходит в бесконечность, поэтому w₄= 0. Кроме этого, АД=ДВ=АР₂, поэтому треугольник АДР₂ равностопронний.

Скорость точки А:

V_A=w₁О₁А=w₁ l ₁=4·0,4=1,6м/с.

Так как АP₂=ДP₂, то

V_Д=V_A=1,6м/с.

По теореме о проекциях скоростей (на прямую АВ) получим

V_Вcos60⁰=V_Acos30⁰→ V_В=V_Atg60⁰=1,6tg60⁰=2,771м/с.

Скорости V_Д и V_Е оказались параллельными, поэтому

V_Е = V_Д=1,6м/с.

Угловыю скорости w₂ и w₃ найдем по формулам:

w₂ =V_A/АР₂ = V_A/0,5 l ₂= 1,6/(0,5·1,6)= 2с^-1;

w₃ =V_В/ВР₃ =V_В/R₃ = 2,771/0,3=9,237с^-1.

Тогда

V_К=w₃·КР₃= =3,33м/с.

Для определения ускорений воспользуемся схемой, представленной на рис. К3 б.

Прежде всего, представим ускорение точки В в виде векторной формулы, учитывая, что точка В движется по окружности радиуса R+R₃, т.е.

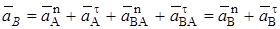. (1)

Определим составляющие, входящие в это выражение.

а _Аⁿ=ω₁²О₁А=ω₁²l₁=4²·0,4=6,4м/с².

а _А^τ=ε₁О₁А=ε₁l₁=4·0,4=1,6м/с².

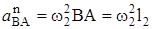=2²·1,6=6,4м/с².

=6,39м/с².

Остальные составляющие пока остаются неизвестными, поэтому построим многоугольник ускорений точки В согласно выражения (1). Если выдержать масштаб для векторов ускорений, то получим графическое решение задачи. Штриховые линии на рис. К3 б показывают, как следовало направлять заранее неизвестные ускорения при построении многоугольника.

Проведем из точки В оси координат «х,у», чтобы одна из осей была направлена вдоль АВ и спро-ектируем на них выра-жение (1).

а _Вх= – а _Аⁿcos30⁰+ а _А^τsin30⁰+ а _BA^τ= а _Bⁿsin30⁰+ а _B^τcos30⁰. (2)

а _Ву= а _Аⁿcos60⁰+ а _А^τsin60⁰– а _BAⁿ= а _Bⁿsin60⁰– а _B^τcos60⁰. (3)

Из выражения (3) получим

=

=0,5(–6,4cos30⁰–1,6sin30⁰+6,4+6,39sin60⁰)=2,796м/с².

Следовательно,

=6,975м/с².

Из выражения (2) найдем, что

а _BA^τ= а _Аⁿcos30⁰– а _А^τsin30⁰+ а _Bⁿsin30⁰+ а _B^τcos30⁰=

=6,4cos30⁰–1,6sin30⁰+6,39sin30⁰+2,796cos30⁰=10,358м/с².

В свою очередь, это позволяет определить, что

.

Направление всех полученных величин показано на рис. К3 б. Если бы какая-либо из них получилась со знаком «минус», то это означало бы, что не выдержан масштаб построения или при решении допущена ошибка.

 

 

Задача К4

Сложное движение точки

 

Возьмем трехзначный вариант 935. Это означает, что схема должна быть по рис К4.9, данные из таблицы К4.1 по строке 3, а дополнительные данные, касающиеся направления движения, – по строке 5 таблицы К4.2.

Из таблицы К4.1 имеем закон изменения угла поворота тела

j = p(4t+t²)/3 рад

и закон относительного движения точки по окружности

S = 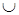АМ =(2p/3)Rcos(p(1+t/6))см.

Кроме этого, из таблицы К4.2 следует, что угол поворота j должен отсчитываться против хода часовой стрелки, координата S – по ходу, а расчетное время t должно составлять 1с (в отличие от двузначных вариантов, для которых эти параметры заданы по тексту условия и на схемах).

Из условия задачи следует, что радиус кольца трубки R составляет 30см, а требуется определить абсолютную скорость и абсолютное ускорение точки в заданный момент времени.

Таким образом, задано: S = 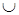АМ=(2p/3)Rcos(p(1+t/6))см, j = p(4t+t²)/3 рад, R=30см, t=1c;

определить: V, а.

 

Решение

С учетом заданных условий схема по варианту должна выглядеть, как пред–

ставлено на рис. К4 а.

Прежде всего, определим положение точки в заданный момент времени, т.е.

S = АМ =(2p/3)Rcos(p(1+t/6))=(2p/3)Rcos((7/6)p)=

=(2p/3)Rcos210⁰= см.

Это соответствует углу

рад= –103,9 .

Движение точки по вращающемуся кольцу следует считать относительным, а движение вместе с кольцом – переносным. Используем в качестве расчетной схему, представленную на рис. К4 б.

Относительное движение

Для момента времени t=1c относительная скорость составит

=16,45см/с.

.

При t=1c относительное касательное ус-корение

14,92см/с².

Для определения относительного нор-мального ускорения используем формулу

9,02см/с².

Переносное движение

Прежде всего определим радиус переносного вращения с учетом положения точки и величины угла α:

R_e=R–Rsin(α–90⁰)=30(1–sin14⁰)=17,24см.

Для определения угловой скорости и углового ускорения продифференцируем угол φ.

=6,28с^-1.