а) х1
б) х1х3
в) х1vх2
г) х1х2х3
д) х1(х2vх3)
218.
Выражения `х1, х1х3, х1х2х3 называются … конъюнкции
219.
Конституэнтой единицы называется элементарная …, содержащая все аргументы данной функции
220.
Конституэнта единицы содержит все аргументы данной функции и сама функция на данном наборе аргументов принимает значение …
221.
Элементарная конъюнкция, содержащая все аргументы данной функции, причем сама функция на данном наборе аргументов принимает значение 1, называется …
222.
Конституэнтой единицы называется элементарная конъюнкция, содержащая …, причем сама функция на данном наборе аргументов принимает значение 1
А) все аргументы данной функции
Б) отдельные аргументы данной функции
В) аргументы равные единице
223.
Логические выражения соответствующие СДНФ заданной функции
а)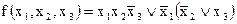 
б) 
в) 
224.
Функция алгебры логики
записана в стандартной форме … (аббревиатура)
225.
Совершенной ДНФ называется конъюнкция … …
226.
Конъюнкция конституэнт единицы называется … (аббревиатура)
227.
Выражение представлено в форме
А) ДНФ
Б) КНФ
В) СДНФ
Г) СКНФ
228.
Выражение представлено в форме
А) ДНФ
Б) КНФ
В) СДНФ
Г) СКНФ
229.
Способы получениясовершенной дизъюнктивной нормальной формы логической функции
А) по таблице истинности
Б) методом ввода недостающих аргументов
В) по теореме разложения
Г) методом импликантных таблиц
230.
Основу метода ввода недостающих аргументов составляют
А) закон поглощения
б) тождество 
В) теорема разложения
г) тождество 
231.
Стандартная форма, в которой представлена каждая логическая функция (аббревиатура)
а) 
б) 
в) 
г)
232.
Цель минимизации логической функции заключается
А) в равносильном преобразовании функции и упрощении функциональной схемы
Б) в исключении из логического выражения условных обозначений функций
В) в сокращении числа аргументов функции до минимума и, как следствие, упрощении схемной реализации
233.
Для минимизации логических функций применяются методы
А) матричные
Б) аналитические
В) комбинированные
Г) табличные
234.
Основу всех методов минимизации логических функций составляют законы … и …
235.
Все наборы аргументов логических функций делятся на
а) запрещенные
Б) стандартные
в) условные
г) рабочие
236.
Соседние пары двоичных чисел
| а) | 0 0 0 1 |
| 1 1 1 1 |
| б) | 0 0 1 0 |
| 0 0 1 1 |
| в) | 0 1 1 1 |
| 1 1 1 0 |
237.
Соседними числами называются двоичные числа, отличающиеся:
а) Одним разрядом
б) Не более чем двумя разрядами
в) Значением функции
238.
Метод Квайна-Мак-Класски основан на законах алгебры логики
а) Поглощения
б) Двойного отрицания
в) Склеивания
г) Повторения
д) Инверсии
239.
Метод Квайна-Мак-Класски позволяет получить
А) тупиковые ДНФ
Б) минимальные ДНФ
В) сокращенные ДНФ
240.
Метод Квайна-Мак-Класски позволяет получить …ДНФ
241.
Результат минимизации функции 
методом Квайна
а)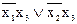 
б) 
в) 
г) 
д) 
242.
Результат минимизации функции 
методом Квайна
а)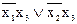
б)
в)
г)
д)
244.
Результат минимизации функции 
методом Квайна
а)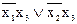
б)
в)
г)
д)
245.
Результат минимизации функции 
методом Квайна
а)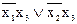
б)
в)
г)
д)
246.
Результат минимизации функции 
методом Квайна
а)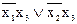
б)
в)
г)
д)
247.
Метод импликантных таблиц позволяет получить
А) тупиковые ДНФ
Б) минимальные ДНФ
В) сокращенные ДНФ
248.
Метод импликантных таблиц позволяет получить … ДНФ
249.