Лекция Произведения векторов
Скалярное произведение векторов
Скалярным произведением двух векторов называется число, равное произведению абсолютных величин этих векторов на косинус угла между ними 
, где 
.
Для обозначения скалярного произведения двух векторов возможно использование выражения 
.
Из физики известно, что если 
- постоянная сила, действующая на материальную точку, а 
- вектор перемещения точки под действием этой силы, то работа, совершаемая силой на участке l, равна 
.
Свойства скалярного произведения
скалярное произведение векторов коммутативно;
числовой множитель можно выносить за знак скалярного произведения;
скалярное произведение дистрибутивно относительно сложения векторов;
скалярное произведение равно нулю, если вектора ортогональны или один из векторов равен нулю;
скалярное произведение вектора самого на себя равно квадрату его длины, при этом 
, поэтому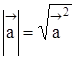 
;
.
Выражение скалярного произведения через проекции перемножаемых векторов
Для двух векторов с известными координатами:
и 
имеет место следующее равенство:
.
Принимаем во внимание, что: 
, поскольку это есть скалярные квадраты, например 
,
, т.к. это есть скалярные произведения перпендикулярных векторов.
Замечание: скалярное произведение двух векторов равно сумме парных произведений одноименных координат векторов.
Условие перпендикулярности векторов: для того, чтобы два вектора были перпендикулярны, необходимо и достаточно, чтобы их скалярное произведение было равно нулю, т.е. сумма парных произведений их одноименных проекций равнялась нулю.
Косинус угла между векторами
|
|
По определению скалярного произведения 
, откуда можем выразить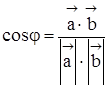 
, если известны координаты векторов, получаем:
.
Пример 1. Вычислить абсолютную величину вектора 
, если известно, что 
, 
, 
, 
.
Согласно свойству скалярного произведения 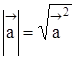, поэтому 
;
учитывая, что 
, 
, 
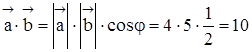, получаем 
.
Пример 2. Найти координаты вектора 
, если известно, что 
, 
, а также 
.
Нам известно, что 
, примем, что эти векторы коллинеарны, т.е. 
, таким образом 
, где 
, откуда 
. Однако нам неизвестен знак скалярного сомножителя. Для его определения рассмотрим угол 
, который является тупым, т.е. проекция вектора на ось Oz (орт 
) должна быть отрицательной. Что касается проекции вектора 
на ось Oz (орт ), она положительна (равна 1), таким образом, вектора и имеют проекции разных знаков на ось Oz, т. е. вектора разнонаправлены 
. Приходим к выводу, что 
имеет отрицательный знак 
и координаты вектора находятся таким образом:
;
;
.
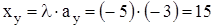Вектор 
.
Пример 3. Найти угол , если известно, что 
, 
и
Раскроем скобки и приведем подобные
.
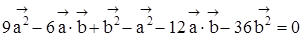
Векторное произведение
Упорядоченная тройка некомпланарных векторов называется правой, если из конца третьего вектора кратчайший поворот от первого ко второму виден против часовой стрелки. В противном случае тройка называется левой.
Начала векторов тройки предполагаются совмещенными.
В данном случае тройка , 
, - правая тройка (кратчайший поворот от к с конца вектора виден происходящим против часовой стрелки), а тройка , , - левая тройка (кратчайший поворот от к с конца вектора виден происходящим по часовой стрелке).
|
|
Векторным произведением двух векторов называется вектор, который обозначается 
или 
и определяется следующим образом:
, где - длина этого вектора равна произведению длин перемножаемых векторов на синус угла между ними;
, 
– этот вектор перпендикулярен каждому из перемножаемых векторов;
векторы , , образуют правую тройку векторов.
Из первого условия следует, что модуль вектора численно равен площади параллелограмма, построенного на векторах и как на сторонах 
.
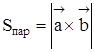Свойства векторного произведения
;
;
;
, или 
, или 
;
, поскольку 
.