ТЕМА 5 (продолжение). ЗАКОНЫРАСПРЕДЕЛЕНИЯ
п. 7. Биномиальное распределение
Если вероятности, соответствующие возможным значениям ДСВ определены по формуле Бернулли, то закон распределения носит название биномиального. Биномиальное распределение вероятностей возможно в случае, когда производится n независимых испытаний, в каждом из которых событие А может появиться с вероятностью p, либо не появиться с вероятностью q = 1 – p.
В табличной форме этот закон имеет следующий вид:
| Х = k | … | п | |||
| 
| 
| 
| … | 
|
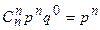
Вероятности 
представляют собой члены бинома Ньютона, благодаря чему распределение и получило своё название. В соответствие с формулой бинома:
+ 
+ 
+…+ 
= 
.
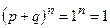Таким образом, все возможные значение случайной величины, распределённой по биноминальному закону, образуют полную группу событий.
Пример. Вероятность рождения мальчика равна 0,5. Составить закон распределения случайной величины Х – числа родившихся мальчиков в семье имеющих трех детей.
Решение. Величина X может принять одно из возможных значений: x 1 = 0; x 2 = 1; x 3 = 2; x 4 = 3. Вероятности того, что величина X примет эти значения, соответственно равны:
; 
;
; 
.
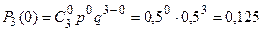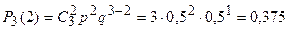Искомый биномиальный закон распределения имеет вид:
| Х = k | ||||
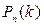
| 0,125 | 0,375 | 0,375 | 0,125 |
Контроль: 0,125 + 0,375 + 0,375 + 0,125 = 1.
п. 8. Распределение Пуассона
Дискретная случайная величина Х имеет закон распределения Пуассона, если вероятности ее возможных значений вычисляются по формуле Пуассона.
Pn (k) ≈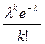 
, где 
.
Этот закон называют также законом распределения вероятностей массовых (n велико) и редких (p мало) событий.
В табличной форме этот закон распределения имеет вид
| Х = k | … | п | |||
| 
| 
| 
| … | 
|
Убедимся, что все возможные значение случайной величины, распределённой по закону распределения Пуассона, образуют полную группу событий и, следовательно, сумма их вероятностей равна 1.
п. 9. Геометрическое распределение
Предположим, что эксперимент или опыт осуществляют до первого появления события А. Число проведенных попыток будет целочисленной случайной величиной 1,2,.... Вероятность появления события А в каждом опыте не зависит от предыдущих и составляет p, а непоявления 
. Как только событие А появилось – испытание заканчивается.
Пусть в первых 
-ых испытаниях событие А не наступило, а в 
- ом испытании появилось. Вероятность этого сложного события по теореме умножения вероятностей независимых событий равна
,
где k = 1, 2, 3.
Данное распределение называют геометрическим, так как его последовательно полученные значения представляют собой бесконечную убывающую геометрическую прогрессию с первым членом p и знаменателем q (
):
p, qp, q 2 p, …qk - 1 p, …
В табличной форме геометрический закон распределения имеет вид
| Х = k | … | п | |||
| 
| 
| 
| … | 
|
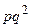
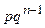
При проверке условия образования значениями ДСВ полной группы событий используем формула суммы бесконечной геометрической прогрессии:
.
п. 10. Гипергеометрическое распределение
Рассмотрим задачу. Пусть имеется некоторое множество однотипных элементов, число которых равно N, из них п элементов обладают признаком А, а остальные 
элементов признаком В. Из этого множества наугад берут т элементов. Обозначим через Х дискретную случайную величину «k элементов, обладающих признаком А, среди m случайно отобранных элементов». Очевидно, что случайная величина Х может принимать следующие возможные значения: 0, 1, 2, …, 
.
Найдем число исходов, благоприятствующих появлению события Х = k (среди взятых m элементов ровно k обладают признаком А). При этом наугад изъятые из общего количества m элементов одновременно удовлетворяю двум условиям:
1) среди них есть k элементов с признаком А (выбранные из общего числа п элементов с этим признаком);
2) среди них есть 
элементов с признаком В (выбранные из общего числа N – п элементов с этим признаком)/
Тогда число исходов, благоприятствующих появлению события Х = k будет равно произведению сочетаний 
.
Искомая вероятность по классическому определению вероятности случайного события равна отношению числа исходов, благоприятствующих событию Х = k, к общему числу элементарных исходов
.
Данная формула определяет закон распределения вероятностей, которое называют гипергеометрическим.
В табличной форме записи этот закон распределения имеет вид
| Х = k | … |
| |||
|
| 
| 
| 
| … | 
|
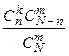
п. 10. Равномерный закон распределения
Целочисленных случайная величина Х имеет равномерный закон распределения, если вероятности ее возможных значений одинакова от эксперимента к эксперименту и вычисляются формуле
.
В табличной форме записи равномерный закон распределения имеет вид:
| Х = k | … | п | |||
| 
|
|
| … |
|
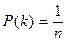
Очевидно, что все значения случайной величины, распределённой по равномерному закону, образуют полную группу событий:
.