Шесть факторов сложных процентов

Факторы сложных процентов

Процентная ставка – это отношение суммы процентных денег, выплачиваемых за фиксированный отрезок времени, к величине ссуды.

Например: 10 руб. – процентный деньги = 0,1 (10%) – процентная ставка.

100 руб. – ссуда

Всего выплачивается 110 руб.

Период начисления – это срок, к которому приурочена процентная ставка.

Существуют:

Простые процентные ставки – это когда ставка процентов применяется к одной и той же начальной сумме.

Пример:

Мы кладем 100 руб. под 10% годовых по простой процентной ставке:

- в первый год мы получим 110 руб, т.е. 10 руб. в год;

- во второй год – 120 руб. = 110 +10 руб. в год;

и т.д.

Сложные процентные ставки (сложные проценты) – это когда ставка процентов применяется к сумме с начисленными в предыдущих периодах процентами.

Пример:

Мы кладем 100 руб. по 10% годовых под сложные проценты:

- в первый год мы получим:

FV = 100 + 100 * 0,1 = 100*(1+0,1) = 110 руб.,

- во второй год мы получим:

FV = 100*(1+0,1)*(1+0,1) = 100 * (1+0,1)² = 100 * 1,21 = 121 руб.,

и т.д.

Эта модель начисления процентов и есть модель сложных процентов.

Существуют 6 функций (факторов) сложных процентов.

В первых трёх функциях использована концепция наращивания.

Наращивание (накопление) – это принцип, используемый для расчёта процентных доходов или расходов по уплате процентов.

(1+Е)^t – множитель наращивания.

В остальных трёх функциях используется концепция дисконтирования, обратная концепции наращивания.

Дисконтирование – это сокращение величины будущего дохода до уровня их текущей стоимости по обусловленной ставке дисконта (приведение будущей стоимости к современной величине).

PV = FV*

= α _t – коэффициент дисконтирования.

Значения коэффициента дисконтирования и множителя наращивания для целых чисел t м. взять в таблицах учебников (напр. в задачнике Грабового П.Г. «Экономика и управление недвижимостью»).

Шесть факторов сложных процентов

Существуют 6 функций (факторов) сложных процентов.

В первых трёх функциях использована концепция наращивания.

Наращивание (накопление) – это принцип, используемый для расчёта процентных доходов уплаты процентов.

В остальных трёх функциях используется концепция дисконтирования, обратная концепции наращивания.

Дисконтирование – это сокращение величины будущего дохода до уровня их текущей стоимости по обусловленной ставке дисконта.

1. Фактор накопления суммы денежной единицы – это будущая стоимость вложения, равного единице ( колонка 1).

Используется для определения будущей стоимости денег (FV) при известной их текущей стоимости (PV)

(1+Е)^t – это и есть 1 фактор.

Графически:

 

PV FV-?

t = 0 t

Пример:

Мы рассматривали в сложных процентных ставках.

Положили 1000руб под 10% годовых на 5 лет.

FV= 1000*(1+E)⁵ = 1000 * 1,61051 = 1610,51 руб.

2. Фактор накопления денежной единицы за период (2 колонка).

Это будущая стоимость единичного вложения за период или будущая стоимость аннуитета.

Аннуитет – это поток положительных платежей с одинаковыми временными интервалами между собой.

С помощью метода аннуитета рассчитывается рентабельность инвестиций, определяется арендная плата, рассчитываются годовые затраты и определяется размер амортизационного фонда.

Графически это можно представить:

Известна сумма единичных платежей (R)

 

^{0 1 2 3} FV -?– неизвестна конечная накопленная сумма

R R R R

FV= R*S_t

R- величина единичного платежа.

- это коэффициент будущей стоимости аннуитета (2 фактор).

Пример:

Ежегодно (в конце года) на специальный амортизационный счет в банке вносится по 1 млн. руб. в течении 3-х лет под 10% годовых. Какая сумма будет на счету спустя 3 года?

FV₃ = R*S_{3, 10%}=1 млн. руб. *3,31 =3,31 млн. руб.

или

FV = 1* =1*3,31 = 3,31 млн. руб.

3. Фактор фонда возмещения (3 колонка).

Используется для определения аннуитетных платежей или поступлений, которые необходимы в конце каждого момента времени в течение заданного периода, для того, чтобы к концу срока накопить на счете определенную сумму. Он является обратной величиной будущей стоимости аннуитета (2 фактору).

= – фактор фонда возмещения

FV=R*S_t

R= =FV*

 

Неизвестна сумма единичных платежей (R)

 

0 1 2 3 FV известна конечная накопленная сумма

R -? R-? R-? R-?

Пример:

Необходимо накопить за 5 лет 100 млн. руб. Есть возможность открыть счет под 10% годовых. Сколько нужно перечислять ежегодно, чтобы к концу 5 года собрать 100 млн. руб.?

R = FV₅ * =100 * 0,1637957=16,38 млн. руб.

(фактор фонда возмещения смотрим в таблице).

 

4. Фактор текущей стоимости денежной единицы (реверсия)

(колонка 4) это дисконтирование.

Это величина обратная накопленной сумме денежной единицы (1 фактору).

Показывает стоимость на данный момент той единицы, которая будет получена в будущем. Графически можно представить:

 

PV-? FV

t = 0 t

α_t = – фактор текущей стоимости денежной единицы (коэффициент дисконтирования)

Цель инвестирования – это получение дохода в будущем. Из этого следует, умножая коэффициент текущей стоимости (α_t) на ожидаемый будущий доход (FV) можно оценить текущую стоимость капиталовложения.

Здесь применяется метод дисконтирования.

PV = FV*

PV = FV* α_t

Рубль, полученный в будущем, стоит меньше сегодняшнего рубля (и не только из-за инфляции)

Пример:

Какова текущая стоимость суммы в 100 руб., которая будет получена через 5 лет, если процентная ставка равна 8%?

PV=FV* α_5;8% =100*0,6805=68,05 руб.

 

5. Фактор текущей стоимости обычного аннуитета или текущая стоимость единичного вложения по периодам (колонка5).

Используется для определения текущей стоимости (PV) потока равных аннуитетных платежей или поступлений, осуществляемых в конце каждого момента времени в течение заданного периода.

Графически можно представить:

PV -?

^{0 1 2 3}

R R R R – известны размеры аннуитетных платежей.

 

1-αt Е

a_t = = =

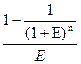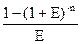a_t – текущая стоимость аннуитета

Пример.

Единичное вложение по 300 тыс.руб. выполняется раз в год в течении 2 лет. Какова текущая стоимость вложений, если расчетная процентная ставка 8 % в год.

Е = 8%, смотрим в таблице за 2 года (периода)

PV=R*a_2;8 =300000*1,783=534900 руб.

6. Фактор взноса на амортизацию единицы (коэффициент погашения долга в рассрочку или коэффициент периодического погашения) (колонка 6).

Используется для определения аннуитетных платежей, необходимых для того, чтобы к заданному сроку был полностью погашен кредит PV. Это величина обратная текущей стоимости обычного аннуитета (фактор 5).

Его называют методом времени возврата инвестиций.

Графически можно представить:

 

 

PV - известен

^{0 1 2 3}

1 аt

Е_ 1-αt

R -? R-? R -? R-? – неизвестны размеры аннуитетных платежей.

1 аt

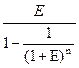= = – фактор взноса на амортизацию единицы.

R = PV*

Пример

 

Взяли кредит 500 тыс. руб. на 5 лет под 10% годовых. Чему равны ежегодные платежи по кредиту с учетом процентов?

 

R = 500*0,2638 = 131,9 тыс. руб.

 

131,9*5 лет = 659,5 тыс. руб.

 

Все шесть функций сложного процента строятся с использованием базовой формулы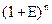

Базовые функции сложного процента и их обратные величины

Колонка таблицы	Прямая функция	Колонка таблицы	Обратная функция
	Накопленная сумма денежной единицы		Текущая стоимость денежной единицы
	Накопленные денежные единицы за период		Фактор фонда возмещения
	Текущая стоимость обычного аннуитета		Взнос на амортизацию единицы

 

Примеры для самостоятельной работы по сложным %.

Пример.

Ежегодные денежные поступления в сумме 500т.р. 5 лет под 15% годовых.

Какая сумма будет через 5 лет.

 

 

Пример.

Какая денежная сумма д.б. положена в банк, чтобы её покупательная способность спустя 3 года составила 500 т.р., если банковский %=10% годовых.

 

 

Пример.

Какая будет стоимость капитала в 800 т.р. через 9 лет, если он даёт 10% годового дохода.

Пример.

Сколько необходимо перечислять ежегодно чтобы накопить за 3 года 200 т.р. под 12% годовых

Пример.

Взяли кредит 1 млн. руб. на 5 лет под 11% годовых.

Сколько нужно вносить ежегодно для погашения.

 

 

Пример.

Ежегодно в течении 5 лет вкладывается по 200 т.р. под 14% годовых. Найти текущую стоимость вложений.