Решение показательных и логарифмических неравенств
Показательные неравенства – это неравенства, содержащие переменные
в показателе степени. Простейшее показательное неравенство имеет вид
a x > b или a x < b, где a > 0 или a ¹1. При решении показательных неравенств
необходимо помнить, что показательная функция y = a x возрастает при a >1
и убывает при 0 < a <1.
а) если а >1, то неравенство а х > а у равносильно неравенству х > у.
б) если 0 < а <1, то неравенство а х > а у равносильно неравенству х < у.
Применение монотонности функции.
Решение простейших показательных неравенств вида
и
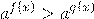
основывается на свойстве показательной функции
которая возрастает при a>1 и убывает при 0<a<1.
Рассмотрим решение простейших показательных неравенств на конкретных примерах.
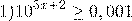
Приводим обе части неравенства к степеням с одинаковым основанием.
Так как 10>1, показательная функция
возрастает, знак неравенства между показателями степеней не изменяется:
Это — линейное неравенство. Алгоритм решения: неизвестные — в одну сторону, известные — в другую с противоположным знаком:
Обе части неравенства делим на число, стоящее перед иксом. При делении на положительное число знак неравенства не меняется:
Полученное решение изобразим на числовой прямой. Так как неравенство нестрогое, -1 отмечаем закрашенной точкой:
Ответ: [-1; ∞).
Приводим обе части неравенства к степеням с одинаковым основанием:
Так как основание 0,3<1, показательная функция
убывает, знак неравенства между показателями степеней изменяется на противоположный:
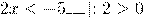
Изобразим решение неравенства на числовой прямой. Так как неравенство строгое, -2,5 отмечается выколотой точкой:
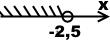
Ответ: (-∞; -2,5).
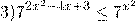
Так как основание 7>1, показательная функция возрастает, знак неравенства между показателями не меняется:
Это неравенство — квадратичное. Решим его методом интервалов.
Ищем нули функции y=x²-4x+3, то есть решаем квадратное уравнение
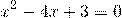
Полученные корни x1=1, x2=3 отмечаем на числовой прямой (закрашенными точками, так как неравенство нестрогое):
Ответ: [1; 3].
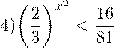
Приводим обе части к степеням с одинаковым основанием
Так как основание 2/3 меньше единицы, показательная функция убывает, поэтому знак неравенства между показателями степеней изменяется на противоположный:
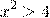
Получили квадратичное неравенство. Решим его методом интервалов.
Решение неравенства отметим на числовой прямой:
Ответ: (-∞; -2)U(2; ∞).
логарифмические неравенства
Для 
график логарифмической функции выглядит следующим образом:
- возрастающая функция: чем больше 
, тем больше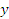 
Для 
график логарифмической функции выглядит следующим образом:
- убывающая функция: чем больше , тем меньше
Лучше всего начинать решение неравенств с проверки ОДЗ. Поскольку даже на первом шаге решения можно получить выражение с измененной ОДЗ.
Например:
Решить неравенство:
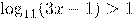
ОДЗ:
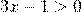
Решение:
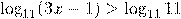
Так как основание логарифма больше 1, то знак неравенства сохраняем:
Ответ: 
2.Решить неравенство:
ОДЗ:
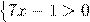
Решение:
Так как основание логарифма меньше 1, то знак неравенства меняем:
Пересекаем решение и ОДЗ, имеем: 
.Решить неравенство:
ОДЗ:
Решение этой системы – 
Решение:
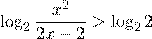
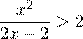
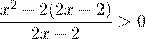
Точка 1 является выколотой – это корень знаменателя, точка 2 – корень четной кратности, а мы помним, что в таких точках знак интервала не изменяется! Поэтому решение будет выглядеть так:
Решение неравенства
Решение неравенства:
Это полностью укладывается в ОДЗ, поэтому ответ таким и будет:
Ответ: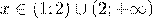 
Решите неравенства
1.45-2x<0,25.
2. 0,42х+1≥0,16.
3.23-x+21-x>40
4. 
5. 
