Каждый студент должен решить либо по две задачи из групп A, Б и одну – из группы В, либо одну задачу из группы В и одну задачу из группы Г. Привести блок-схемы решения задач из групп Б и Г соответственно.
А
1. Даны три действительные числа. Возвести в квадрат те из них, значения которых неотрицательны, и в четвертую степень — отрицательные.
2. Даны две точки А(x1, y1) и В(x2, y2). Составить алгоритм, определяющий, которая из точек находится ближе к началу координат.
3. Даны два угла треугольника (в градусах). Определить, существует ли такой треугольник. Если да, то будет ли он прямоугольным.
4. Даны действительные числа x и y, не равные друг другу. Меньшее из этих двух чисел заменить половиной их суммы, а большее — их удвоенным произведением.
5. На плоскости XOY задана своими координатами точка А. Указать, где она расположена: на какой оси или в каком координатном угле.
6. Даны целые числа m, n. Если числа не равны, то заменить каждое из них одним и тем же числом, равным большему из исходных, а если равны, то заменить числа нулями.
7. Дано трехзначное число N. Проверить, будет ли сумма его цифр четным числом.
8. Определить, равен ли квадрат заданного трехзначного числа кубу суммы цифр этого числа.
9. Определить, является ли целое число N четным двузначным числом.
10. Определить, является ли треугольник со сторонами a, b, c равносторонним.
11. Определить, является ли треугольник со сторонами a, b, c равнобедренным.
12. Определить, имеется ли среди чисел a, b, c хотя бы одна пара взаимно противоположных чисел.
13. Подсчитать количество отрицательных чисел среди чисел a, b, c.
14. Подсчитать количество положительных чисел среди чисел a, b, c.
15. Подсчитать количество целых чисел среди чисел a, b, c.
16. Определить, делителем каких из чисел a, b, c является число k.
17. Услуги телефонной сети оплачиваются по следующему правилу: за разговоры до А минут в месяц оплачиваются В р., а разговоры сверх установленной нормы оплачиваются из расчета С р. в минуту. Написать программу, вычисляющую плату за пользование телефоном для введенного времени разговоров за месяц.
18. Даны три стороны одного и три стороны другого треугольника. Определить, будут ли эти треугольники равновеликими, т.е. имеют ли они равные площади.
19. Программа-льстец. На экране появляется вопрос “Какой ты: высокий или невысокий? Введи В или Н”. В зависимости от ответа на экране должен появиться текст “Мне нравятся высокие люди!” или “Мне нравятся невысокие люди!”.
20. Грузовой автомобиль выехал из одного города в другой со скоростью v1 км/ч. Через t ч в этом же направлении выехал легковой автомобиль со скоростью v2 км/ч. Составить программу, определяющую, догонит ли легковой автомобиль грузовой через n ч после своего выезда.
21. Перераспределить значения переменных x и y так, чтобы в xоказалось большее из этих значений, а в y — меньшее.
22. Определить правильность даты, введенной с клавиатуры (число — от 1 до 31, месяц — от 1 до 12). Если введены некорректные данные, то сообщить об этом.
23. Составить программу, определяющую результат гадания на ромашке — “любит — не любит”, взяв за исходное данное количество лепестков n.
Б
1. Написать программу нахождения суммы большего и меньшего из 3 чисел.
2. Написать программу, определяющую по длинам сторон треугольника, является ли он прямоугольным. Если треугольник не прямоугольный, то вычислить косинус угла, лежащего против большей стороны.
3. Найти max{min{a, b}, min{c, d}}.
4. Даны три числа а, b, с. Определить, какое из них равно d. Если ни одно не равно d, то найти max{d-a, d-b, d-c}.
5. Даны четыре точки А1(x1, y1 ), A2(x2, y2), А3(x3, y3), А4(x4, y4). Определить, будут ли они вершинами параллелограмма.
6. Даны три точки А (x1, y1), B(x2, y2), C(x3, y3). Определить, будут ли они расположены на одной прямой. Если нет, то вычислить периметр треугольника ABC.
7. Даны действительные числа а, b, с. Удвоить эти числа, если а<b<с, и заменить их абсолютными значениями, если это не так.
8. На оси ОХ расположены три точки а, b, с. Определить, какая из точек b,c расположена ближе к а.
9. Даны три положительных числа а, b, с. Проверить, могут ли они быть длинами сторон треугольника. Если да, то вычислить площадь этого треугольника.
10. Написать программу решения уравнения ax3 + bх = 0 для произвольных а, b.
11. Дан круг радиуса R. Определить, поместится ли правильный треугольник со стороной а в этом круге.
12. Даны числа x, y, z. Найти значение выражения:
13. Дано число x. Напечатать в порядке возрастания числа: sinx, cosx. lnx. Если при каком-либо x некоторые из выражений не имеют смысла, вывести сообщение об этом и сравнивать значения только тех, которые имеют смысл.
14. Заданы размеры A, B прямоугольного отверстия и размеры X, Y, Z кирпича. Определить, пройдет ли кирпич через отверстие.
15. Составить программу, осуществляющую перевод величин из радианной меры в градусную или наоборот. Программа должна запрашивать, какой перевод нужно осуществить, и выполнять указанное действие.
16. Два прямоугольника, расположенные в первом квадранте, со сторонами, параллельными осям координат, заданы координатами своих левого верхнего и правого нижнего углов. Для первого прямоугольника это точки (x1, y1) и(x2, 0), для второго — (x3, y3), (x4, 0) Составить программу, определяющую, пересекаются ли данные прямоугольники, и вычисляющую площадь общей части, если они пересекаются.
17. В небоскребе N этажей и всего один подъезд; на каждом этаже по 3 квартиры; лифт может останавливаться только на нечетных этажах. Человек садится в лифт и набирает номер нужной ему квартиры М. На какой этаж должен доставить лифт пассажира?
18. Написать программу, которая по заданным трем числам определяет, является ли сумма каких-либо двух из них положительной.
19. Известно, что из четырех чисел a1, a2, a3 и a4 одно отлично от трех других, равных между собой; присвоить номер этого числа переменной n.
20. Составить программу, которая проверяла бы, не приводит ли суммирование двух целых чисел А и В к переполнению (т.е. к результату большему, чем 32767). Если будет переполнение, то сообщить об этом, иначе вывести сумму этих чисел.
В
Для данного x вычислить значение функции:
1. 
| 2.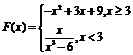 
|
3. 
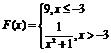
| 4. 
|
5.  
| 6. 
|
7. 
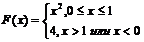
| 8. 
|
9. 
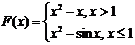
| 10.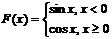 
|
11. 
| 12.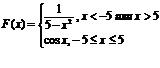 
|
Г
1. Даны действительные числа a, b, c(a > 0). Полностью исследовать биквадратное уравнение ax4 + bх2 + с = 0, т.е. если действительных корней нет, то должно быть выдано сообщение об этом, иначе найти действительные корни, сообщив, сколько из них являются различными.
2. Дана точка А(х, у). Определить, принадлежит ли она треугольнику с вершинами в точках (x1, y1), (x2, y2), (x3, y3).
3. Написать программу, определяющую, будут ли прямые А1х + В1у + С = 0 и А2х + В2у + С = 0 перпендикулярны. Если нет, то найти угол между ними.
4. Если сумма трех попарно различных действительных чисел X, Y, Z меньше единицы, то наименьшее из этих трех чисел заменить полусуммой двух других; в противном случае заменить меньшее из X, Y полусуммой двух оставшихся значений.
5. 
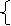Написать программу решения системы линейных уравнений
a1x + b1y = c1
a2x + b2y = c2
6. Даны три положительных числа. Определить, можно ли построить треугольник с длинами сторон, равным этим числам. Если можно, то ответить на вопрос, является ли он остроугольным.
7. Найти координаты точек пересечения прямой y = kx + b и окружности радиуса R с центром в начале координат. В каких координатных четвертях находятся точки пересечения? Если точек пересечения нет или прямая касается окружности, выдать соответствующее сообщение.
8. Заданы координаты вершин прямоугольника: (x1, y1), (x2, y2), (x3, y3), (x4, y4). Определить площадь части прямоугольника, расположенной в I-й координатной четверти.