Задача 5.1 На трех складах (I, II, III) имеются соответственно 90, 70, 50 тонн муки, которую надо перевезти в магазины (1, 2, 3, 4) соответственно в количестве 80, 60, 40, 30 тонн. Необходимо составить оптимальный план перевозки муки, если стоимость перевозки 1 тонны в магазины 1, 2, 3, 4 со склада I равна соответственно 2, 1, 3, 2 рублям, со склада II — 2, 3, 3, 1 рублям, со склада III —3, 3, 2, 1 рублям.
На основании приведенного экономического описания сформулируем эту задачу математически, т.е. построим ее математическую модель. Представим условие этой задачи в виде таблицы 5.1.
Через хij обозначим количество муки в тоннах, перевозимое с i -ro склада в j -ый магазин. Так, х23 - количество муки, перевозимое со склада II в 3 магазин, х12 — со склада I в магазин 2 и т. д.
Количество муки, вывозимое со склада I в магазины, таково:
Эта сумма равна 90, так как со склада I вывозится вся мука.
.
Аналогично для складов II и III имеем;
Таблица 5.1
 Магазин
Склады
| Отправлено тонн муки | ||||||||||||
| I | |||||||||||||
| II | |||||||||||||
| III | |||||||||||||
| Получено тонн муки |
Так как потребность каждого из магазинов по условию задачи полностью удовлетворяется количеством муки, полученной со складов I, II, III, то:
Естественно считать, что значения переменных xij - неотрицательны (иначе имели бы какой-то смысл обратные перевозки). Итак, переменные xij где i = 1,2,3, а j = 1,2,3,4, удовлетворяют следующей системе уравнений и неравенств:
(5.1.1)
Система (5.1.1) называется системой ограничений данной задачи. Обозначив через F все транспортные расходы, имеем:
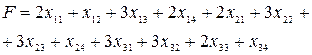(5.1.2)
Функция F называется целевой функцией. Каждое решение системы (5.1.1) является одним из возможных вариантов решения. Каждое такое решение носит название допустимого плана. Задача линейного программирования состоит в отыскании на множестве допустимых планов такого плана, который обращал бы в минимум целевую функцию F. Такой допустимый план называют оптимальным.
Сформулируем теперь задачу математически:
на множестве решений системы ограничений (5.1.1) найти такое, которое обращает в минимум целевую функцию (5.1.2), или: найти оптимальный план, определяемый системой ограничений (5.1.1) и целевой функцией (5.1.2).
Задача, которую мы рассмотрели, может быть представлена и в общем виде, т.е. с любым числом поставщиков и потребителей. Задачи такого типа называют транспортными задачами по критерию стоимости.
Математическая модель транспортной задачи имеет некоторые
особенности. В рассмотренной задаче общее наличие груза
у поставщиков (210 т) равно общей потребности получателей
(210 т). Такая модель называется закрытой моделью, а соответствующая ей транспортная задача называется сбалансированной
транспортной задачей.
В экономических расчетах широкое распространение получили и так называемые открытые модели, в которых указанное равенство не соблюдается. При этом возможны два случая: или запас у поставщиков больше, чем потребности покупателей, или, наоборот, спрос превышает наличие грузов. Заметим, что открытые модели можно сводить к закрытым.
Система ограничений (5.1.1) содержит 7 уравнений с 12 переменными. Любое из них можно отбросить, так как оно вытекает из остальных шести. Например, последнее уравнение можно получить, если сложить почленно первые три уравнения и от полученного уравнения отнять уравнения 4,5 и 6:
Это следует из того, что если определено наличие груза у всех отправителей и потребность всех получателей, кроме одного, то спрос последнего легко установить как разность между общим запасом и общей потребностью оставшихся получателей. Этот вывод справедлив для любой сбалансированной транспортной задачи: если m- число поставщиков, п -число получателей, то система ограничений содержит 
независимых уравнений с тп переменными.
Теперь рассмотрим несбалансированную транспортную задачу.
Задача 5.2 В пунктах А и В расположены кирпичные заводы, а в пунктах С и D —карьеры, снабжающие их песком. Потребность заводов в песке не больше производительности карьеров. Известно, сколько песка надо каждому из заводов и сколько его добывают в каждом из карьеров. Известна также стоимость перевозки 1 тонны песка из каждого карьера к заводам. Как спланировать снабжение заводов песком, чтобы затраты были наименьшими? (Все необходимые по задаче данные приведены на рисунке 5.1 )
Построим математическую модель этой задачи. Потребность заводов в песке (90 т) меньше производительности карьеров (100 т). Обозначим через х11 количество песка в тоннах, перевозимого из карьера С на завод А, через х12 — из С на В, через х21 – из D на А, x 22 —из D на В.
На завод А надо привезти 40 т песка:
На завод В должно быть доставлено 50 т песка:
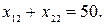
Из карьера D может быть вывезено не более 30 т песка:
Из карьера С может быть вывезено не более 70 т песка:
Стоимость всех перевозок определяется целевой функцией:
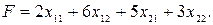(5.2.1)
Получаем математическую формулировку задачи. На множестве решений системы ограничений:
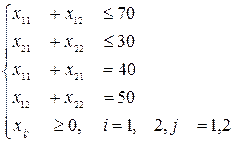(5.2.2)
надо найти такое решение, которое минимизировало бы целевую функцию (5.2.1.).
Следует заметить, что в систему ограничений несбалансированной транспортной задачи входят наряду с уравнениями также и неравенства.