Опишем теперь рассмотренный на частных примерах алгоритм в общем случае.
Основные этапы решения сбалансированной транспортной задачи.
I. Построение математической модели данной
задачи.
II. Применение алгоритма метода решения
транспортной задачи.
1) Составление задачи, двойственной данной.
2) Определение первоначального плана перевозок. Для этого используется правило «северо-западного угла». После заполнения максимально возможным количеством груза северо-западной клетки (верхняя левая) - переходим к заполнению соседней клетки. Ею может оказаться или соседняя по строке, или соседняя по столбцу, в зависимости от того, где имеются еще не использованные возможности для перевозок. Этот процесс продолжается до распределения всего количества груза. Как правило, число всех заполненных клеток есть  , где т — число поставщиков, п — число покупателей. Однако следует иметь в виду, что возможны так называемые случаи вырождения, когда число заполненных клеток не равно
, где т — число поставщиков, п — число покупателей. Однако следует иметь в виду, что возможны так называемые случаи вырождения, когда число заполненных клеток не равно  . Этим мы займемся в следующем параграфе.
. Этим мы займемся в следующем параграфе.
3) Проверка полученного плана на оптимальность.
Исходя из того, что если некоторые переменные исходной задачи строго больше нуля, то соответствующие им условия двойственной задачи выполняются как строгие равенства, получаем систему  уравнений с
уравнений с  переменными:
переменными: 
Найдем одно из решений этой системы и подставим его в остальные неравенства системы ограничений двойственной задачи, не вошедшие в систему  уравнений. Если все эти неравенства выполняются (т.е. являются верными), то проверяемый план является оптимальным. Если часть неравенств является неверными, то возможно дальнейшее улучшение плана.
уравнений. Если все эти неравенства выполняются (т.е. являются верными), то проверяемый план является оптимальным. Если часть неравенств является неверными, то возможно дальнейшее улучшение плана.
4) Переход к новому плану перевозок.
Вневерных неравенствах все члены переносим в правую часть. Выбираем неравенство (а вместе с ним и соответствующую ему переменную исходной задачи), у которого правая часть имеет наименьшее значение. При этом выборе свободная клетка таблицы распределения, соответствующая этой переменной, оказывается наиболее перспективной из всех имеющихся свободных клеток "для улучшения плана.
Для "выбранной клетки строим многоугольник и производим перемещение грузов в пределах клеток, связанных многоугольником с данной свободной клеткой. В выбранную свободную клетку записываем наименьшее из чисел, стоящих в клетках с отрицательными знаками. Это число, соответствующее количеству грузов, прибавляется к перевозкам всех клеток с положительными знаками и вычитается из всех клеток с отрицательными знаками. Остальные занятые клетки, не вошедшие в контур, остаются без изменения.
5) Проверка вновь полученного плана на оптимальность.
Далее все рассмотренные этапы повторяются в том же порядке до тех пор, пока не будет получен оптимальный план или выяснится, что данная задача не имеет оптимального решения.
III. Экономическая интерпретация полученного математического решения.
7. Составление первоначального опорного плана
| ПН ПО | V1 | V2 | … | Vn | запасы |
| U1 | с11 | c21 | … | с1n | a1 |
| U2 | c21 | c22 | … | с2n | a2 |
| … | … | … | … | … | … |
| Um | сm1 | cm2 | … | сmn | am |
| потребности | b1 | b2 | … | bn |
Решение транспортной задачи состоит из следующих этапов.
1. Определить модель транспортной задачи. Открытую модель
привести к закрытой.
Транспортная задача, в которой суммарные запасы и потребности совпадают, т. е. выполняется условие  , называется закрытой; в противном случае - открытой.
, называется закрытой; в противном случае - открытой.
Для открытой задачи возможны два случая:
1) суммарные запасы превышают суммарные потребности ( ). Тогда вводится фиктивный (n +1)-й пункт назначения с потребностью
). Тогда вводится фиктивный (n +1)-й пункт назначения с потребностью  ; со стоимостью перевозок единицы груза
; со стоимостью перевозок единицы груза  .
.
2) суммарные потребности превышают суммарные запасы ( ). Тогда вводится фиктивный (
). Тогда вводится фиктивный ( )-й пункт отправления с запасом груза am+1 =
)-й пункт отправления с запасом груза am+1 =  , со стоимостью перевозок единицы груза
, со стоимостью перевозок единицы груза  .
.
2. Составить первоначальный опорный план.
При составлении первоначального плана число заполненных клеток должно быть равно  . Если число заполненных клеток меньше, то недостающее количество клеток считаем условно заполненными, вписывая в них нули (лучше в клетки, имеющие наименьшую стоимость ).
. Если число заполненных клеток меньше, то недостающее количество клеток считаем условно заполненными, вписывая в них нули (лучше в клетки, имеющие наименьшую стоимость ).
Для определения опорного плана существуют различные методы. Среди них - метод минимальной стоимости, метод северо-западного угла.
Метод минимальной стоимости заключается в том, что из всей таблицы выбирают наименьшую стоимость 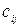 , и в клетку, которая ей соответствует, помещают
, и в клетку, которая ей соответствует, помещают 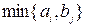 . Затем из рассмотрения исключают либо строку, соответствующую пункту отправления, запасы которого полностью израсходованы, либо столбец, соответствующий пункту назначения, потребности которого полностью удовлетворены. Из оставшейся части таблицы снова выбирают наименьшую стоимость и т. д. до тех пор, пока все запасы не будут распределены, а потребности удовлетворены.
. Затем из рассмотрения исключают либо строку, соответствующую пункту отправления, запасы которого полностью израсходованы, либо столбец, соответствующий пункту назначения, потребности которого полностью удовлетворены. Из оставшейся части таблицы снова выбирают наименьшую стоимость и т. д. до тех пор, пока все запасы не будут распределены, а потребности удовлетворены.
Пример: Составить опорный план транспортной задачи, заданной следующей распределительной таблицей
| V1 | V2 | V3 | V4 | |||
| U1 | |||||||
| U2 | |||||||
| U3 | |||||||
Решение: Наименьшая стоимость, равная 1, находится в клетке (1, 4). В нее помещаем груз  . Так как потребности пункта назначения V4 полностью удовлетворены, то из рассмотрения исключаем четвертый столбец. В оставшейся части таблицы наименьшая стоимость, равная 2, находится в клетке (1,2). В нее помещаем груз
. Так как потребности пункта назначения V4 полностью удовлетворены, то из рассмотрения исключаем четвертый столбец. В оставшейся части таблицы наименьшая стоимость, равная 2, находится в клетке (1,2). В нее помещаем груз  Так как запасы пункта отправления полностью израсходованы, то из рассмотрения исключаем первую строку. В оставшейся части таблицы наименьшей стоимостью является стоимость, расположенная в клетках (2, 1) и (3, 3). В клетку (2, 1) помещаем груз
Так как запасы пункта отправления полностью израсходованы, то из рассмотрения исключаем первую строку. В оставшейся части таблицы наименьшей стоимостью является стоимость, расположенная в клетках (2, 1) и (3, 3). В клетку (2, 1) помещаем груз  и исключаем из рассмотрения первый столбец V1. В клетку (3, 3) помещаем груз
и исключаем из рассмотрения первый столбец V1. В клетку (3, 3) помещаем груз  и исключаем из рассмотрения третий столбец V3. Остался только второй столбец V2, для которого
и исключаем из рассмотрения третий столбец V3. Остался только второй столбец V2, для которого  и
и  . В результате получили опорный план X:
. В результате получили опорный план X:

При данном плане перевозок общая стоимость перевозок составляет 
Метод северо-западного угла состоит в том, что заполнение таблицы начинается с левой верхней клетки для неизвестного х11. На каждом шаге рассматривается первый из оставшихся пунктов отправления и первый из оставшихся пунктов назначения. Составим опорный план уже рассмотренного примера.
Не учитывая стоимость перевозки единицы груза, заполнение таблицы начнем с клетки (1, 1). В нее вносим груз  . Так как потребности пункта назначения V1 полностью удовлетворены и запасы пункта отправления U1 полностью израсходованы, то из рассмотрения исключаем первый столбец и первую строку. Первым из оставшихся пунктов назначения является V2, а пунктом отправления -U2, поэтому далее заполняем клетку (2, 2). В нее помещаем х22 = min {a2, b2} = = min {250, 180} = 180 и исключаем из рассмотрения второй столбец V2. В клетку (2, 3) помещаем груз х23 = min {а2 - 180, b3} = = min {70, 100} = 70 и исключаем из рассмотрения вторую строку U2. Затем переходим к клетке (3, 3), в которую вносим груз х33 = min {а3, b3 - 70} = min {150, 30} = 30 и исключаем из рассмотрения третью строку U3.. Осталась одна свободная клетка (4, 4), которую заполняем, полагая, что
. Так как потребности пункта назначения V1 полностью удовлетворены и запасы пункта отправления U1 полностью израсходованы, то из рассмотрения исключаем первый столбец и первую строку. Первым из оставшихся пунктов назначения является V2, а пунктом отправления -U2, поэтому далее заполняем клетку (2, 2). В нее помещаем х22 = min {a2, b2} = = min {250, 180} = 180 и исключаем из рассмотрения второй столбец V2. В клетку (2, 3) помещаем груз х23 = min {а2 - 180, b3} = = min {70, 100} = 70 и исключаем из рассмотрения вторую строку U2. Затем переходим к клетке (3, 3), в которую вносим груз х33 = min {а3, b3 - 70} = min {150, 30} = 30 и исключаем из рассмотрения третью строку U3.. Осталась одна свободная клетка (4, 4), которую заполняем, полагая, что 
Однако, число заполненных клеток равно 5, а это меньше, чем  , поэтому одну клетку считаем условно заполненной, вписывая в нее 0 (взяли клетку (1, 4), так как она имеет наименьшую стоимость с14 = 1). В результате получили опорный план X:
, поэтому одну клетку считаем условно заполненной, вписывая в нее 0 (взяли клетку (1, 4), так как она имеет наименьшую стоимость с14 = 1). В результате получили опорный план X:

Согласно данному плану перевозок, общая стоимость перевозок составляет 
Заметим, что опорный план, составленный методом минимальной стоимости, ближе к оптимальному плану.