Задание для выполнения РГР №1
Дана схема электрической цепи с двумя источниками гармонических ЭДС: e 1(t) = E 1 m sin(314 t + ψ e 1) и e 2(t) = E 2 m sin(314 t + ψ e 2). Действующие значения и начальные фазы ЭДС приведены в табл.1.1. Заданы значения параметров элементов схемы (табл.1.2).
Требуется выполнить следующий объем расчетов:
1. Подсчитать комплексные сопротивления и проводимости ветвей. Индекс сопротивления равен индексу тока. Записать комплексы ЭДС источников. Составить комплексную схему замещения. На схеме должны быть указаны комплексные сопротивления, комплексы токов и ЭДС ветвей.
2. Определить токи в ветвях комплексной схемы замещения методом двух узлов. Осуществить проверку полученных результатов с помощью первого закона Кирхгофа.
3. Проверить выполнение баланса активных и реактивных мощностей. С этой целью подсчитать отдельно комплексные мощности источников и приемников энергии и сравнить их вещественные и мнимые части (т.е. активные и реактивные мощности). Погрешность расчета не должна превышать 2 %. Записать уравнение баланса мощностей с помощью матричного соотношения.
4. Собрать схему в программе Multisim с амперметрами и измерить действующие значения токов в ветвях.
Примечания.
1). Номер варианта задается трехзначным числом (три последние цифры номера зачетной книжки). Первая цифра этого числа – номер столбца в таблице 1.1, вторая цифра – номер строки в таблице 1.2, третья цифра – номер схемы.
2). Все расчеты, кроме решения узлового уравнения, должны быть выполнены с помощью инженерного калькулятора.
3). Все комплексы действующих значений ЭДС, напряжений и токов, комплексные сопротивления и проводимости должны быть записаны в двух формах – алгебраической и показательной.
Таблица 1.1 – Параметры источников ЭДС
| Варианты | ||||||||||
| E 1, В | ||||||||||
| ψ e 1, град | -30 | -20 | -40 | -60 | -70 | |||||
| E 2, В | ||||||||||
| ψ e 2, град | -40 | -60 | -35 | -55 | -75 |
Таблица 1.2 – Параметры пассивных двухполюсных элементов
| Варианты | L 1 Гн | L 2 Гн | C 1 мкФ | C 2 мкФ | R 1 Ом | R 2 Ом | R 3 Ом | R 4 Ом |
| 0,11 | 0,16 | |||||||
| 0,16 | 0,12 | |||||||
| 0,10 | 0,17 | |||||||
| 0,12 | 0,16 | |||||||
| 0,14 | 0,09 | |||||||
| 0,16 | 0,10 | |||||||
| 0,13 | 0,18 | |||||||
| 0,09 | 0,15 | |||||||
| 0,15 | 0,11 | |||||||
| 0,17 | 0,13 |
Пример выполнения РГР №1.
В пример включены два дополнительных пункта: 1). Расчет схемы МКТ; 2). Нахождение комплексных потенциалов точек схемы.
Исходные данные:
w = 314 рад/с; L 1 = 0,14 Гн; L 2 = 0.11 Гн; С 1 = 80 мкФ;
С 2 = 55 мкФ; R 1 = 20 Ом; R 2 = 35 Ом; R 3 = 22 Ом; R 4 = 40 Ом;
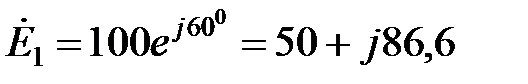 В;
В; 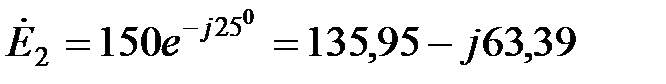 В.
В.
Рис. 1.1. Схема для мгновенных значений
Решение.
1. Подсчитать комплексные сопротивления ветвей. Индекс сопротивления равен индексу тока. Записать комплексы ЭДС источников. Составить комплексную схему замещения. На схеме должны быть указаны комплексные сопротивления, комплексы токов и ЭДС ветвей.
Сопротивления реактивных элементов:
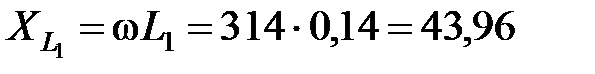 Ом;
Ом; 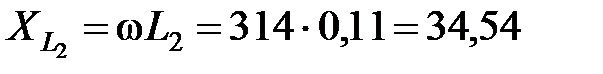 Ом;
Ом;
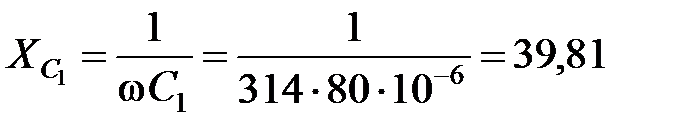 Ом;
Ом;
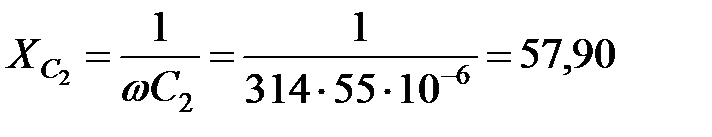 Ом.
Ом.
Комплексные сопротивления ветвей:
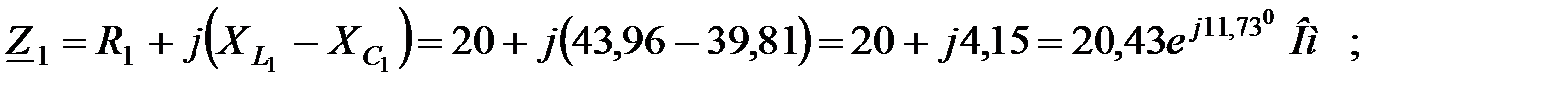
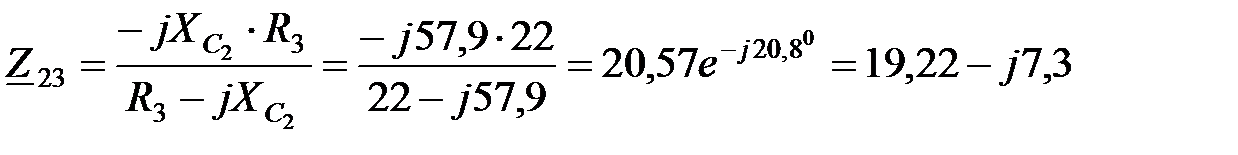 Ом;
Ом;
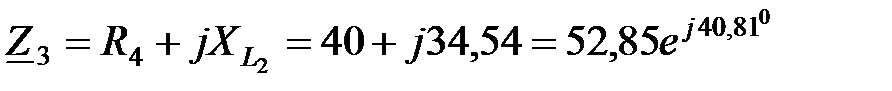 Ом.
Ом.
Рис. 1.2. Комплексная схема замещения
Объединим сопротивления во второй ветви:
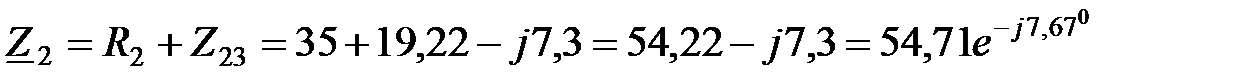 Ом;
Ом;
Рис. 1.3. Окончательнаясхема замещения
Комплексные проводимости ветвей:
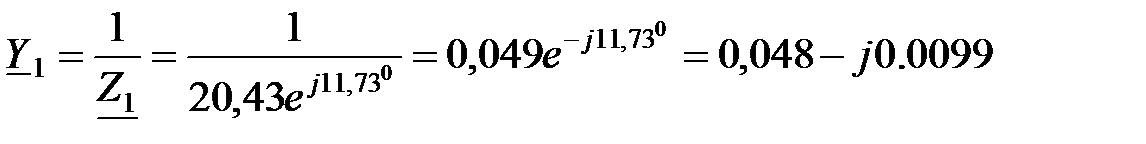 См;
См;
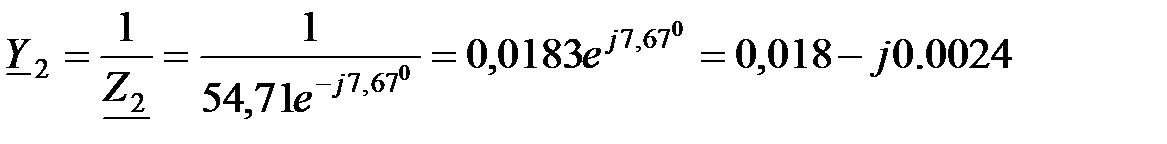 См;
См;
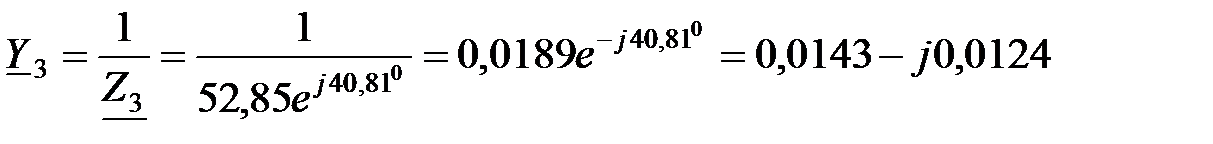 См.
См.
2. Определить токи в ветвях комплексной схемы замещения методом контурных токов. Осуществить проверку полученных результатов с помощью второго закона Кирхгофа.
Выбираем независимые контуры:
Рис. 1.4. Схема для расчета методом контурных токов
Составляем в общем виде (в канонической форме) систему контурных уравнений:
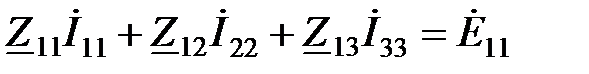 ;
;
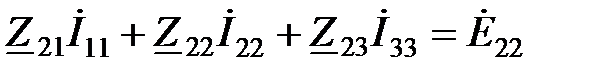 ;
;
Сопротивление с одинаковыми индексами Zi i называется собственным сопротивлением i -го контура и равно сумме сопротивлений всех ветвей, входящих в этот контур. Сопротивление с разными индексами Zij называется общим сопротивлением i -го и j -го контуров и равно сопротивлению ветви, общей для этих контуров. Общее сопротивление равно сопротивлению общей для этих контуров ветви, взятому со знаком плюс, если контурные токи рассматриваемых контуров протекают по общей ветви в одинаковом направлении. Если же контурные токи в общей ветви направлены в противоположные стороны, то общее сопротивление равно сопротивлению общей ветви, взятому со знаком минус. Правые части уравнений называются контурными ЭДС и представляют собой алгебраическую сумму ЭДС всех источников ЭДС, входящих в данный контур. Если направление ЭДС какого-либо источника, входящего в i -й контур, совпадает с направлением контурного тока этого контура, то соответствующая ЭДС входит в E ii со знаком плюс, в противном случае – со знаком минус.
Подсчитаем коэффициенты и правые части контурных уравнений приведенной схемы.
Собственные сопротивления контуров:
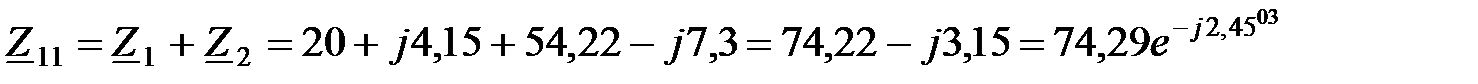 Ом;
Ом;
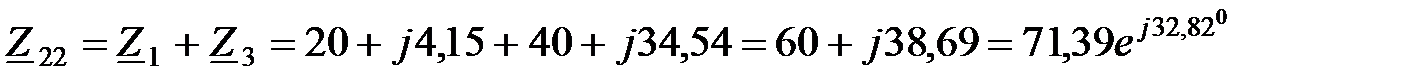 Ом.
Ом.
Общее сопротивление контуров:
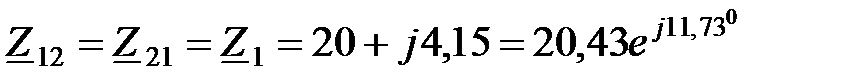 Ом.
Ом.
Контурные ЭДС:
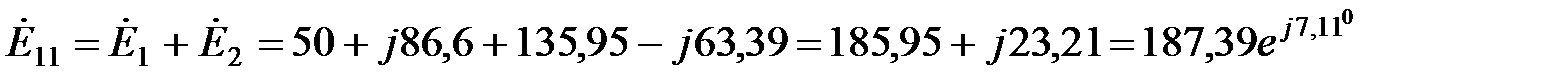 В;
В;
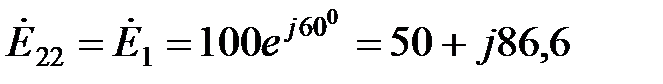 В.
В.
Решаем контурные уравнения в программе Mathcad.
Вводим комплексы контурных сопротивлений и ЭДС. Затем записываем матрицу-столбец искомых контурных токов, знак присваивания, квадратную матрицу контурных сопротивлений, возводим ее в степень (-1) для получения обратной матрицы и умножаем на матрицу-столбец контурных ЭДС. Ниже приведен фрагмент решения системы контурных уравнений:

Т.о., контурные токи в заданной схеме имеют значения:
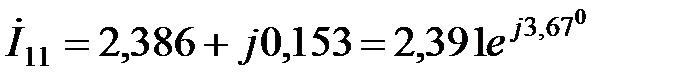 А;
А;
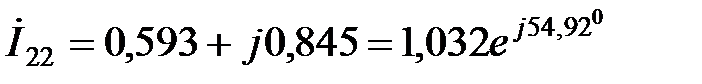 А;
А;
Токи в ветвях комплексной схемы:
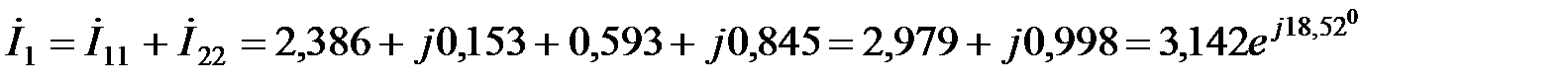 А;
А;
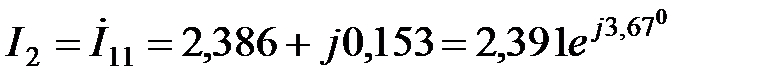 А;
А;
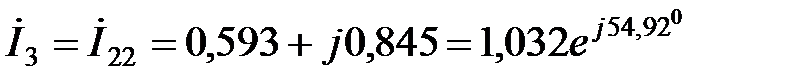 А.
А.
Комплексы напряжений на сопротивлениях комплексной схемы:
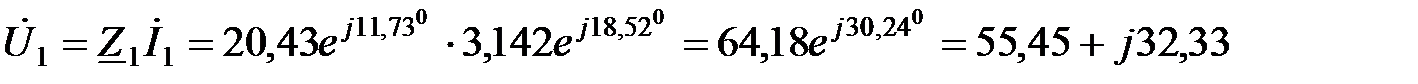 В;
В;
 В;
В;
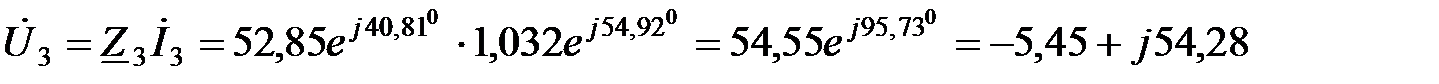 В.
В.
Проверка по второму закону Кирхгофа.
1).Первый контур:
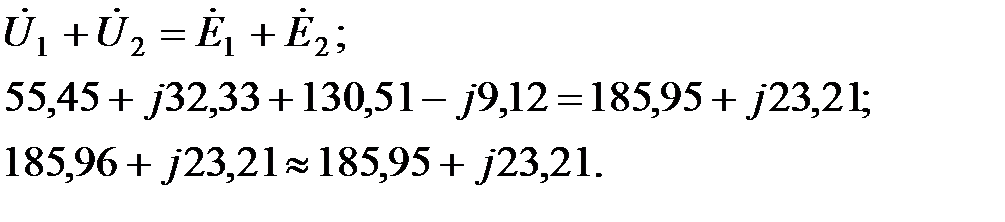
2). Второй контур:
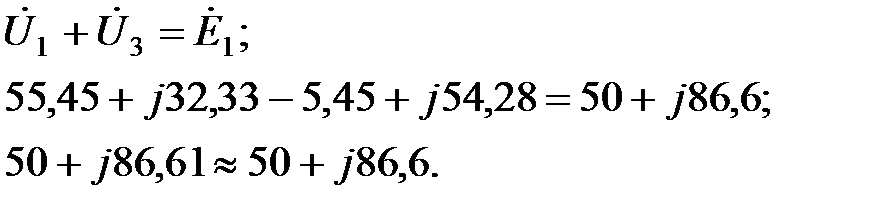
При проведении проверки сравниваются отдельно вещественные части и отдельно мнимые части левой и правой сторон тождества. Два комплексных числа равны тогда и только тогда, когда равны отдельно мнимые и вещественные части этих чисел. Если имеются отличия в значениях левой и правой частей, то нужно находить погрешность расчета в процентах: из большего модуля вычитается меньший, разность делится на больший модуль и умножается на 100%. Например, в уравнении для второго контура немного отличаются мнимые части. Найдем погрешность расчета:
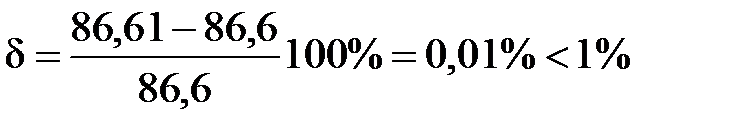 .
.
3. Определить токи в ветвях комплексной схемы замещения методом двух узлов. Осуществить проверку полученных результатов с помощью первого закона Кирхгофа.
При формировании уравнений электрического равновесия электрической цепи в качестве независимых переменных удобно использовать узловые напряжения, т.е. напряжения независимых узлов относительно базисного (опорного), который обычно обозначается цифрой 0. Узловые напряжения направлены от независимых узлов к базисному узлу и поэтому обозначаются через U 10, U 20, … Число узловых напряжений равно числу независимых узлов, т.е. на единицу меньше общего числа узлов. Поэтому в схеме с двумя узлами будет только одно узловое напряжение – напряжение между узлами схемы, и оно определяется по следующей формуле:
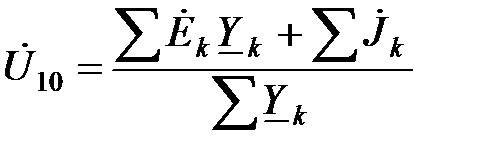 .
.
При подсчетах по этой формуле нужно учитывать следующие правила: если в какой-либо ветви схемы отсутствует ЭДС, то соответствующее слагаемое 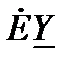 в числителе выпадает, но проводимость этой ветви в знаменателе остается; если ЭДС ветви направлена к независимому узлу (1), то слагаемое
в числителе выпадает, но проводимость этой ветви в знаменателе остается; если ЭДС ветви направлена к независимому узлу (1), то слагаемое 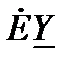 в числителе берется со знаком плюс, если ЭДС направлена от узла – то слагаемое
в числителе берется со знаком плюс, если ЭДС направлена от узла – то слагаемое 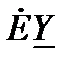 берется со знаком минус. То же правило относится к источникам тока, если они есть в схеме: если ток
берется со знаком минус. То же правило относится к источникам тока, если они есть в схеме: если ток 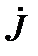 источника тока направлен к узлу (1), то этот ток в числителе берется со знаком плюс, если ток
источника тока направлен к узлу (1), то этот ток в числителе берется со знаком плюс, если ток 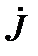 направлен от узла – то ток
направлен от узла – то ток 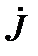 берется со знаком минус.
берется со знаком минус.
Укажем на схеме направление узлового напряжения:
Рис. 1.5. Схема для метода узловых напряжений
Напряжение между узлами схемы рис.1.5:
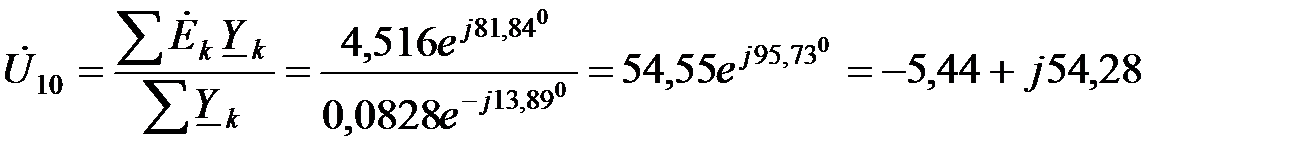 В.
В.
Здесь:
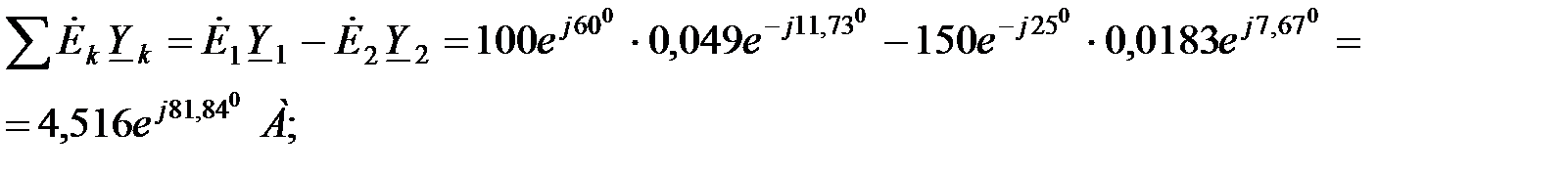
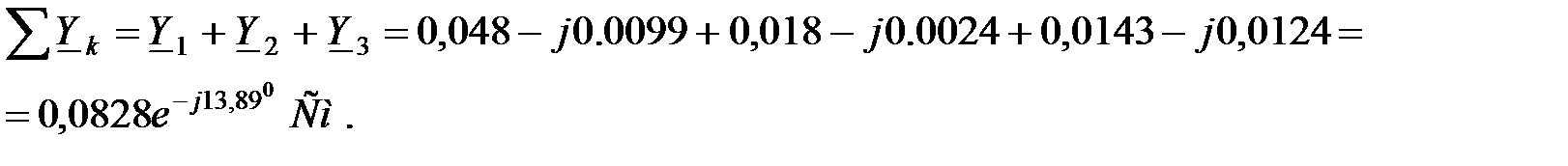
Токи в ветвях найдем по закону Ома для ветви с источником ЭДС:
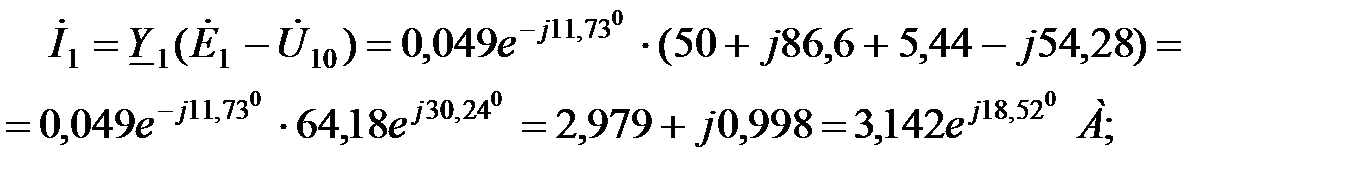 +
+
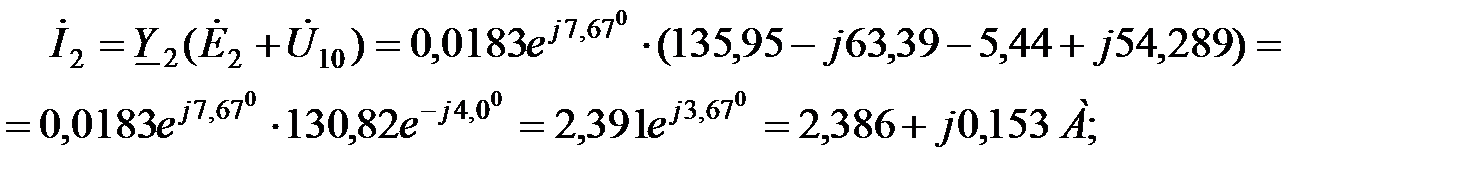 =
=
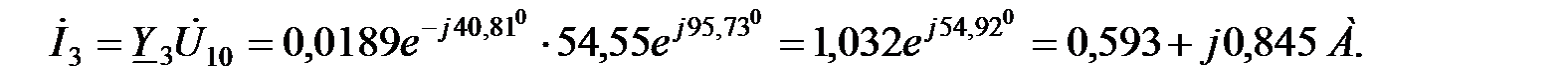
Проверка с помощью 1-го закона Кирхгофа.
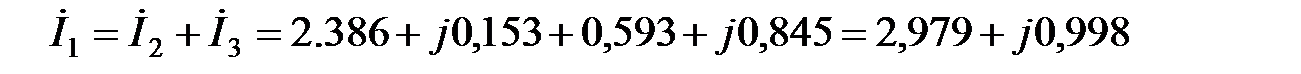 А.
А.
4. Проверить выполнение баланса активных и реактивных мощностей.
Комплексная мощность источника ЭДС находится как произведение комплекса ЭДС на сопряженный комплекс тока, и это произведение в сумме мощностей источников берется со знаком плюс, если ЭДС и ток ветви совпадают по направлению.
Комплексная, активная и реактивная мощности источников:
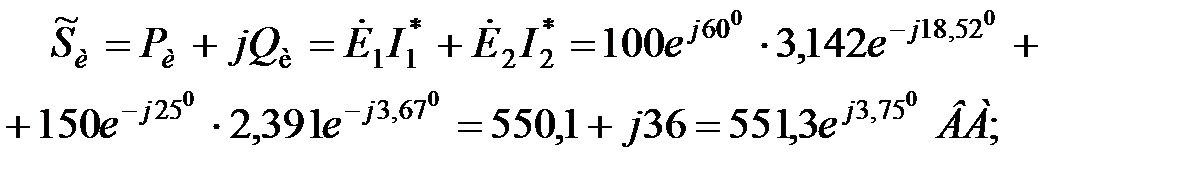
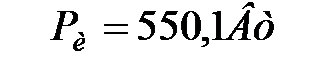 ;
; 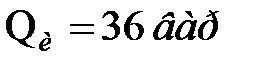 .
.
Комплексная, активная и реактивная мощности приемников:
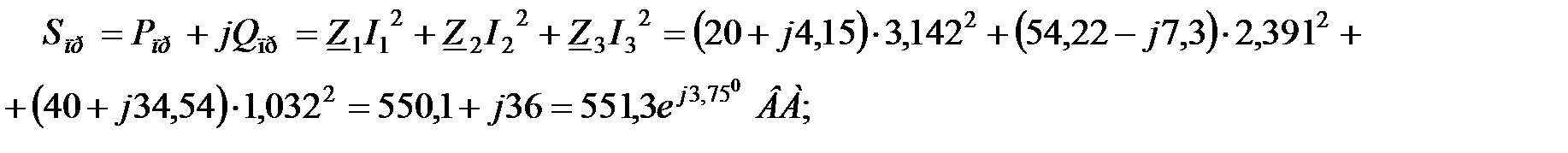
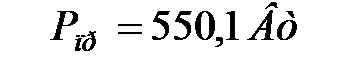 ;
; 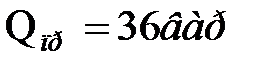 .
.
Вывод. В схеме имеет место баланс активных и реактивных мощностей, т.к. комплексная мощность источников энергии равна комплексной мощности приемников энергии.
5. Построить на комплексной плоскости векторную диаграмму комплексных потенциалов и векторную диаграмму токов в ветвях схемы.
Узлы схемы (устранимые и неустранимые) обозначим буквами:
Рис. 1.6. Схема для определения потенциалов узлов
Пусть комплексный потенциал узла 0 равен нулю:
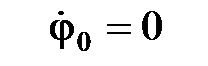 .
.
Найдем комплексные потенциалы остальных узлов схемы, учитывая, что ток течет от точки с большим потенциалом к точке с меньшим потенциалом, а ЭДС направлена от точки с меньшим потенциалом к точке с большим потенциалом:
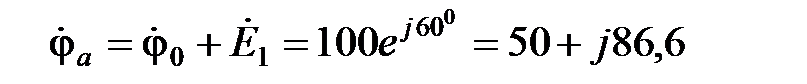 В;
В;
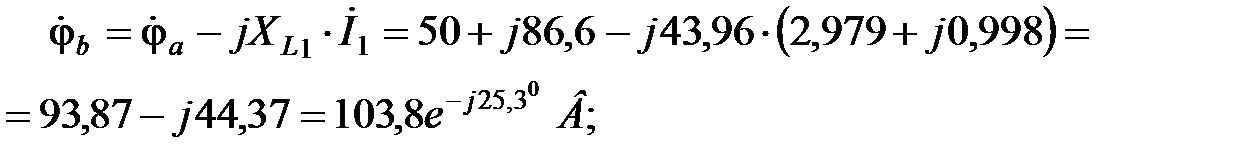
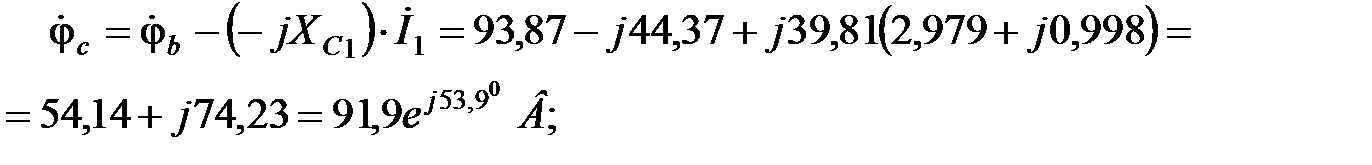
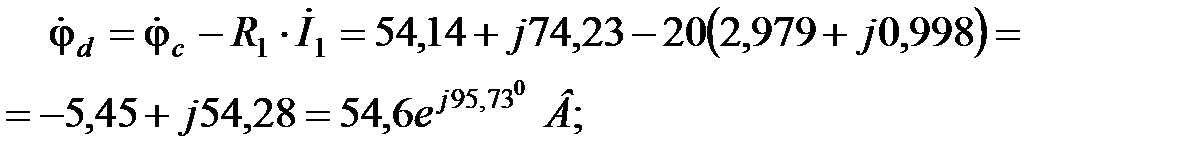
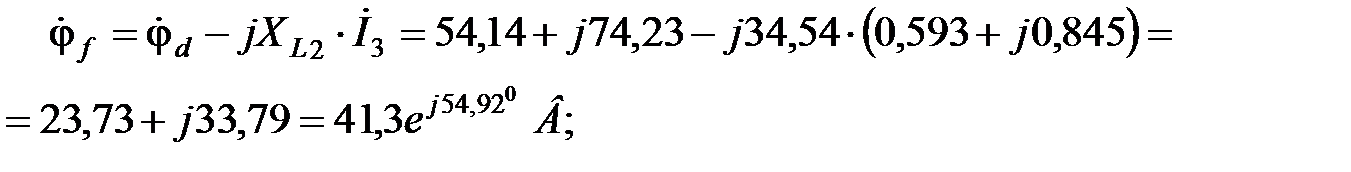
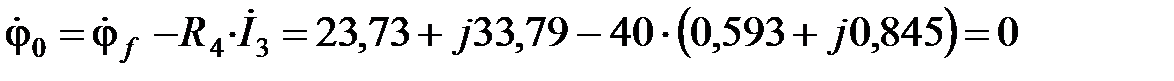 .
.
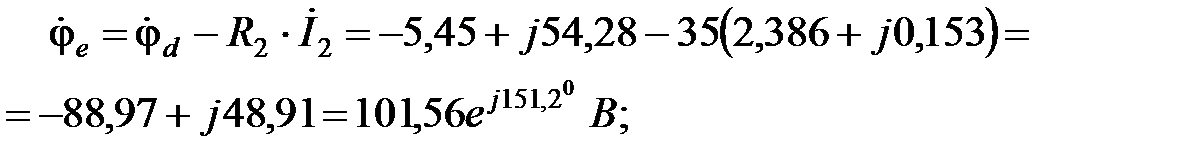
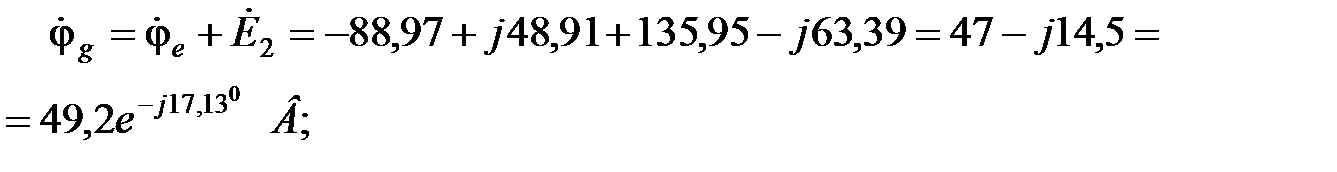
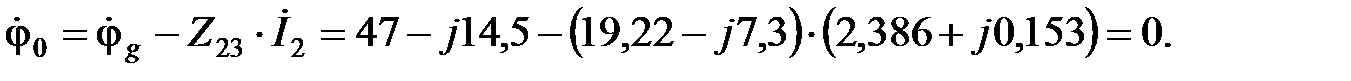
В этом пункте дважды подсчитывался потенциал базисного узла. Это делалось с целью проверки.
Далее строим на комплексной плоскости векторную диаграмму комплексных потенциалов и векторную диаграмму токов в ветвях схемы.
5. Собираем схему в программе Multisim с амперметрами и измеряем действующие значения токов в ветвях.
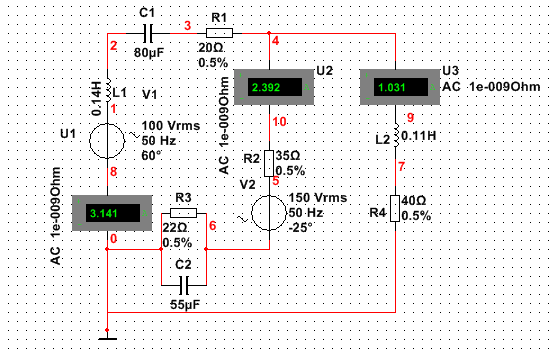
Рис. 1.7. Схема моделирования а Multisim
Вывод. Значения токов в ветвях, найденные расчетным путем и с помощью моделирования, практически совпадают.
РГР №2. Расчет трехфазных электрических цепей