1. Непрерывные (аналоговые) по информативному параметру и времени сигналы. Непрерывные сигналы определены в любой момент времени существования сигнала и могут принимать любые значения в диапазоне его измерения. В качестве таких сигналов нашли применения постоянные и гармонические токи и напряжения. Для постоянных токов i и напряжения u информационными параметрами являются их мгновенные значения, функционально связанные с измеряемой величиной x. На рис. 4-2, б изображен непрерывный сигнал y (ток i или напряжение u), связанный линейной зависимостью y=kx с измеряемой величиной x, здесь k — коэффициент преобразования (см. § 4-5).
В гармонических сигналах информативными параметрами могут быть амплитуда Ym, угловая частота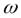 
или фаза 
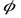. Измерение информативного параметра гармонического сигнала в соответствии с измеряемой величиной x называют модуляцией этого сигнала. Если с изменением x в гармоническом сигнале меняется один из параметром 
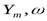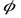или , то говорят, что осуществляется соответственно амплитудная – АМ (рис. 4-2, а, в), частотная – ЧМ (рис. 4-2, а, г) или фазовая – ФМ (рис. 4-2, а, д) модуляция. При фазовой модуляции фаза сигнала определяется, относительно второго (опорного) гармонического сигнала 
.
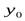2. Непрерывные по информационному параметру и дискретные по времени сигналы. Такие сигналы определяются на некотором конечном или счётном множестве моментов времени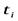 
(или на множестве интервалов времени 
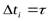, см. ниже). Теоретическая модель таких сигналов показана на рис. 4-2, е, где 
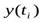- последовательность значений непрерывного сигнала y(t)=kx(t) (рис. 4-2, б), определённых в момент времени 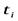. В реальных средствахизмерений подобным сигналом является периодическая последовательность импульсов постоянного тока (рис.4-2, ж), у которых в отличие от абстрактной модели, информативными параметрами могут быть не только амплитуда Ym, но и частота f и длительность т этих импульсов. При этом в зависимости от.того, какой из этих параметров функционально связан с х, имеет место соответственно амплитудно-импульсная — АИМ (рис. 4-2, а, ж),частотно-импульсная — ЧИМ (рис. 4-2, а, з) или широтно-импульсная — ШИМ (рис. 4-2, а, и) модуляция сигнала.
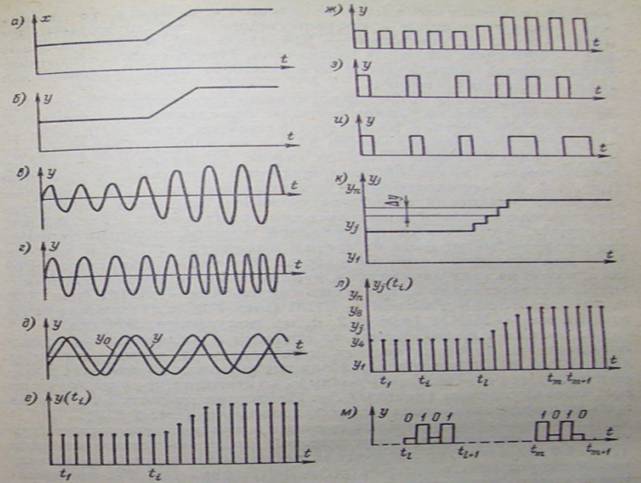
Рис. 4-2. Измеряемая величина х (а) и сигналы измерительной информации у (б — м)
3. Сигналы, непрерывные по времени и квантованные (дискретные) по информативному параметру. В таких сигналах (рис. 4-2, б, к) информативный параметр может принимать только некоторые разрешенные уровни у/, отстоящие друг от друга на конечные интервалы (кванты)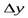 
. Примером является сигнал на выходе цифро-аналогового преобразователя (см. § 8-3).
4. Сигналы, дискретные по времени и квантованные по информативному параметру. Теоретической моделью такого сигнала (рис 4-2, л) является дискретная последовательность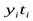 
значений неприрывного сигнала (Рис. 4-2, б), принимающая только разрешённые уровни 
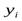, и определенная в дискретные моменты времени 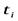. Такому виду сигналов соответствует, например, сигналы при кодово-импульсной модуляции, при которой в моменты времени 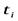каждому разрешенному уровню 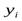ставится в соответствие определённый код – комбинация условных сигналов (см. п. 1-1, 8-1), в частности импульсов постоянного тока высокого уровня, обозначаемых 1, и импульсов низкого уровня, обозначаемых 0. Так, на рис. 4-2, м показаны две кодовые комбинации – 0101 и 1010, соответствующие уровням 
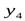и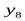 
(рис. 4-2, л) в моменты времен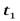и 
и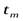 
.
Приведенные примеры сигналов широко используются в электрических средствах измерений. Однако следует иметь в виду, что находят применения и другие сигналы.
Для описания реальных физических сигналов применяют различные математические модели.
Математические модели сигналов. Под математической моделью понимают описание сигнала на формальном языке математики, т. е. с помощью формул, неравенств или логических соотношений. Для описания одних и тех же сигналов могут быть использованы различные математические модели. Выбор модели определяется адекватностью модели реальному сигналу, простотой математического описания, назначением модели и др.
Особенностью моделей сигналов измерительной информации является априорная (доопытная) неопределенность значений информативных параметров, обусловленная в общем случае неизвестными размерами измеряемых величин.
Существуют различные подходы к построению математических моделей сигналов.
1. Сигнал принимают квазидетерминированным. В этом случае для математического описания сигнала используют различные детерминированные функции времени. Модели таких сигналов называют квазидетерминированными (или детерминированными), подчеркивая тем самым, что вид функции, описывающей сигнал, известен, а неизвестными (информативными) являются ее параметры.
2. Сигнал рассматривают как случайный процесс. Описание таких сигналов основывается на теории вероятностей и теории случайных функций. В этом случае изменение сигнала во времени и пространстве характеризуется законом распределения, математическим ожиданием, дисперсией и корреляционной функцией. Модели' таких сигналов называют случайными.
3. Сигналы представляют в виде комбинации случайной и детерминированной составляющих, в частности в виде суммы сигнала измерительной информации (квазидетерминированная составляющая) и помехи (случайная составляющая).
Модели квазидетерминированных сигналов. При построении таких моделей используется как временное, так и спектральное представление сигналов. Во временной области применяют некоторые функции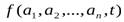 
, наиболее близко описывающие изменение сигнала во времени, в которых один из параметров 
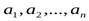, зависит от измеряемой величины x(t). Такими функциями могут быть: функция включения, дельта-функция, тригонометрические и экспоненциальная функции, различные алгебраические полиномы и др.
Рассмотрим некоторые примеры моделей квазидетерминированных сигналов.
А. При скачкообразном изменении измеряемой величины x(t) сигнал у(t) на выходе безынерционного измерительного преобразователя может быть записан с использованием функции включения.
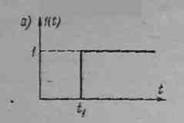
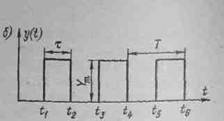
Рис. 4 - 3. Функция включения (а) и последовательность прямоугольных импульсов (б)
Функция включения (рис 4-3, а), или единичный скачок, определяется системой равенств
(4 -6)
С помощью этой функции сигнал измерительной информации может быть записан в виде
y(t)=a l(t-t 1) -kx (t) l(t-t1). (4 -7)
где k - коэффициент преобразования. Значение параметра а= kx(t) до опыта остается неизвестным, поэтому в рамках квазидетерминированной модели обычно оценивают диапазон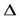 
а изменения сигнала в зависимости от диапазона ∆х изменения измеряемой величины.
Б. Использование детерминированных моделей особенно удобно при описании периодических сигналов. Так, уравнение амплитудно-модулированного гармонического сигнала (рис. 4 -2, в) имеет вид
Y(t) = Уm[l +тх t)]cos w0 t (4 - 8)
где w0 - частота так называемых несущих колебаний; т — коэффициент амплитудной модуляции, определяющий влияние х (t) на амплитуду Ym[l+mx(t)] синусоидальных колебаний. Диапазон изменения этой амплитуды характеризует глубину модуляции гармонического сигнала.
В. Для описания периодической последовательности прямоугольных импульсов постоянного тока (рис. 4 -3, б) применяют выражение
Y(t)=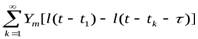 
(4 - 9)
где Ym — амплитуда импульса;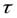 
— длительность импульса;T=tk+1-tk - период следования импульса. В этом случае аналитическое выражение для АИМ сигнала имеет вид
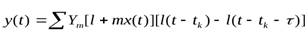(4 -10)
где m - коэффициент, характеризующий диапазон модуляции амплитуды Ym[l + mx (t)].
Выражения (4 - 8) и (4 - 10) описывают амплитудную модуляцию периодических сигналов. Аналогично могут быть получены аналитические зависимости для ЧМ, ФМ, ЧИМ и ШИМ, в которых соответствующие параметры модели являются функциями x(t).
Г. Сигналы измерительной информации могут иметь достаточно сложную структуру. Для точного описания таких сигналов (если оно принципиально возможно) приходится использовать сложные математические выражения. Часто оказывается удобным такие сигналы на интервале времени ∆t описывать суммой некоторых относительно простых функций (аппроксимировать суммой функций). В общем случае для точного описания сигнала необходимо использовать бесконечный ряд У( t) =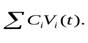 
Где Vi (t) - некоторые выбранные для аппроксимации функции {базисные функции); Ci - весовые коэффициенты. На практике используют конечную сумму аппроксимируемых функций.
у* (t) = 
, что приводит к погрешности аппроксимации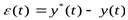 
, так как аппроксимирующая функция у* (t) не равна во всех точках у (t) (см. рис. 4 -6). Погрешность 
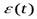зависит от вида функции и от интервала ∆t представления сигнала, т. е. интервала, на котором у(t) аппроксимируется у* (t). В качестве Vi (t) нашли применение полиномы Лагранжа (см. стр. 72), Лежандра, Чебышева и др.
Наряду с временным описанием сигналов широко используется их спектральное представление. Это представление основывается на преобразовании Фурье сигналов у (t). Применяя разложение в ряд Фурье, периодический сигнал у (t) может быть представлен суммой гармонических составляющих:
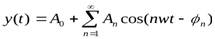(4 -11)
где Aо - постоянная составляющая; А nи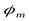 
- амплитуда и фазаn-й гармонической составляющей сигнала; n - номер гармони-ки. Множество значений А nи 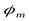образуют соответственно амплитудный и фазовый спектры сигнала. Такие спектры часто изображают графически.
Для непериодического сигнала у t /), используя интеграл Фурье, определяют его спектральную плотность
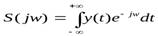(4 – 12)
Спектральное представление сигналов позволяет оценить частотный диапазон ∆ w, т.е. такой диапазон частот, в котором заключены все или основные (имеющие наибольшие амплитуды» гармонические составляющие сигнала.
Частотный диапазон является важной характеристикой сигналов, определяющей необходимую полосу пропускания средств измерении (см. § 4 - 6) для передачи сигналов с требуемой точностью. Так, для непрерывных сигналов у (t) при линейной зависимости у (t) =kx (t) вид спектра сигнала повторяет спектр измеряемой величины х (t) с точностью до постоянного множителя равного k. Следовательно, при таком сигнале средства измерений должны иметь полосу пропускания частот (см. § 4 -6), определяемую спектром измеряемой величины х (t).
При амплитудной модуляции гармонического сигнала спектр имеет более сложную зависимость от спектра входной величины х (t). Если х (t) представляет собой гармоническое колебание с частотой Ω, то на основании (4 - 8) и (4 - 11) получим
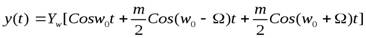Ω (4 - 13)
Спектр Аn такого сигнала показан на рис 4 - 4, а. Для неискаженной передачи этого сигнала средство измерений должно иметь полосу пропускания частот в диапазоне от w0 - Ω до w0+Ω,
При модуляции импульсных сигналов спектр имеет достаточно сложную структуру. В качестве примера на рис 4 - 4, б показав вид спектра АИМ сигнала при х (t) =cos Ωt.Спектр такого сигнала бесконечен по частоте. В этом случае при определении требований к полосе пропускания соответствующих средств измерений исходят из допускаемой погрешности искажения сигнала за счет ограничения его частотного диапазона. Приведенные примеры показывают важность анализа частотных характеристик (спектров) сигналов измерительной информации.
Таким образом, описание сигналов квазидетерминированными моделями дает хорошую математическую интерпретацию происходящих во времени процессов в средствах измерений. При известном х (t) эти модели дают точное (в пределах принятой модели) описание сигнала y{t). Однако поскольку измеряемая
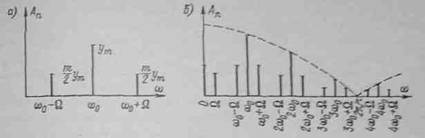Рис. 4-4. Спектры амплитудной (а) и амплитудно-импульсной (б) модуляции сигналов при гармоническом модулирующем сигнале
величина х (t) является неизвестной, то на основании этих моделей обычно определяют предельные' характеристики сигналов у (t): диапазон изменения сигнала и его информативного параметра, частотный диапазон и другие характеристики.
Модели случайных сигналов. Математические модели случайных сигналов основываются на использовании теории вероятностей и теории случайных процессов.
Во многих приложениях сигнал измерительной информации можно рассматривать как случайную величину. Например, последовательно измеряя сопротивления нескольких резисторов одного номинала, можно получить некоторый «разброс» в результатах измерений, обусловленный, в частности, технологией изготовления резисторов. Такой «разброс» нельзя описать детерминированными функциями. В подобных случаях для описания сигналов применяют такие характеристики, которые используют для описания случайных величин (см. §3-2) - законы распределения, математическое ожидание и среднее квадратическое отклонение. Эта характеристики определяют либо опытным путем, либо на основании теоретических предпосылок о возможных изменениях измеряемой величины.
В наиболее общем виде сигналы измерительной информации могут быть представлены как случайные процессы. Например, регистрируя с помощью самопишущего прибора силу тока, потребляемого некоторым большим промышленным объектом, на диаграмме прибора получаем сложную кривую, определяемую случайным характером изменения нагрузки питающей сети. Делая повторно такие эксперименты, каждый раз будем получать новые кривые, отличающиеся друг от друга.
Семейство возможных реализаций y1(t) сигналов, подчиненное определенным вероятностным характеристикам, образует случайный сигнал Y (t) (рис. 4 - 5, а, б). Такими характеристиками могут быть закон распределения или его числовые характеристики (математическое ожидание и среднее квадратическое от-
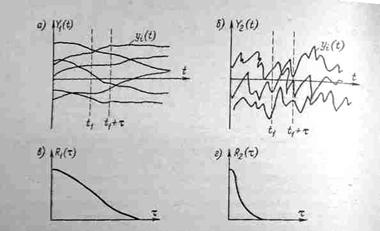
Рис. 4 -5. Реализации (а, 6) в корреляционные функции (в, г), случайных процессов Y1{t) и Y2(t)
клонение) и корреляционная функция или спектральная плотность мощности.
Случайный сигнал У (t) в некотором временном сечении t1 (рис. 4 - 5, а, б) можно рассматривать как случайную величину Y (t1), реализациями которой являются значения yi(ti). Для описания сигнала У (t) в этот момент времени применим одномерный закон распределения F (у,t1). Если этот закон не зависит от времени, т. е. F (y,t1)=F (y,t2)=F(у) при t1 ≠ t2, то такие сигналы называют стационарными (в широком смысле). Закон распределения F (у) определяет пространственную по оси ординат структуру сигнала Y (t). Иногда вместо F (у) могут быть использованы его характеристики - математическое ожидание My и среднее квадратическое отклонение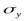 
.
Описание У(t) только законом распределения F{у) оказывается недостаточным, поскольку он не характеризует изменение сигнала во времени. Так, сигналы, приведенные на рис. 4 -5, а, б, могут иметь одинаковые законы распределения, однако обладают разной динамиков изменения во времени. Для оценки динамических свойств сигналов используют понятие корреляционной функции R (t). Для стационарных сигналов с математическим ожиданием, равным нулю, корреляционная функция определяется математическим ожиданием (пределом среднего значения) произведения значений реализаций в моменты времени t и t+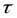 
.
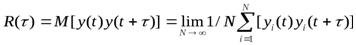(4 – 14)
где N - число реализаций случайного сигнала.
Корреляционная функция характеризует статистическую связь между мгновенными значениями случайного сигнала в различные моменты времени. Чем меньше значение корреляционной функции, тем меньше в среднем «зависит» значение сигнала У (t1 + 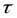) в момент времени fi+ 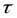от значения у (ti) в момент времени t1. На рис. 4 - 5, в, г качественно изображены корреляционные функции R1 (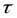) иR2(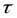), соответствующие сигналам У1 (t) и Y2 (t). Корреляционная функция R1 (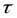) относительно слабозатухает с увеличением 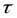, что говорит о сильной корреляцииy(ti) и у (t1+ 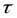) для У1 (t). На реализациях это отражается в относительно плавном изменении сигнала во времени.
Для эргодических сигналов (см. § 16-1) корреляционная функция может быть определена усреднением произведения у (t) у (t+ 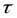) по времени для одной реализации:
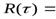
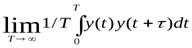(4 - 15)
При 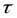=0 корреляционная функция равна дисперсии сигнала: 
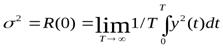. (4 - 16)
На практике часто используют понятие нормированной корреляционной функции
р(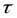)=R(
)/ 
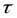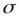2. (4 - 17)
Для характеристики частотных свойств случайных сигналов используют спектральную плотность мощности Sp (w), которая определяет распределение средней мощности сигнала по его частотам. Значения Sp(w) равны средней мощности, приходящейся на единицу полосы частот (иначе — плотности средней мощности) при различных частотах w.
Спектральная плотность мощности Sp (w) и корреляционная функция R (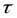) связаны соотношениями:
Sp (w) =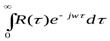 
(4-18)
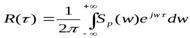(4-19)
Таким образом, для описания случайных сигналов измерительной информации применяют некоторую совокупность его ве-
Рис. 4-6. Исходная кривая у (t) сигнала и восстановленная (аппроксимирующая) кривая у* (t) полиномами Лагранжа нулевой (а) и первой (б) степени
роятностных характеристик. Так, если рассматривать сигнал как случайную величину, то его характеристикой будет закон распределения или его числовые характеристики. Если сигнал рассматривать как случайный процесс, то, кроме закона распределения, необходимо знать его корреляционную функцию или спектральную плотность мощности.
При описании случайных сигналов получили распространение нормальный и равномерный законы распределения и некоторые корреляционные функции, например,
, 
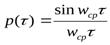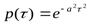, где wср, а — параметры корреляционных функций, зависящие от динамических свойств случайных сигналов.
Дискретизация сигналов. В задачах преобразования сигналов измерительной информации часто возникает необходимость представления непрерывных сигналов дискретными и восстановления сигнала по его дискретным значениям. При этом непрерывный сигнал у (t) представляется совокупностью дискретных значений у (t1), у(t2),...,y(ti) (рис. 4-6, а, б), по которым с помощью некоторого способа восстановления может быть получена оценка у* (t) исходного непрерывного сигнала у (t).
Процесс преобразования у (t) в у (t1), у (t2), …, у(ti) называется дискретизацией непрерывного сигнала. Наиболее часто применяют равномерную дискретизацию сигналов, при которой интервал времени между двумя соседними отсчетами — шаг дискретизации ∆t=ti+1-ti, остается постоянным.
Восстановление кривой сигнала по дискретным отсчетам осуществляется различными базисными функциями. В качестве таких функций широко применяют различные полиномы, в частности полиномы Лагранжа. Так, на рис. 4-6, о, б показаны исходный сигнал у (t) и восстановленный по дискретным отсчетамсигнал у* (t), полученный на основании применения полиномa Лагранжа нулевой и первой степени. Такое восстановление сигналов называют также нулевой экстраполяцией и линейной интерполяцией.
Качество приближения у (t) и y*(t) определяется погрешностью е (t) =y*(t)-y(t)- Однако использование погрешности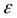 
(t) для оценки приближения у (t) и у* (t) на практике оказывается неудобным вследствие сложной временной зависимости 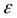(t ). Поэтому применяют некоторые числовые показатели приближения, характеризующие степень близости у (t) и y*(t). В качестве таких показателей могут быть использованы: показатель равномерного приближения
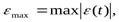
показатель среднего квадратического приближения
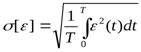, t 
[0,T]
Где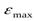 
- максимальное значение модуля погрешности восстановления на интервале представления сигнала 0 - T; 
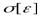-средняя квадратическая погрешность восстановления; при расчетах часто определяют 
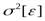- среднее значение квадрата, илидисперсию, погрешности восстановления сигнала.
Определим 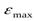и 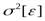при восстановлении кривой сигналаполиномами Лагранжа нулевой (n = 0) и первой (n=1) степени. На каждом интервале дискретизации (ti,ti+1),ti+1=ti+∆t имеем:
для п = 0
y* (t)=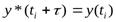 
; 
;
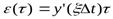для п = 1
; 
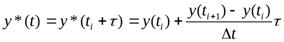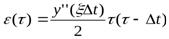
где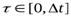 
, 
; 
; 
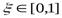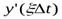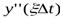- первая и вторая производные у (t) в лагранжевой точке 
, лежащей внутри интервала дискретизации. Погрешности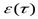 
определяются остаточным членом интерполяционной формулы Лагранжа.
А. Показатель равномерного приближения. На каждом i-м интервале дискретизации максимальная погрешность аппроксимации может быть оценена неравенствами:
для n = 0
;
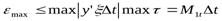для n=1
,
где M1t, M2t - максимальные значения модуля соответствующих производных на i-м интервале дискретизации. В последнем выражении max |τ (τ- ∆ t) | =∆t/4 при τ = ∆ t/2.
Для оценки максимальной погрешности восстановления по всему времени существования у (t) используется максимально возможное значение модуля соответствующей производной Мi=mах{M1t}, M2=max{M2t}, определяемое по множеству всех интервалов дискретизации. Следовательно, можно записать;
для n = 0
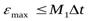; (4-20)
для n=1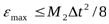 
. (4-21)
Полученные выражения позволяют также определять интервал дискретизации при заданной или допускаемой максимальной погрешности ед восстановления. Так,
для n=0
∆ t=ед/M1 (4-22)
для n=1 ∆t=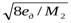 
(4-23)
Для нахождения еmax или ∆ t необходимо знать M1, или М2. Возможны различные способы определения M1 и Мг. В частности можно воспользоваться неравенством С. Н. Бернштейна, утверждающим, что если сигнал у (t) ограничен по модулю некоторым максимальным значением ут, т. е. \у (t) | ≤ym, и имеет ограниченный частотный диапазон 0 — wmax, то максимальное значение производной n-го порядка ограничено неравенством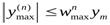 
следовательно, M1≤ w maxym; M2≤ w 2ym.
Б. Показатель среднего квадратического приближения. Среднее значение квадрата погрешности для i-го иитервала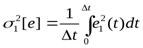 
. Для оценки приближения y*(t) по всей реализации у (t) находят усредненное по всем N интервалам дискретизации значение квадрата погрешности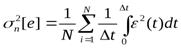 
при N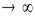 
математическое ожидание згой погрешности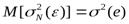 
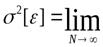
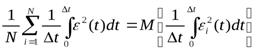(4-24)
Опуская математические выкладки, для стационарного эргодического случайного сигнала можно записать:
для n = 0
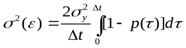; (4-25)
для n= 1
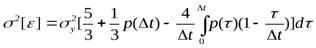
где р (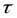) - нормированная корреляционная функция сигнала,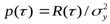 
- дисперсия сигнала у (t).
Таким образом, процедура дискретизации и восстановления -сигнала на базе полиномов Лагранжа сопровождается появлением, погрешности, зависящей, ох степени полинома, характеристик сигнала [M1; M2; p (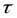)] и интервала дискретизации ∆t. В общем случае эта погрешность зависит также от вида функция, используемой при восстановлении кривой сигнала.