Работу сдать на проверку в день проведения до 20.00 часов.
Пишем разборчиво, фотографируйте сразу целый разворот.
ЗАДАНИЕ:
1. Начинаем с новой страницы тетради.
2. На полях ставим дату и тему занятия.
3. Оформляем практическую работу по образцу: теорию не писать, разбираем устно решение примеров 1, 2, 3, 4 (в тетрадь не пишем), на основе предложенных примеров аналогично решаем самостоятельно № 1, 2, 3, 4.
КРИТЕРИИ ОЦЕНКИ:
«3» - работа сдана в установленные сроки и решены любые два номера без ошибок (!!! кому трудно, можно переписать в тетрадь примеры 1, 2, 3, 4 и не решать ни один номер)
«4» - работа сдана в установленные сроки и решены любые три номера без ошибок.
«5» - работа сдана в установленные сроки и решены все четыре номера.
(!) – пример 1 и его аналог №1 самые сложные и объёмные в решении, поэтому советую оставить №1 на последнюю очередь, либо совсем не решать.
Практическая работа «Сложение и умножение вероятностей»
Теорема сложения вероятностей несовместных событий: вероятность появления одного из нескольких попарно несовместных событий, безразлично какого, равна сумме вероятностей этих событий: 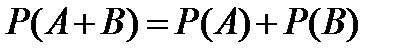
Теорема сложения вероятностей совместных событий: вероятность появления хотя бы одного из двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного появления: 
Пример1. В ящике в случайном порядке разложены 20 деталей, причем 5 из них стандартные. Рабочий берёт наудачу 3 детали. Найти вероятность того, что по крайней мере одна из взятых деталей окажется стандартной (событие А).
Решение: Если берём 3 детали наудачу, то возможны варианты:
Событие В – 1 деталь стандартная, 2 – нестандартные;
Событие С – 2 детали стандартные, 1 – нестандартная;
Событие Д – 3 детали стандартные.
Значит, событие А=В+С+Д и его вероятность 
Имеем по задаче: 20 деталей – всего, 5 деталей – стандартные, 15 деталей – нестандартные.
1) Число n всех равновозможных независимых исходов = числу сочетаний из 20 по 3, т.е.
 (после сокращений)
(после сокращений)
m – число исходов, которые благоприятствуют событию А.
2) Событие В – 1 деталь стандартная, 2 – нестандартные.
- число способов 1 станд. из 5 имеющихся станд. = числу сочетаний из 5-ти по 1:

- число способов выборки 2 нестанд. из 15 нестанд.:

- получаем, что 
- находим 
3) Событие С – 2 детали стандартные, 1 – нестандартная.
- число способов 2 станд. из 5 имеющихся станд. = числу сочетаний из 5-ти по 2:

- число способов выборки 1 нестанд. из 15 нестанд.:

- получаем, что 
- находим 
4) Событие Д – 3 детали стандартные.
- число способов 3 станд. из 5 имеющихся станд. = числу сочетаний из 5-ти по 3:

- число способов выборки нестанд. нет
- получаем, что 
- находим 
Итак, 
Ответ: 0,602
№ 1. В ящике в случайном порядке положены 10 деталей, из которых 4 стандартных. Контролёр взял наудачу 3 детали. Найдите вероятность того, что хоты бы одна из взятых деталей оказалась стандартной. (Ответ: 0,833)
Пример 2. Найти вероятность того, что наудачу взятое двузначное число окажется кратным либо 3, либо 5, либо тому и другому одновременно.
Решение: Пусть
А – событие, что число кратно 3;
В – событие, что число кратно 5.
События А и В совместные, тогда 
Всего 90 двузначных чисел: 10, 11, 12, …, 98, 99.
Из них 30 кратны 3, т.е. 
Из них 18 кратны 5, т.е. 
Из них 6 кратны 3 и 5 одновременно, т.е. 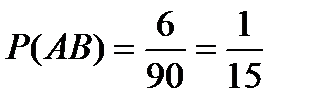
Находим, 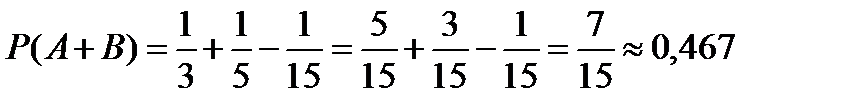
Ответ: 0,467
№ 2. Найти вероятность того, что наудачу взятое двузначное число окажется кратным либо 4, либо 5, либо тому и другому одновременно. (Ответ: 0,4)
Теорема умножения вероятностей независимых событий: вероятность совместного появления двух независимых событий равна произведению вероятностей этих событий: 
Теорема умножения вероятностей зависимых событий: вероятность совместного появления двух зависимых событий равна произведению одного из них на условную вероятность второго: 
Пример 3. В одной урне находятся 4 белых и 8 черных шаров, в другой – 3 белых и 9 черных. Из каждой урны вынули по шару. Найти вероятность того, что оба шара окажутся белыми.
Решение: Пусть
А – появление белого шара из первой урны (их всего 4);
В – появление белого шара из второй урны (их всего 3).
А и В независимые события.
Всего шаров и в первой, и во второй урне по 12.
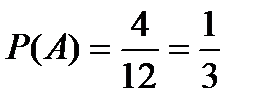 ;
; 
По формуле 
Ответ: 0,083
№ 3. В одной коробке находятся 6 синих и 8 желтых карандашей, в другой – 2 синих и 10 желтых. Из каждой коробки вынули по карандашу. Найти вероятность того, что оба карандаша окажутся желтыми. (Ответ: 0,476)
Пример 4. В ящике находится 12 деталей, из которых 8 стандартных. Рабочий берёт наудачу одну за другой две детали. Найдите вероятность того, что обе детали окажутся стандартными.
Решение: Пусть
А – первая взятая деталь стандартная;
В – вторая взятая деталь стандартная.
Вероятность того, что первая взятая деталь стандартная: 
Вероятность того, что вторая взятая деталь стандартная (с учётом, что первая стандартная, теперь всего деталей 11 и из них 7 стандартных): 
По формуле 
Ответ: 0,424
№ 4. В урне находятся 6 шаров, из которых 3 белых. Наудачу вынуты один за другим два шара. Найдите вероятность того, что оба шара окажутся белыми. (Ответ: 0,2)