Список вопросов для подготовки к экзамену по дисциплине
- Метод координат.
- Длина отрезка.
- Деление отрезка в заданном соотношении.
- Полярные координаты.
- Связь между полярными и прямоугольными координатами.
- Векторы и действия над ними.
- Линейные операции над векторами. Умножение вектора на число. Сложение векторов.
- Свойства линейных операций.
- Алгебраическое описание вектора.
- Умножение вектора на число.
- Сложение векторов.
- Скалярное произведение векторов.
- Свойства скалярного произведения.
- Условия коллинеарности и ортогональности векторов.
- Направляющие косинусы.
Алгебраическая проекция вектора на вектор.n-мерное векторное пространство.- Уравнение прямой в
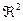(на плоскости). - Уравнение прямой с угловым коэффициентом в 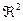(на плоскости).
- Уравнение прямой, проходящей через заданную точку в 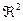(на плоскости) с известным направляющим вектором
- Уравнение прямой, проходящей через заданную точку в 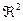(на плоскости).
- Уравнение прямой, проходящей через две заданных точки в 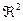(на плоскости).
- Угол между двумя прямыми в 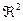(на плоскости).
- Уравнение прямой, проходящей через данную точку перпендикулярно (или параллельно) к данной прямой в 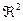(на плоскости).
- Уравнение прямой в отрезках в 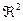(на плоскости).
- Расстояние от точки до прямой в 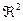(на плоскости).
- Кривые второго порядка. Уравнение окружности.
- Кривые второго порядка. Уравнение эллипса.
- Кривые второго порядка. Уравнение гиперболы.
- Кривые второго порядка. Уравнение параболы.
- Плоскость в
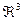(трехмерном пространстве). - Уравнение плоскости в отрезках.
- Угол между плоскостями.
- Расстояние от точки до плоскости.
- Общее уравнение прямой в 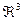(трехмерном пространстве).
- Параметрические уравнения прямой в 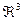(трехмерном пространстве).
- Канонические уравнения прямой в 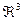(трехмерном пространстве).
- Уравнение прямой, проходящей через две заданные точки в 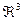(трехмерном пространстве).
- Угол между двумя прямыми в 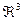(трехмерном пространстве).
- Условия параллельности и перпендикулярности прямых в 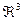(трехмерном пространстве).
- Угол между прямой и плоскостью.
- Взаимное расположение прямых и плоскостей (условия параллельности и перпендикулярности) в 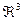(трехмерном пространстве).
- Матрицы. Основные определения.
- Действия над матрицами. Транспонирование, сложение, умножение на число, произведение матриц.
- Теория определителей. Основные понятия.
- Свойства определителей.
- Обратная матрица.
- Ранг матрицы.
- Базисный минор. Теорема о базисном миноре.
- Элементарные преобразования над матрицами.
- Системы линейных алгебраических уравнений. Основные понятия.
- Матричный способ решения систем линейных алгебраических уравнений.
- Теорема Крамера.
- Исследование систем линейных алгебраических уравнений. Теорема Кронекера-Капелли.
- Равносильные системы линейных алгебраических уравнений. Элементарные преобразования над строками матрицы СЛАУ.
- Однородные системы линейных алгебраических уравнений.
- Решение системы линейных алгебраических уравнений методом исключения.
- Метод Гаусса решения системы линейных алгебраических уравнений (метод полного выделения базисных переменных).
- Линейная зависимость векторов.
- Ранг и базис системы векторов n-мерного пространства.
- Базис n-мерного пространства.
- Разложение произвольного вектора по векторам базиса.
- Собственные числа и собственные вектора матрицы. Основные понятия.
- Отыскание собственных чисел матрицы.
- Теорема Гамильнона-Кэлли.
- Отыскание собственных векторов матрицы.
- Свойства собственных чисел матрицы.
- Свойства собственных векторов матрицы.
- Линейная балансовая модель.
- Продуктивная модель Леонтьева. Математический критерий продуктивности. Связь продуктивности матрицы с ее собственными числами.
- Задача определения плана производства.
|
|
|
|
Элементы математического программирования.
1. Примеры экономических задач, решаемых методами математического программирования.
2. Классификация основных методов математического программирования.
3. Симплекс метод.
3.1. Симплексные таблицы.
3.2. Экономическая интерпретация элементов симплексной таблицы.
3.3. Улучшение опорного решения.
3.4. Определение ведущих столбца и строки.
3.5. Выбор начального допустимого базисного решения.
3.6. Введение искусственных переменных.
4. Понятие о теории двойственности.
5. Транспортные задачи.
5.1. Экономическая и математическая формулировки транспортной задачи.
5.2. Метод потенциалов.
5.3. Основные способы построения начального опорного решения.
5.4. Транспортные задачи с нарушенным балансом производства и потребления.