ТОПОГРАФИЧЕСКИЕ СЪЕМКИ В МАСШТАБЕ 1 : 5000 И 1 : 2000

ТАХЕОМЕТРИЧЕСКАЯ СЪЕМКА

121.- Даны отсчеты по вертикальному кругу теодолита (Т5). Вычислит^ углы наклона линий (табл. 42).

122. Расстояние D измерено нитяным дальномером. Вычислить поправку за отклонение коэффициента дальномера от 100 (табл. 43).

Величина I равна разности между отсчетами по нижней и верхней нитям. Из полученных для каждого расстояния значений вычисляют среднее.

По полученным значениям Р составляют таблицу поправок из двух столбцов. В правом столбце выписывают значения Р через 0,1 м, в левом — расстояния, которым соответствуют значения Р. ч/123. Вычислить горизонтальные проложения линий d, длины которых измерены нитяным дальномером с коэффициентом, не рав­ным 100. При решении следует пользоваться таблицей поправок Р, составленной при решении предыдущей задачи. В табл. 44 даны следующие величины:

Таблица 44

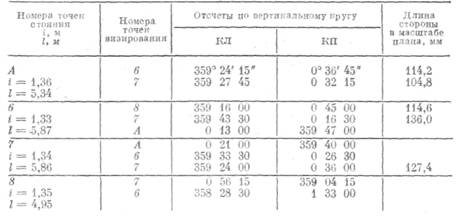
124. Длины сторон хода, проложенного для обоснования тахео­метрической съемки, измерены дифференциальным дальномеров ДД-3. Даны отсчеты по рейкам и вертикальному кругу теодолита (табл. 45). Цена деления основных шкал реек равна 2 см. Коэффи­циент дальномера К = 100,00, МО = 359° 59'.

Пояснение.

а. Отсчет по рейке (например, с точки 1 на п. Бор) складывается
из трех частей: отсчет по основной шкале рейки — 61; номер совме­
щенного штриха верньера — 0,7; число делений верньера от его
лульпункта до средней горизонтальной нити сетки нитей — 0,071;

б. Отсчет I но рейке вычисляется как средний из отсчетов по
белой (4) и желтой (1_Ж) сторонам рейки. Поскольку цена деления
основной шкалы рейки 2 см, отсчеты по рейке необходимо удвоить;
взамен этого (для контроля и уменьшения ошибки отсчета) произ­
водят по два отсчета по каждой стороне рейки V и I", а затем их
складывают. Расхождение между ними не должно превышать
1: 2000 отсчета. В примере полученные по белой стороне рейки
отсчеты расходятся на 61,771 — 61,747 = 0,024 см.

К отсчетам по желтой стороне добавлена величина 11,111 см — на столько нуль верньера желтой стороны сдвинут относительно нуля белой стороны рейки. Расхождение между отсчетами 1_б и 1_Ж не должно превышать 1: 3000 отсчета 1_б или /_ж:

если допуск выдержан, вычисляют окончательное значение. В примере

в. Дальномерное расстояние D = 100/ + с = 123,54 + 0,01 =
= 123,55 м (с — постоянное слагаемое).

г. По D и углу наклона биссектрисы параллактического угла
v +.17' = —3° 16' + 17' = -2° 59' из таблиц Г. Г. Егорова
или других авторов выбирают поправку за наклон — 0,37 м (v —
угол наклона визирной оси, наведенной на совмещенный штрих
верньера). Наконец, находят горизонтальное проложение d =
= 123,55-0,37 = 123,18 м.

125. С какой точностью нужно получить отсчет I по дальномерной
нити при различных расстояниях, чтобы обеспечить относительную
ошибку дальномерного расстояния 1: 300? Сделать анализ для рас­
стояний 50, 100, 150, 200 и 250 м,_; используя формулу

П р.и м е ч а н и е. Следует учесть, что длина отрезка I рейки равна разности отсчетов по дальномерным нитям.

126. Подсчитать величину ожидаемой ошибки определения рас­
стояния нитяным дальномером из-за наклона е рейки в створе изме­
ряемой линии. Принять при этом расстояние до рейки D — 150 м,
угол наклона линии визирования 1) v = 8°; 2) v = 12°, угол наклона
рейки в створе s = 3°. Какой вывод вытекает из полученных ответов?

"Указание. Следует воспользоваться формулой

127. Установить при помощи таблиц величину ожидаемой ошибки превышения по условиям предыдущей задачи и при наличии ошибок, определения расстояния, полученных в результате ее решения. Какие меры следует принять, чтобы обеспечить в таких случаях необходимую точность и сходимость значений превышения, измерен­ного в прямом и обратном направлениях в пределах допуска ин­струкции?

128. В проложенном разомкнутом тахеометрическом ходе сумма измеренных левых углов 2 Р_Лев = 979° 11,0'; дирекционные углы начальной и конечной исходных линий соответственно равны а_тч = — 147° 14,8' и к_кон == 226° 27,4', число углов п — 5. Вычислить угловую невязку и определить, допустима ли она.

129. Решить предыдущую задачу при условии 2 р_прав = 973° 24,1'; а_кйч = 189° 56,6'; а_коя = 296° 34,3'; п = 6.

130. Сумма внутренних углов в пятиугольном полигоне 2 (3 = = 539° 58,7'. Допустима ли угловая невязка, если число углов п = 5?

131. Сумма приращений координат в тахеометрическом ходе
2Ах = +205,24 м и ZAy = —412,30 м; координаты начального
и конечного пунктов равны ж_нач = 5 812 739,62 м, у_нш =
= 7 653 211,83; х_ков = 5 812 944,75 м, у_&оп = 7 652 799,26 м.
Длина хода s = 480,5 м, число линий в ходе п = 3. Определить,
допустимы ли невязки в сумме приращений координат (fs_AQ„ =
= s (м)/400 У~п, где п — число линий в ходе).

132. Вычислить абсолютную высоту точки 2 по результатам три­гонометрического нивелирования, если даны: высота точки 1 H_v дальномерное расстояние D между точками, угол наклона визирной, линии v, высота инструмента г и высота визирной цели — рейки I (табл. 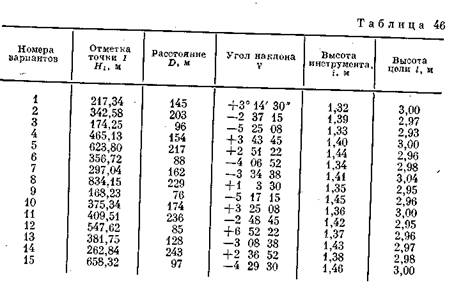46).

133. По условиям предыдущей задачи найти отметку точки 2, считая, что расстояние между точками является горизонтальным проложением d линии 1 — 2.

134. В табл. 47 даны прямые и обратные превышения между точ­ками тахеометрического хода. Определить, допустимо ли расхожде­ние между ними, и вычислить средние значения превышений,

Таблица 47

135. Уравнять превышения между точками тахеометрического
хода (табл. 48), предварительно убедившись в допустимости высот­
ной невязки хода, и вычислить отметки точек 1 и 2 хода.

Таблица 48

136. На станции тахеометрического хода произведена тахео­
метрическая съемка. В табл. 49 дана выписка из пикетного журнала
результатов измерений, выполненных теодолитом ТЗО, при положе­
нии «круг право».

Переписать эти данные в пикетный журнал, вычислить отметки реечных точек и в соответствии с прилагаемым абрисом (см. рис. 31) составить план местности в масштабе 1: 2000 с сечением рельефа через 1 м. Ориентирование плана произвести по заданному дирек-ционному углу стороны хода.

Пояснение. При обработке пикетного журнала находят значения угла наклона v = КП — МО; вычисляют превышения пикетных точек над точкой стояния инструмента, причем величина ¹ _ZD sin 2v = %' выбирается из тахеометрических таблиц.

 

МЕНЗУЛЬНАЯ СЪЕМКА

137. Для определения коэффициента К кривой превышения
у кипрегеля-автомата КА-2 между двумя точками местности, уда­
ленными друг от друга на 100 м, дважды измерено превышение —
проложением хода геометрического нивелирования h_HllB и много-

- кратно при помощи исследуемой кривой превышения /г_кр. Получены: Ант — 8,523 м и среднее значение h_liP = 8,55 м. Вычислить коэф­фициент К кривой. (К — K_Hh_msh_KP)

При каких расхождениях (для кривых К₁₀, К₂₀, К₁₀₀) факти­ческого коэффициента кривой от номинального его значения можно пользоваться последним.

138. По полученному в предыдущей задаче коэффициенту К кривой найти поправочный коэффициент N и вычислить исправлен­ное превышение. Измеренное при помощи кривой значение превыше­ния К = +4,86 м. (JV₁₀ = 0,1#₁₀; N₂₀ = 0,05 К_г0; N_m = 0M K_1W)

139. Полученные показания рабочей буссоли А и буссоли пар­тии В равны:

Поправка буссоли партии и₂ = +0,2°. Определить поправку рабо­чей буссоли, (v = v_x-x- v₂; v_x = Л_ср — В_сР)

140. Стандартная номенклатура топографического плана L-37-4 (131-в). Определить масштаб плана и размеры рамки лист а.

141. Номенклатура трапешш М-38-84 (112-а). Найти географи­ческие координаты и по ним — прямоугольные координаты Га­усса — Крюгера вершин углов рамок трапеции, пользуясь табли­цами прямоугольных координат углов рамок трапеций топографи­ческих съемок масштаба 1: 5000.

Как наносятся углы рамки трапеции и какой при этом контроль?

142. На планшете в масштабе 1: 5000 нанесены два пункта А и В
геодезической сети по их координатам:

Определить, правильно ли нанесены указанные пункты, если расстояние между ними на планшете I получилось равным 265,8 мм.

143. На трапеции, координаты углов рамки которой даны
в табл. 50, нанесена линия 1 — 2.

Таблица 50

Координаты точек 1 и 2:

х_г = 5 362 850,0 м, у_х = +109 700,0 м, х₂ = 5 362 600,0 м, ^₂=+109 800,0 м.

Длина линии 1 — 2 слишком короткая для ориентирования по ней планшета.

Для получения на планшете ориентирной линии достаточной длины вычислить координаты точек а_х и а₂, лежащих на продол­жении линии 1 — 2, соответственно в противоположные от нее напра­вления и близко к крлям трапеций.

Пример решения для получения точки. а₁.

а. Составляют схематический в уменьшенном виде чертеж коор­
динатной сетки. Для этого вычерчивают сетку квадратов (условную
километровую сетку), подписывают выходы километровых линий.
Крайнюю нижнюю линию принимают равной 5361,0 км, крайнюю
левую линию — 108,5 км. Оцифровывают все остальные линии,
учитывая, что абсциссы возрастают снизу вверх, а ординаты —
слева направо; сторону квадрата, равную в натуре 1 дм, согласно
масштабу плана (в данном случае 1: 5000) принимают за 500 м.

По координатам приближенно наносят вершины углов рамок трапеции и, соединив их, получают рамки трапеции. Затем по коор­динатам приближенно наносят точки 1 и 2 и, соединив их, получают линию 1 — 2.

б. Продолжив линию 1 — 2 до северной рамки, находят, примерно
во сколько раз расстояние от точки 1 до рамки больше длины ли­
нии 1 — 2. Это будет коэффициент К. В примере можно принять его
равным 2.

в. Вычисляют приращения координат между точками 1ик:

Ах = х₁ — х₂ = 250,0 м, Ау = у_г — у₂ ==— 100,0 м.

г. Находят приращения координат между точками а_х и 1:

Ах' = КАх = 2х 250,0 м = + 500 м, Ау' = КАу = 2х (—100,0) м = -200 м.

д. Вычисляют координаты точки а_х:

х_а1 = х_х + Ах' = 5 363 350,0 м, г/а, = Ух + Ау' = +109 500,0 м.

е. По координатам наносят точку а_г. Она должна находиться
на продолжении линии 2 — 1. Аналогично находят точку а₂.

144. Кроме двух геодезических точек 1 и 2, за пределами трапеции
М-38-129-(224), рассмотренной в предыдущей задаче, находится
геодезический пункт Бор, не помещающийся на планшете. Его
координаты

х = 5 361 200,0 м,

у = + 107 100,0 м.

Учитывая условия предыдущей задачи, вычислить координаты точки С, расположенной вблизи западной рамки трапеции, для получения ориентирной линии 1 —с, совпадающей с направле­нием 1 — Бор.

145. На точке местности при ориентированном планшете ориен­
тир-буссоль была приложена к стороне рамки трапеции. Средний
отсчет по северному концу магнитной стрелки оказался равным
+6,5°. Поправка буссоли равна —0,3°. Вычислить значение скло­
нения магнитной стрелки.

146. На топографическом; плане принята прямоугольная раз­
графка. На точке при ориентированном планшете ориентир-буссоль
была приложена к вертикальной линии сетки координат. Средний
отсчет по магнитной стрелке А = +5,6°, поправка буссоли равна
v = +0,2°; сближение меридианов у = +0°18. Вычислить склоне­
ние магнитной стрелки.

147. Вычислить допустимую величину ошибки центрирования
мензулы при съемке в масштабах 1: 2000 и 1: 5000 и сравнить
полученные ответы с допусками инструкции.

148. Даны результаты измерений на пунктах геометрической
сети, образующих на местности два примыкающих друг к другу
треугольника (табл. 51) А 6 7 ж 87 6. Вычислить средние превыше­
ния между пунктами, высотные невязки в треугольниках и после
увязки превышений методом сравнения невязок определить отметки
точек 6, 7, 8. Масштаб съемки 1: 5000. Отметка исходного пункта А
равна Н_А = 543,68 м.

Таблица 51

Примечание, а. По измеренным на планшете длинам сто­рон геометрической сети расстояние между точками вычисляют с точностью до 0,5 м.

б. Допустимые невязки в превышениях в каждом треугольнике не должны превышать (в метрах) величин 0,2 "J/L, где L — длина периметра треугольника в километрах.

149. С определяемой точки D углы между направлениями на пункты А и В и на пункты В ж С соответственно равны 55° и 60°.

Координаты пунктов А, В и С указаны в табл. 52.

Определить в произвольном масштабе положение точки отно­сительно пунктов А, В и С спосо­бом Болотова.

150. Точка D получена на план­шете решением задачи Потенота. По измеренным с нее углам на­клона и расстояниям до исходных пунктов А, В и С вычислены превышения между определяемой точкой и исходными пунктами, даны отметки этих пунктов:

Я_д = 182,56 м; Н_в = 212,34; Я_с = 196,73;

h_DA=— 24,02 м; h_DB = +5,71 м; h_DC= —10,06 м.

Вычислить высоту точки.

151. Линейная невязка мензульного хода равна 0,6 мм в мас­штабе плана. Длина хода равна 856 м. Определить, допустима ли относительная невязка хода, если масштаб съемки 1: 5000.

152. В мензульном ходе, состоящем из четырех линий, сумма измеренных превышений 2 h == —10,25 м. Длина хода равна 784*м. Отметки исходных начального и конечного пунктов Н_тч'= 456,78 м, Я_к0„ = 446,39 м.

Допустима ли высотная невязка хода?

КОМБИНИРОВАННАЯ СЪЕМКА НА ФОТОПЛАНЕ

153. При проложении основного высотного хода тригонометри­
ческим нивелированием на станции 1 дважды определено превышение
на две высоты рейки. Найти значения превышения, установить,
допустимо ли расхождение между ними, и вычислить отметку наблю­
даемой точки хода 2.

Результаты измерения приводятся в табл. 53. Отметка точки 1 Н_х = 879,65 м.

Указание. Выписать из табл. 53 заданные величины в жур­нал топографической съемки и там выполнить вычисления при по­мощи таблиц превышений для дальномерных расстояний (Г. Г. Его­рова или других авторов).

154. Отметка точки связи на стыке двух планшетов получена
дважды: Н'_с = 545,26, Н"_с = 545,67 м.

Таблица 53

Допустимо ли расхождение между указанными значениями, если высота сечения рельефа равна 1м?

155. Предельные допустимые ошибки высот точек съемочного
высотного хода не должны превышать ^х/₆ принятой высоты сечения
рельефа. Какую невязку хода можно допустить при высоте сечения
рельефа 1 м?

156. При проложении основного высотного хода сумма превыше­
ний 2й = 16,73 м, отметки начальной и конечной точек хода соот-

, ветственно равны Н_нйЧ = 238,54 м и Н_кт = 222,20 м. Допустима ли невязка хода при высоте сечения рельефа 2 м?

157. Отметка точки стояния мензулы Н_ст = 342,51 м. Дально-
мерное расстояние D = 183 м. Средняя нить наводилась на точку
рейки, соответствующую высоте инструмента. Отсчет по вертикаль­
ному кругу КЛ = 354° 38', МО = 359° 59'. Вычислить отче™7
пикета.

158. Отметка станции Я_ст = 285,24 м, высота инструмента i =
= 1,42 м. На какую высоту /рейки следует наводить среднюю нить,
чтобы значение Н₀ = Н_ст + i — I выражалось целым числом метров?

159. При наборе пикетов Я₀ = Я_ст + i — I = 312 м. Отсчет
по вертикальному кругу КЛ = 2° 45', МО = 0° 30',_; расстояние
D == 192 м. Вычислить отметку пикета.

160. При съемке на фотоплане в масштабе 1: 5000 отметка выра­
женной контурной точки определена путем наведения средней нити
на землю у основания контурной точки. В табл. 54 даны: измеренная
на плане длина отрезка от точки стояния мензулы до опознанной
пикетной точки d, отсчет КЛ, значение МО, высота инструмента i,
отметка станции Н_ст. Вычислить отметку пикета.

5 Заказ 121 65

Таблица 54

Пояснение. Величину h₀ выбирать из таблиц превышений для горизонтальных проложений.

161. Съемка рельефа произведена горизонтальным лучом. В табл. 55 даны отметка точки стояния инструмента #,-, высота инструмента i и отсчеты а по рейке, установленной последовательно на четырех пикетах. Вычислить их отметки.

Таблица 55

162. С точки, расположенной на расстоянии d = 45 м от фермы высоковольтной электролинии,, измерены углы наклона на верх фермы и на ближайшую к инструменту точку ее основания. Получены v_B = +29° 35' и v₀ = +0° 19'. Вычислить высоту фермы.

163. Выбрана точка, удаленная от дерева на 21,5 м, с которой вершина дерева наблюдается под углом 45° с высоты 1,5 м. Опре­делить высоту дерева.

164. Измеренная на высоте груди длина окружности ствола дерева равна 0,70 м. Чему равен диаметр ствола?

165. На лесном участке с однородной густотой деревьев измерены две взаимно перпендикулярные линии и подсчитано число стволов, расположенных в непосредственной к ним близости. Вдоль первой линии длиной 65 м оказалось 10 стволов, вдоль второй линии длиной 60 м — 8 стволов. Вычислить среднее расстояние между деревьями.

166. На прямолинейном участке реки установлены две вехи на расстоянии 100 м друг от друга. Пущенный по течению поплавок проплыл расстояние между вехами за 8 мин и 20 с. Чему равняется поверхностная скорость течения реки?

167. Опишите, как отличить на местности:

а) телефонную линию от электролинии;

б) электролинию низкого напряжения от высоковольтной;

в) шоссе от усовершенствованного шоссе или от автострады;

г) балку от оврага;

д) проходимое болото от непроходимого;

е) огнеупорный дом от неогнеупорного;

ж) приусадебный участок от земли общего пользования.

Глава VIII ТЕОРИЯ ОШИБОК ИЗМЕРЕНИЙ

РАВНОТОЧНЫЕ ИЗМЕРЕНИЯ

168. Угол, истинное значение которого X = 56° 17' 24,4", изме­
рен 12 приемами. При этом получены следующие значения секунд:

,5; 23,8; 22,6; 22,2; 23,9; 25,5; 24,7; 22,6; 20,4; 26,3; 21,3; 24,1. Подсчитанная предельная ошибка измерения 5". Вычислить истин­ные ошибки и проверить, отвечают ли они свойствам случайных ошибок.

169. Ответьте на следующие вопросы:

а. Угол измерен высокоточным теодолитом с ошибкой 1', рассто­
яние измерено лентой с ошибкой, равной 5 м; превышение определено
геометрическим нивелированием с ошибкой 0,5 м. Можно ли считать
эти ошибки грубыми?

б. Ряд измерений выполнен со следующими ошибками: +1; —1;
—3; 0; —4; —1; +2; —2; —3. Являются ли эти ошибки случайными
или носят систематический характер?

170. К какой категории следует отнести ошибки: коллимацион­
ную, за неравенство подставок, за эксцентриситет алидады, делений
лимба, наведения, отсчитывания, за рефракцию? Ответы обоснуйте.

5* 67

171. Расстояние измерено лентой и нитяным дальномером;, длина стороны треугольника измерена лентой и получена из ренщния треугольника; высота визирного цилиндра над центром пункта измерена рулеткой и получена аналитически* один из углов тре­угольника измерен теодолитом и получен по остальным двум' углам. В каждом случае одно измерение непосредственное. Какие измерения являются здесь косвенными?

172. Линия, истинное значение длины которой равно 125,43 м, измерена 6 раз. Результаты измерений следующие: 125,56; 125,49; 125,39; 125,38; 125,44; 125,35 м. Определить среднюю, вероятную и среднюю квадратическую ошибки одного измерения.

Решение (табд. 56).

Таблица 56

173. Один и тот же угол, истинное значение которого X =
= 75° 43' 26", получен из двух рядов измерений (табл. 57).

Таблица 57

I ряд измерений.--"■•-...

75° 53'27,0"; 26,2"; 28,3"; 20,0"; 24,9"; 24,1"; 27,4"; 28,9"; 26,0"

II ряд измерений

75° 43'27,9"; 23,1"; 28,4"; 29,0"; 23,9"; 25,3"; 28,2"; 27,1"; 25,0"

Определить среднюю, вероятную и среднюю квадратическую ошибки по каждому ряду измерений. Указать, какой вывод можно сделать из сравнения определяемых ошибок. Какие из них лучше отражают точность измерений?

174. Истинные ошибки результатов пробных определений пре­
вышений равны в миллиметрах: +0,11; +0,05; —0,02; +0,25; +0,04;
—0,20; —0,12; —0₃07; +0,50; —0,03; +0,13. Найти среднюю квадра­
тическую, среднюю и вероятную ошибки одного измерения. Про­
верить, имеются ли среди истинных ошибок грубые ошибки.

175. Средние квадратические ошибки равны: 1) измерения угла т = 20"; 2) отсчета по рейке т₀ = 0,7 мм; 3) взаимного положения точек m_s = 0,3 м. Вычислить значения соответствующих предель­ных ошибок.

176^ Определить среднюю квадратическую ошибку суммы углов одного треугольника, если угловые невязки треугольников в триан­гуляционной сети равны +1,1"; —2,0"; +1,5"; — 3,1"; —0,9"; +3,0"; +1,2"; -0,3".

Пояснение. Угловые невязки треугольников рассматри­ваются как истинные ошибки сумм углов.

177. Определить, какая из указанных двух линий измерена
точнее, если известны их длины и соответствующие средние квадра­
тические ошибки измерения:

di = 145,20 м, т_х = 0,14 м; tf₈ = 483,05 м, т_% = 0,24 м. -

178. Вычислить относительную^ошибку измерения линии, длина которой оказалась равной d — 125,31 м; средняя квадратическая ошибка измерения т = 7,2 см.

179. Определить, с какой относительной ошибкой проложен теодолитный ход, если абсолютная (линейная) ошибка Д,_бс = 1,43 м, а длина хода L = 2145 м.

180. Светодальномер обеспечивает измерение расстояний со сред­ней квадратнческой ошибкой т = 3 см. Какую можно ожидать относпте.тьнтю ошибку при измерении сторон длиной: 1) 200 м:

500 м; 3) 1000 м; 4) 1200 м.

181. Угол измерен шестью приемами. Получены значения угла:
1) 35° 12' 56"; 2) 35° 12' 55"; 3) 35° 12' 59"; 4) 35° 13' 02";

35° 13' 00"; 6) 35° 12' 59". Вычислить вероятнейшее значение угла.

Проверить правильность вычислений, используя свойство вероят-

нейших ошибок.

Решение (табл. 58).

Таблица 58

а\— приближенное значение (обычно выбирается наименьшее) из­меренной величины.

182. При определении расстояния насадкой ДНТ параллакти­
ческий угол измерен шестью приемами. В табл. 59 даны результаты
измерений (в делениях).

Таблица 59

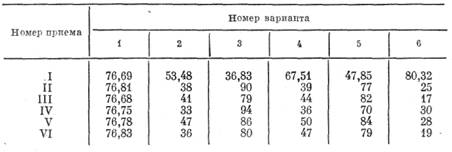
Вычислить вероятнейшее значение измеренного угла. Проверить правильность вычисления, используя свойство вероятнейших ошибок.

183. Определить среднюю квадратическую ошибку расстояния D,
измеренного нитяным дальномером, если коэффициент дальномера
К — 100, а отсчет по рейке сделан с ошибкой т; = 1 см.

Решение. Для решения задач по оценке точности функций измеренных величин необходимо:

а) выбрать формулу, по которой вычисляется оцениваемая вели­
чина, в данном случае D = К1',

б) установить общий вид функции, в данном случае у — кх;

в) зная формулу средней квадратической ошибки этой функции,
подставить в нее значения заданных величин, в нашем случае т_у =
— кт_х, тогда

лги — кт₍, m_D = 100 -1 см = 100 см, m_D = 1 м.

/ 184. Превышение определено геометрическим нивелированием по способу «вперед». Определить его среднюю квадратическую ошибку, если ошибка измерения высоты инструмента т₍ = 3 мм, а ошибка отсчета по рейке (взгляда) т_ВЗГл = 2 мм.

185. На местности были измерены все три угла в треугольнике со средними квадратическими ошибками т_а = 0,28"; тр = 0,24" и ту = 0,50". Вычислить среднюю квадратическую ошибку суммы углов в данном треугольнике.

186. При обработке результатов измерений углов на станции угол 1,3 вычисляется как сумма двух измеренных углов (1,2 и 2,3). Определить его среднюю квадратическую ошибку, если каждый измеренный угол получен с ошибкой ш = 2".

187. Превышение на станции получено геометрическим нивелиро­ванием из середины как разность двух взглядов. Определить среднюю квадратическую ошибку превышения, если ошибка взгляда равна

2 мм.

188. В теодолитном ходе п углов, каждый из которых измерен
со средней квадратической ошибкой m = 30". Вычислить среднюю

квадратическую ошибку суммы углов в ходе. Чему равна предель­ная ошибка суммы углов во всем ходе, если принять предельную ошибку измерения угла А_пред = 2т?

189. Длина линии АВ измерена нитяным дальномером по ча­стям — с концов линии определены отрезки АС ж ВС. Каждый отсчет по рейке получен как разность двух отсчетов по крайним нитям, средняя квадратическая ошибка отсчета по одной нити равна т₀ — == 0,5 см. Коэффициент дальномера К = 100. Вычислить среднюю квадратическую ошибку то длины линии АВ.

190. Угол С получен как дополнение до 180° к сумме двух других измеренных углов А я В треугольника. Найти среднюю квадрати­ческую ошибку угла С, если каждый из углов А и В измерен со средней квадратической ошибкой m = 5". -

191. По условиям задачи 175 определить среднюю квадратиче­скую ошибку измерения одного угла (по невязкам треугольников).

Пояснение. В задаче 175 даны невязки треугольников w, являющиеся истинными ошибками суммы углов; средняя квадрати­ческая ошибка суммы углов треугольника

но в то же время m-z = пгУЪ, где тп — средняя квадратическая ошибка измерения одного угла, откуда m — т^1УЪ. Подставляя полученное значение m_s, получим

Эта формула известна под названием формулы Ферреро.

Далее подставляем числовые значения задачи 175 и вычисляем среднюю квадратическую ошибку измерения одного угла треуголь­ника.

192. В сети триангуляции 3 класса получены невязки треуголь­ников: +1,6"; +3,7"; -2,0"; -0,6"; +1,0"; -2,4"; +2,5"; -4,0"; +1,3"; —3,2". Определить, допустима ли средняя квадратическая ошибка измерения угла, если согласно инструкции она не должна превышать 1,5".

193. Найти среднюю квадратическую ошибку угла, вычисленного как разность двух направлений, если средняя квадратическая ошибка одного направления равна т_н = 7".

194. Решить задачу 189, предполагая, что отсчет по рейке получен как удвоенное произведение разности отсчетов по средней нити и по одной из крайних нитей. Доказать, что ошибка определения расстояния дальномером при отсчитывании по средней и крайней нитям и последующем удваивании вдвое больше, чем при отсчете по крайним нитям.

195. Средняя квадратическая ошибк! нивелирования, приходя­щаяся на 1 км хода, равна т = 5 мм. Чему равна средняя квадрати-

ческая ошибка нивелирного хода, в котором число километров равно Ы Какую предельную ошибку можно допустить в ходе, если принять предельную ошибку на 1 км равной А_Пр_ед = 2то?

196. Найти среднюю квадратическую ошибку щ определения площади прямоугольника, вычисленной по измеренным на плане сторонам а = 520 м и Ъ = 645 м. Масштаб плана 1: 10 000. Средние квадратические ошибки измерения длин сторон т_а — т_ь = 0₃2 мм.

Решение. Р = аЪ;

~-V(-£):-.+(£):-ii

считая вначале Ъ, а затем а постоянными, находим частные произ­водные функции Р по аргументам а и Ъ:

дР, дР
—— = Ь; —— = а.
да до

Подставив полученные значения частных производных в формулу средней квадрати-ческой ошибки функции и учитывая, что

^та = ^тЬ — ™% ПОЛУЧИМ

197. Найти среднюю квадратическую ошибку определения площади фигуры ABCDE (рис. 32), вычисленной по измеренным на плане линиям: а = 422 м, Ъ — 528 м, h_x = 280 м, к_г = 340 м, масштаб, плана 1: 5000. Все линии измерены с ошибкой т = 0,2 мм в масштабе плана.

198. Превышение определено геодезическим нивелированием и вычислено по формуле

h = dctgz + d? + i — l.

Найти среднюю квадратическую ошибку превышения^ если ошибка измерения зенитного расстояния т_г — 5", коэффициент рефракции известен с ошибкой 0,03; расстояние d =? 6 км; влияние ошибок определения остальных компонентов формулы практически незначительно.

Решение.

Так как d и m_h выражаются в линейной мере, необходимо т„ заданную в секундах, выразить в радианной мере (ml/p"). Кроме того, поскольку в геодезических сетях z близко к 90°, можно при­нять sin z = 1. Тогда

199. Решить предыдущую задачу при d, равном 4; 10; 20 км; проанализировать, как влияют ошибки т_г и т_к на точность нивели­рования.

200. Вычислить среднюю квадратическую ошибку М среднего значения расстояния, измеренного в прямом и обратном направле­ниях, если средняя квадратическая ошибка измерения в одном направлении т = 1 м.

Решение. Ответ находят по формуле (VIII.19):

Л/Г ^т 1^М AT

М = —г=г = —— = 0,7 м.
Уп V2

201. Угол измерен тремя приемами. Найти среднюю квадрати­ческую ошибку М вероятнейшего значения этого угла, если средняя квадратическая ошибка измерения угла одним приемом т = 10".

202. Каждое из двух значений превышения, измеренного на станции по черным и красным сторонам реек, получено со средней квадратической ошибкой m_h = 3 мм. Найти среднюю квадратиче­скую ошибку среднего значения превышения.

203. Вычислить среднюю квадратическую ошибку угла, измерен­ного одним полным приемом, если считать, что:

а) полный прием выполняется при двух кругах и угол вычис­
ляется как среднее из полученных значений;

б) в каждом полуприеме (круге) значение угла вычисляется как
разность двух направлений;

в) по каждому направлению делается одно наведение и по два
отсчета (при двух совмещениях изображений штрихов), из которых
выводится среднее;

г) ошибка отсчета по оптическому микрометру т₀ — 1,5". Зри­
тельная труба обеспечивает ошибку наведения т₀ = 5";

д) влияние ошибок внешней среды и других источников ошибок,
не учтенных методикой измерения угла, в расчет не принимается.

Указание. Ошибка угла, измеренного при одном круге,

204. Угол измеряется данным теодолитом одним приемом со средней квадратической ошибкой т = 10". Сколькими приемами следует измерить угол, чтобы среднее значение угла получилось со средней квадратической ошибкой, не превышающей 5"?

SO9I Определить вероятнейшее значение угла, измеренного шестью приемами, и его среднюю квадратическую ошибку (табл. 60).

Пример обработки равноточных измерений дан в табл.61.

Средняя квадратическая ошибка одного измерения

Контроль вычисления [б²]:

[б²] = [еб] = [е²] - -И! = 107 - ~ = 33,5.

 

 

отражателя и обратно. При известной скорости распространения радиоволн с D = ¹l₂tc. Определить, с какой точностью необходимо измерить время t, чтобы получить расстояние порядка 10 км с от­носительной ошибкой 1: 300 000, с я«300 000 км/с.

209. Определить среднюю квадратическую ошибку отдельного
измерения из ряда двойных измерений линии.

Решение: (табл. 63).

Таблица 63

210. При исследовании ошибок совмещения штрихов вертикаль­
ного круга теодолита ОТ-02М взяты отсчеты по оптическому микро­
метру при двух совмещениях изображений штрихов на 16 установках
(табл. 64).

Вычислить среднюю квадратическую ошибку отдельного совме­щения.

211. Для определения длины полевого компаратора расстояние
между закрепленными концами линии измерялось десятикратно
двумя 24-метровыми проволоками. Вычислить среднюю квадрати­
ческую ошибку отдельного измерения по результатам следующих
двойных измерений (табл. 65).

 

216. При выводе формулы средней квадратической ошибки еди­
ницы веса он вычисляется по формуле

Используя это выражение, найти формулу для определения веса превышения при геометрическом нивелировании.

Решение. Обозначив ошибку определения превышения на станции т_ь при п станциях, получим ошибку отметки конечной точки хода т_и = m_h Yⁿ-

Примем за ц ошибку единицы веса ц = m_h Vc_x т. е. ошибку ниве­лирования с станций; подставим т_и и ц:

т\с _с

mfti ⁿ

217. Определить среднюю квадратическую ошибку измерения
одного угла ц, в полигонометрии, если известны невязки w замкнутых
полигонов, состоящих каждый из n_t углов, и число полигонов N.

Решение. Рассматривая угловые невязки как истинные ошибки сумм, имеем

Найдем значение Р. Средняя квадратическая ошибка т суммы п углов будет т = ц У~п. Если принять вес одного угла 1/ц² за еди­ницу, тогда вес суммы п углов

1 11

отсюда

^N '

218. Вычислить среднюю квадратическую ошибку измерения
одного^угла при развитии полигонометрической сети, если получены
следующие невязки^углов в полигонах (табл. 68).

 

Поделиться: