Важной частью при решении задач на прочность и жесткость при изгибе является построение эпюр внутренних усилий – поперечных сил и изгибающих моментов. Основные закономерности поведения эпюр внутренних усилий следующие:
– на участках балки, где нет распределенной нагрузки, эпюра поперечных сил ограничивается прямой, параллельной нулевой линии, а эпюра изгибающих моментов – прямой, наклонной к ней;
– на участках балки с равномерно распределенной нагрузкой эпюра поперечных сил ограничивается наклонной к нулевой линии прямой, а эпюра изгибающих моментов – ветвью параболы, направленной выпуклостью навстречу нагрузке;
– если на участке действия равномерно распределенной нагрузки эпюра поперечных сил не пересекает нулевую линию, то изгибающий момент на этом участке изменяется монотонно, без экстремумов;
– если на участке действия равномерно распределенной нагрузки эпюра поперечных сил пересекает нулевую линию, то в месте пересечения на эпюре изгибающих моментов будет экстремум: максимум (поперечная сила меняет знак с плюса на минус) или минимум (поперечная сила меняет знак с минуса на плюс);
– в сечении, где к балке приложена сосредоточенная нагрузка, на эпюре поперечных сил будет скачок, равный величине этой нагрузки;
– в сечении, где к балке приложен внешний сосредоточенный момент, на эпюре изгибающих моментов будет скачок, равный величине этого момента;
– если на участке балки эпюра поперечных сил положительна (отрицательна), то эпюра изгибающих моментов возрастает (убывает) слева направо.
Консольная балка, изображенная на рисунке 8, имеет два участка, различающихся характером нагружения, а следовательно, и законами изменения поперечных сил и изгибающих моментов.
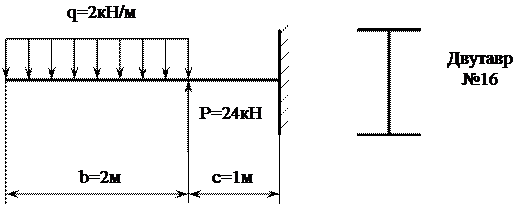
Рисунок 8 – Схема консольной балки
Зададимся системой координат, совместив ось Х с продольной осью балки, а оси У и Z с главными центральными осями инерции поперечного сечения (рисунок 9).
Расчет балки будем вести от свободного конца. В этом случае не потребуется определять опорные реакции в заделке балки. В начале и в конце каждого участка балки проведем характерные сечения и найдем внутренние усилия в этих сечениях, применив правила вычислений и правила знаков для поперечных сил и изгибающих моментов:
;
;
;
;
;
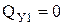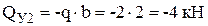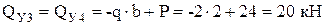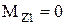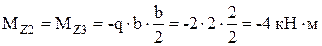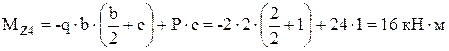
На участке действия равномерно распределенной нагрузки эпюра поперечных сил имеет постоянный знак. Поэтому на этом участке эпюра изгибающих моментов представляет собой ветвь параболы. Вычислим изгибающий момент в дополнительном сечении 5–5, расположенном, например, в середине участка действия равномерно распределенной нагрузки:
.
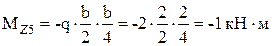По вычисленным значениям строим эпюры внутренних усилий (рисунок 9).
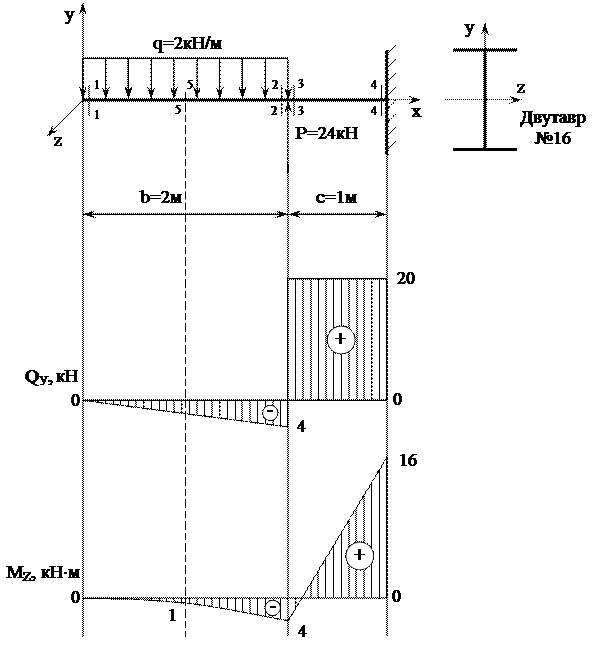
Рисунок 9 – Расчетная схема консольной балки и эпюры внутренних усилий
Условие прочности по нормальным напряжениям при прямом изгибе для балок из пластичных материалов имеет вид:
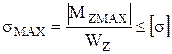, (6)
где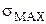 
– абсолютное значение наибольшего нормального напряжения, Па;
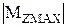– абсолютное значение наибольшего изгибающего момента относительно главной оси инерции Z сечения балки, 
;
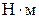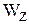– осевой момент сопротивления сечения изгибу относительно главной оси инерции Z сечения балки, м3;
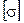– допускаемое нормальное напряжение материала балки, Па.
Опасным сечением консольной балки является сечение 4–4, так как в нем действует наибольший по абсолютному значению изгибающий момент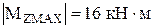 
.
По ГОСТ 8239-89 (Двутавры стальные горячекатаные) найдем, что для двутавра № 16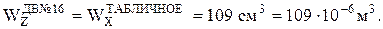 
По условию задачи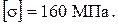 
Определим абсолютное значение наибольшего нормального напряжения в опасном сечении балки:
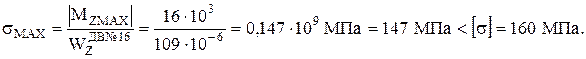Условие прочности выполняется.
Двухопорная балка (рисунок 10) имеет четыре участка. Они различаются характером нагружения и законами изменения внутренних усилий.
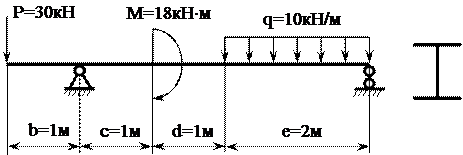
Рисунок 10 – Схема двухопорной балки
Зададимся системой координат, совместив ось Х с продольной осью балки, а оси У и Z с главными центральными осями инерции поперечного сечения (рисунок 11).
Определим опорные реакции. Отбросим опоры А и В и заменим их действие на балку вертикальными составляющими реакци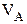й 
и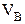 
(горизонтальная составляющая в опоре А равна нулю, так как внешние горизонтальные нагрузки отсутствуют). Составим уравнения равновесия и решим их:
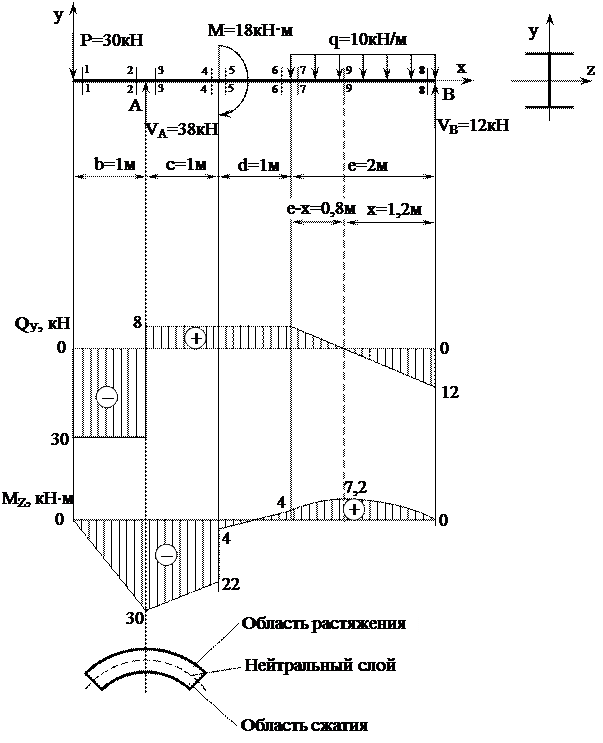
Рисунок 11 – Расчетная схема двухопорной балки и эпюры
внутренних усилий
;
.
;
.
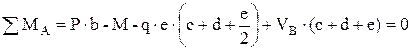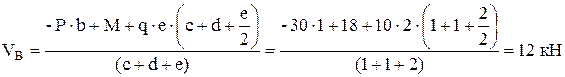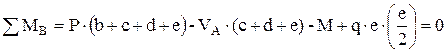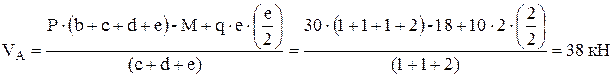Для проверки правильности полученных результатов составим третье уравнение равновесия, спроецировав все силы на ось У:
.
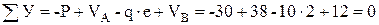Следовательно, опорные реакции найдены верно.
Расчет балки можно вести с любого конца, например, слева направо. В начале и в конце каждого участка балки проведем характерные сечения и найдем внутренние усилия в этих сечениях, применив правила вычислений и правила знаков для поперечных сил и изгибающих моментов:
;
;
;
;
;
;
;
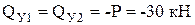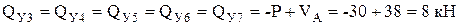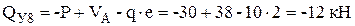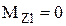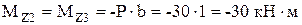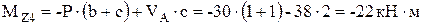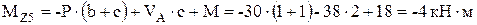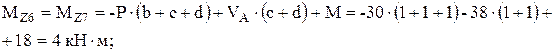
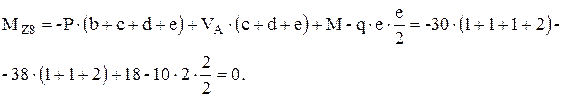
По вычисленным значениям построим эпюры внутренних усилий (рисунок 11). На участке действия равномерно распределенной нагрузки эпюра поперечных сил меняют знак с плюса на минус. Поэтому на этом участке эпюра изгибающих моментов представляет собой ветвь параболы с вершиной в сечении, в котором поперечная сила равна нулю. Из условия подобия треугольников эпюры поперечных сил (рисунок 11) найдем расстояние от сечения 8–8 (опора В) до дополнительного сечения 9–9, в котором эпюра изгибающих моментов достигает максимума на участке действия равномерно распределенной нагрузки:
;
;
.
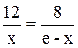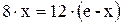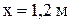Вычислим изгибающий момент в дополнительном сечении 9–9:
.
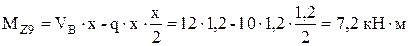Опасными сечениями балки являются сечения 2–2 и 3–3. В них действует наибольший по абсолютному значению изгибающий момент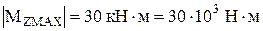 
.
Из формулы (6) определим требуемый для выполнения условия прочности осевой момент сопротивления сечения изгибу относительно главной оси инерции Z сечения балки:
.
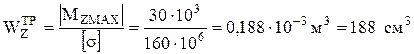Здесь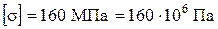 
по условию задачи.
По ГОСТ 8239-89 выберем двутавр № 22 с ближайшим большим моментом сопротивления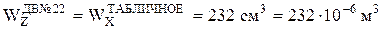 
.
Вычислим абсолютное значение наибольшего нормального напряжения в опасных сечениях балки:
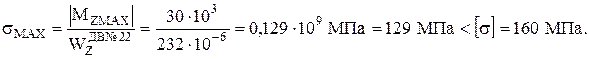
Условие прочности выполняется.
Найдем по формуле (2) коэффициент запаса прочности по отношению к пределу текучести, если по условию задачи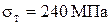 
:
.
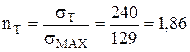Величина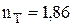 
находится в рекомендуемом от 1,5 до 2,0 диапазоне значений.
Нормальное напряжение в произвольной точке j данного поперечного сечения балки при прямом изгибе определяется формулой:
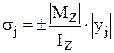, (7)
где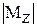 
– абсолютное значение изгибающего момента в сечении балки, ;
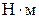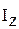– момент инерции сечения относительно главной оси инерции Z сече-
ния балки, м4;
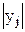– абсолютное значение расстояния от оси Z до точки j, м;
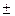– знак напряжения (зависит от того, в какой области сечения находится
точка j – в области растянутых (плюс) или сжатых (минус) слоев ма-
териала балки.
Для построения пространственной эпюры нормальных напряжений в опасном сечении двутавровой балки найдем напряжения в точках сечения, наиболее удаленных от главной оси инерции Z сечения. Такими точками являются все точки верхней (отрезок АВ) и нижней (отрезок DК) границ сечения (рисунок 12).
По ГОСТ 8239-89 для двутавра № 22 расстояние от оси Z (в таблице ось Х) до наиболее удаленных точек сечения составит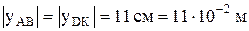 
(половина высоты двутавра).
Там же найдем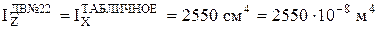 
.
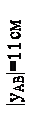
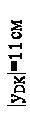
Рисунок 12 – Пространственная эпюра нормальных напряжений
в опасном сечении балки
В данном примере изгибающий момент в опасных сечениях балки отрицательный. По правилу знаков это означает, что в этих сечениях балка изогнута выпуклостью вверх (рисунок 11). Значит, все точки сечения выше оси Z находятся в области растянутых слоев, а ниже оси Z – в области сжатых слоев материала балки. Поэтому в точках отрезка АВ нормальные напряжения положительные, а в точках отрезка DК – отрицательные.
Тогда
;
.
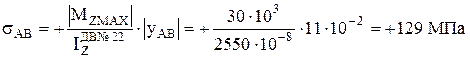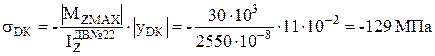Для построения эпюры рассечем балку по опасному сечению, одну из частей отбросим, а другую вычертим в масштабе в аксонометрии (рисунок 12), показав на сечении главные оси инерции Z и У и центр тяжести (точка С). В выбранном масштабе отложим из угловых точек сечения А и В векторы напряжений, направив их от сечения (напряжения растягивающие). Из точек D и К отложим векторы напряжений, направив их на сечение (напряжения сжимающие). Соединим концы векторов, выходящие из точек А и В прямой линией, которая будет ограничивать векторы напряжений в других точках отрезка АВ сечения. Аналогично построим эпюру нормальных напряжений для точек отрезка DК сечения. Также соединим прямой концы векторов, выходящих из точек пересечения отрезков АВ и DК с осью У. Эта прямая ограничит векторы напряжений, действующих в точках оси У сечения балки, и пройдет через центр тяжести сечения С. Соединим прямыми точки А и D и концы векторов, выходящие из этих точек. Точка пересечения этих прямых Е должна лежать на оси Z сечения балки. Аналогичное построение проведем для другой пары точек и векторов. Точка F должна лежать на оси Z. Таким образом, нейтральная (нулевая) линия совпадает с главной центральной осью инерции Z сечения балки.