Перечень вопросов к экзаменационным билетам
1. Высказывания. Основные логические операции. Понятие формулы логики. Построение таблицы истинности для формулы. Условные высказывания.
2. Равносильные формулы. Законы логики. Методика упрощения формул логики с помощью равносильных преобразований.
3. Булевы функции. Законы логики. Решение логических задач с помощью булевых функций.
4. Дизъюнктивная нормальная форма. Методика представления булевой функции в виде СДНФ. Минимизация нормальных форм.
5. Конъюнктивная нормальная форма. Методика представления булевой функции в виде СКНФ. Минимизация нормальных форм.
6. Логические схемы. Минимизация логической схемы.
7. Понятие множества. Количество подмножеств множества. Операции над множествами. Декартово произведение множеств. Диаграммы Венна и круги Эйлера.
8. Исчисление предикатов. Понятие предиката. Область определения и область истинности предиката. Кванторные операции над предикатами. Построение отрицания к предикатам. Диаграммы Эйлера.
9. Кодирование информации. Код с проверкой чётности, код с тройным повторением. Расстояние Хемминга.
10. Шифрование. Основные понятия. Шифры перестановки, замены.
11. Метод математической индукции.
12. Комбинаторика. Сочетания, размещения и перестановки. Сочетания с повторениями. Бином Ньютона.
13. Неориентированные графы. Способы задания. Матрица смежности.
14. Ориентированные графы. Способы задания. Матрицы инцидентности и смежности.
15. Эйлеровы графы. Раскраска графов.
16. Использование диаграмм Эйлера-Вена для иллюстрации операций на множествах.
17. Способы задания отношений на множествах.
18. Основные свойства отношений на множествах.
Перечень практических заданий к экзаменационным билетам
1. Дана функция f(x,y,z)=(z®y¢)×(x¢+z). Требуется:
a. Вычислить значение функции на наборах (0,0,1) и (0,1,0)
b. Найти СДНФ, СКНФ с помощью равносильных преобразований.
2. 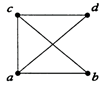 Дан граф. Найдите матрицу смежности и инцидентности графа. Определите, имеет ли граф Эйлеров цикл? Собственный Эйлеров цикл? Найдите все пути длины 2 для графа.
Дан граф. Найдите матрицу смежности и инцидентности графа. Определите, имеет ли граф Эйлеров цикл? Собственный Эйлеров цикл? Найдите все пути длины 2 для графа.
4. Используя метод математической индукции, докажите: 
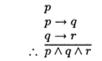 5. Докажите, что умозаключение является верным с помощью:
5. Докажите, что умозаключение является верным с помощью:
a. Построения таблицы истинности
b. Метода равносильных преобразований
6. Дана функция f(x,y,z)=(x×y¢)®(y¢+z). Требуется:
a) Вычислить значение функции на наборах (1,0,0) и (0,1,0)
b) Найти СДНФ, СКНФ с помощью равносильных преобразований.
7. Для заданной булевой функции трёх переменных f(x,y,z)=(x+y¢)¢®(zÅx¢):
а). Постройте таблицу истинности. Найдите СДНФ и СКНФ.
б). С помощью эквивалентных преобразований приведите функцию к ДНФ, КНФ.
Комбинаторика
8. В классе 250 студентов. Из них 130 – изучают историю, 110 – географию, а 80 – и то и другое. Сколько студентов изучают хотя бы один из курсов? Не изучают ни одного из курсов?
9. Для заданной булевой функции трёх переменных f(x,y,z)=(x+y)®(z¢Åx¢):
a) Постройте таблицу истинности. Найдите СДНФ и СКНФ.
b) С помощью эквивалентных преобразований приведите функцию к ДНФ, КНФ.
10. Для каждого из приведённых ниже множеств используйте диаграммы Венна заштрихуйте только те её части, которые изображают заданные множества.
a. (A– B)Ç(A– C)
b. (AÈB) – C
11. Проверьте, имеет ли место равносильность: 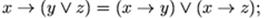
12. Упростите высказывания:
c. (AÚB)Ú(CÙØB)
d. (A∨B) ∧ A
13. Постройте СДНФ и СКНФ по таблице истинности. Упростите с помощью эквивалентных преобразований:
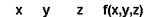
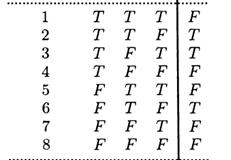
| 17. Запишите приведённые ниже предложения в символической форме, используя предикаты: а). Существуют животные, которые могут обогнать людей. б). Дима – лучший футболист в мире. в). Для каждого действия существует противодействие. |
| 18. Проверьте правильность умозаключения с помощью кругов Эйлера: Все люди – счастливы Все счастливые люди верят в себя Все люди верят в себя |
19. 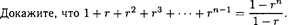
|